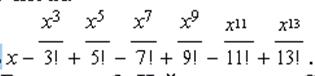Лабораторная работа №13. Циклы и массивы

 

Цель работы: отработка навыков работы с циклами и массивами.

 

13.1 Рабочее задание

 

В Python решить пять задач по вариантам.

Вариант 1.

1) Дан одномерный массив чисел a₁,...,a₂₀. Заполнить его случайным образом и отсортировать.

 

2) Известно, что 1 число - понедельник, тогда каким днем недели будет n-ное число месяца.

 

3) Дано количество дней в месяце. Определить возможный месяц.

4) Дана квадратная матрица. Получить обратную к ней матрицу.

 

5) Дан массив k*k. Заменить элементы главной диагонали на элементы дополнительной диагонали.

 

Вариант 2.

 

1) Найти среднее значение всех элементов одномерного массива, длиной n, заданного случайным образом.

 

2) Задан одномерный массив, длиной k. Найти максимальный элемент массива.

 

3) Вывести массив чисел из 16 первых элементов ряда чисел Фибоначчи в виде квадратной матрицы.

2 0	^x ij
4) Найти å		.
i, j= 1	i

 

5) Дано n. Выяснить, сколько положительных элементов содержит

|а_ij|i,j=1,…n, если а_ij= ^{i 2 - j 2}.

n

Вариант 3.

 

1) Дан массив случайных чисел из а элементов. Вывести на экран только те элементы этого массива, индексы которых кратны трем.

 

2) Если 2-е число месяца – четверг, тогда каким днем недели будет n-ное число месяца.

 

3) Дан массив чисел, заполненный случайным образом. Вывести все элементы массива, индексы которых не меньше k и не больше n.

 

4) Пользователь вводит массив чисел n*n элементов. Записать матрицу

в обратном виде (с конца).

 

5) Вывести двумерный массив n*m, в котором первые элементы числа 3 и 5, а следующие элементы формируется путем сложения предыдущих двух и деления их на 2.

 

Вариант 4.

20 _x

1) Пусть х₁=х₂=х₃=1; x_i= x_i-1+x_i-3; i=4,5,… Найти å ⁱ.

_{i =1} 2 ⁱ

 

2) Дан массив случайных чисел n элементов. Поменять симметрично местами (первый с последним, предпоследний со вторым и т.д.).

 

3) Дан массив случайных чисел из n элементов. Вывести числа, в индексе которых есть число 2.

 

4) Вводится матрица n*n. Cтоящие выше строки k обнулить, нижестоящие элементы - отсортировать по убыванию.

 

5) Даны число n, матрица 4*4. Найти среднее геометрическое главной диагонали и заменить им максимальный элемент побочной диагонали, положительные элементы матрицы обнулить, остальные не менять.

 

Вариант 5.

 

1) Отсортировать все элементы массива, введенные случайным образом (n - колиество элементов массива) по возрастанию.

 

2) Дан массив чисел, вводимых пользователем из n элементов. Составить второй массив из чисел, в индексе которых есть число 2. Отсортировать все числа по убыванию в полученном массиве.

 

3) Найти среднее геометрическое всех элементов одномерного массива, длиной n, заданного случайным образом.

 

4) Дана квадратная матрица. Получить обратную к ней матрицу, умноженную на транспонированную.

 

5) В массиве случайных чисел m*m. Заменить элементы первых n строк на 1, элементы 2-х следующих строк поменять симметрично построчно местами (первый с последним и т.д.), остальные обнулить.

 

Вариант 6.

 

1) Вывести все нечетные элементы массива, делящиеся на 3, введенного вручную из n элементов.

 

2) Вывести массив чисел из 25 первых элементов ряда чисел Фибоначчи.

 

3) Дан массив случайных чисел из n элементов. Построить новый массив чисел, содержащий в индексе единицу или двойку. Отсортировать полученный массив по убыванию.

 

4) Дана матрица, номера k, n, h. Поменять местами между собой элементы строчек с этими номерами.

 

5) Из матрицы А случайных чисел вывести матрицы: В – элементы верхней диагональной матрицы, С – элементы нижней матрицы.

 

Вариант 7.

 

1) Если 2-е число месяца – суббота, тогда каким днем недели будет n-ный понедельник месяца.

 

2) Дан массив случайных чисел n элементов, поменять соседние элементы (1-ый элемент с 2-ым, 2-ой с 3-им, …, последний с 1-ым).

128		1
3) Вычислить: å					.
		(2 i)		2
i =1

4) Дана квадратная матрица А. Получить А³.

5) Матрица 5*6, заменить элементы с нечетными индексами на сумму элементов в строчке, стоящих до этого элемента.

Вариант 8.

 

1) Вывести все четные элементы массива, делящиеся на 4, введенного вручную из n элементов.

 

2) Дана некоторая последовательность случайных чисел длиной n. Разделить список на k (k<4) частей и отсортировать каждую часть. Вывести результат.

 

3) Задана последовательность чисел длиной n. Получить еще 2 последовательности: первая - квадраты соответствующих элементов, а вторая составлена из кубов нечетных элементов.

4) Даны действительные числа а₁, …, а_n. Получить n*m, где m-тая строка есть m-тая степень соответствующего элемента a_i, m=1, …, 5.

 

5) Разбить матрицу на равные части по вертикали.

 

Вариант 9.

 

1) Вывести максимальное произведение из всевозможных комбинаций по 2 числа из k чисел.

 

2) Дано 10 двузначных чисел. Определить максимальное из отношений соседних элементов.

 

3) Посчитать расстояние между k точками, заданными в координатной форме. Сравнить.

 

4) Дана прямоугольная матрица А. Получить транспонированную матрицу.

 

5) А-квадратная матрица. А* - транспонированная. Получить АА*.

Вариант 10.

1) Дано количество дней в месяце. Определить возможное время года.

2) Дан массив случайных чисел длиной n. Отсортировать массив и

 

среднее арифметическое между максимальным и минимальным элементами, записать в виде нового массива.

 

3) Дано 10 двузначных чисел. Отсортировать массив по убыванию.

 

4) Вывести массив чисел 15 первых элементов ряда чисел Фибоначчи в виде прямоугольной матрицы.

 

5) Вывести двумерный массив n*m, в котором первые элементы числа 1

 

и 2, а следующие элементы формируются путем сложения предыдущих 2 и деления их на 2.

 

Вариант 11.

 

1) Дано натуральное число n. Вычислить произведение первых n

 

сомножителей ²₃ * ⁴₃ * ₅⁴ * ⁶₅ * ₇⁶ *...

 

2) Дана последовательность длиной n. Вычислить через какое количество чисел повторяется число k.

 

3) Даны квадратные матрицы А и В порядка n. Получить матрицы АВ+ВА-А.

 

4) Даны матрицы А и В одинаковой размерности, составленные из случайных чисел. Вывести матрицы С, D на основе матриц А и В, таким образом, чтобы матрица С состояла из элементов суммы соответствующих элементов матриц А и В. D=А·А*-В·С. А* - транспонированная.

 

5) Дана квадратная матрица порядка n, заполненная случайными элементами. Присвоить элементам, находящимся выше главной диагонали значение на единицу больше, главную диагональ обнулить, а значение оставшихся элементов умножить на число n.

 

Вариант 12.

1) Даны натуральные числа a₁, b₁, c₁, a₂, b₂, c₂, которые указывают 2 даты (число, месяц, год). Вычислить количество дней, прошедших между двумя этими датами и целое число лет.

 

2) Даны 2 массива чисел по n элементов в каждом, заданные случайным образом. Умножить соответствующие элементы обоих массивов и отсортировать по убыванию.

 

3) Даны 6 массивов случайных чисел из k элементов. Найти среднее арифметическое каждого из массивов и вывести его с индексом того массива, среднее арифметического которого меньше остальных.

 

4) Дана прямоугольная матрица случайных чисел. Заменить все нечетные числа нулями, а четные умножить на 3.

 

5) Дана матрица 4*5. Заменить все элементы с нечетными индексами на число 15, а числа с четными индексами заменить на нули.

 

Вариант 13.

1) Известен ряд некоторых чисел. Отсортировать ряд по возрастанию.

 

2) По заданному расстоянию и скоростям n машин, определить время нахождения в заезде каждой машины. Вычислить среднюю скорость V и вывести список индексов машин, где превышается V.

 

3) Даны k чисел. Найти такие три числа, чтобы их сумма была равна a. Если таких чисел нет, то сообщить.

 

4) Даны натуральное число n, действительная матрица размером n*9. Найти среднее арифметическое каждого из столбцов, каждого из столбцов.

 

5) Найти среднее значение элементов построчно и по столбцам массива n*n случайных чисел.

 

Вариант 14.

1) Дан массив десятичных чисел. Найти самое приближенное число к

числу n.

 

2) Дана некоторая последовательность случайных чисел длиной n. В последовательности определить количество соседств (идущих подряд) двух положительных чисел; трех отрицательных чисел.

3) Дано действительное x. Вычислить

 

4) Даны две квадратные матрицы А и В порядка 3. Найти матрицу С = (А*В)*А.

 

5) Дана матрица 4*6. Найти количество чисел, в которых есть число 2.

Вариант 15.

1) Даны действительные числа а₁, а₂..., а_m. Известно, что а₁>0, и что

среди а₂,..,а_n есть хотя бы одно отрицательное число. Пусть а₁,а₂..,а_n - членытданной последовательности, предшествующей первому отрицательному члену (n-заранее известно). Получить среднее геометрическое а₁,...,а_n.

 

n		x
2) Найти å				i			.
	1 +			y i
i =1

 

3) Даны целые числа m, a₁, a₂,...a₂₀. Найти среди них три натуральных числа i, j, k, каждое из которых не превосходит 20, такие, что a_i+a_j+a_k=m. Если таких чисел нет, то сообщить об этом.

 

4) Дана матрица размером n∙m. Найти среднее арифметическое каждого из столбцов, имеющих 4 номер.

 

5) Дана квадратная матрица размера n*m, в которой не все элементы равны нулю. Получить новую матрицу путем деления всех элементов данной матрицы на ее наибольший по номеру элемент.

Вариант 16.

 

1) Дана последовательность случайных чисел длиной n. Выбросить из ряда те элементы, значение которых равно a и b. Вывести полученное, а затем его отсортировать в порядке возрастания величин.

 

2) Получить все сочетания из 10 элементов по 4 элемента в каждом.

 

3) Дано натуральное число n. Вычислить 1∙2+2∙3∙4+....n(n+1)....2n.

4) Выяснить, сколько положительных элементов содержит матрица

|а_ij|i,j=1,…n, если а_ij=cos(i²+n).

 

5) Дан двумерный массив случайных чисел. Все положительные элементы этого массива заменить на число (-2), нули без изменений, а отрицательные разделить на наибольший элемент массива.

 

Вариант 17.

 

1) Даны 4 массива по 10 элементов, заданные случайно. Сложить соответствующие элементы трех массивов и разделить на соответствующий элемент 4 массива, записать в 5-ый массив, отсортировать по убыванию.

 

2) Дано n, целые a₁,a₂,...a_n. Получить x₁,y₁;x₂y₂;...x_ky_k, где x₁,x₂,...x_m,

 

взятые в порядке следования чётные члены последовательности a₁,a₂,...a_n, а y₁,y₂,...y_l - нечетные члены, k=min(m,l).

 

3) Программа выбирает с помощью датчика случайных чисел четырехзначное число с разными цифрами. Угадать это число. На каждом шаге играющий вводит четырехзначное число, а программа сообщает сколько цифр числа угадано (быки) и сколько угадано на нужном месте (коровы).

 

4) Дан двумерный массив случайных чисел из n элементов. Не меняя структуры, вывести на экран только те элементы этого массива, индексы которых кратны трем, остальные элементы обнулить.

 

5) Дано число n. Выяснить, сколько положительных элементов содержит |а_ij|i,j=1,…n, если а_ij=sin(i+j/2).

 

Вариант 18.

1) Дано натуральное число. Получить все натуральные делители.

 

 

å⁵⁰ 1

2) Вычислить _{i =1 i} 3.

3) Даны действительные числа а₁, а₂..., а_m. Известно, что а₁>0 и что среди а₂,..,а_n есть хотя бы одно отрицательное число. Пусть а₁,а₂..,а_n - члены данной последовательности, предшествующей первому отрицательному члену (n-заранее известно). Получить max(a₁,a₁∙a₂,...,a₁∙a₂...a_n).

 

4) Двумерный массив n∙k. Найти максимальный элемент массива, определить его индекс.

 

5) Дан двумерный массив случайных чисел из n*k элементов. Поменять симметрично построчно местами элементы (первый элемент с последним в той же строке, и т.д..

 

Вариант 19.

1) Даны натуральные числа а1, … а10. Вычислить а1+а22+…+а1010.

2) Матрица А (m*m), число n. Получить матрицу Е+А+А²+…+Аⁿ, где Е

– единичная матрица порядка m.

 

3) Дана матрица 9∙3 случайных чисел. Разбить ее на 3 равные части, вывести и отсортировать по строкам.

 

4) Следом квадратной матрицы называется сумма элементов, расположенных на главной диагонали. Даны квадратная матрица порядка m и натуральное число n. Вычислить следы матриц А, А², …, Аⁿ.

 

5) Дан массив n∙m. Элементы, имеющие в индексе тройку обнулить, остальные оставить без изменения.

Вариант 20.

1) Даны две квадратные матрицы А и В порядка 3. Найти матрицу =

 

А∙В.

 

2) Дана матрица, номера строчек k и n. Поменять местами между собой элементы указанных строчек.

 

3) Дана матрица А случайных чисел. Вывести матрицы В, С на основе матрицы А и строчку чисел, состоящую из элементов, стоящих на главной диагонали: матрица В – элементы верхней диагональной матрицы, матрица С – элементы нижней диагональной матрицы.

		4) Дана квадратная матрица А. Получить А^2.
		5) Получить			матрицу,	элементы	которой	вычисляются
^b ij	=	1		, i, j =1,... n.
		i + j
			-1

Вариант 21.

1) Даны квадратные матрицы А и В порядка n. Получить матрицу АВ-

ВА.

2) Даны квадратные матрицы А, В и С порядка n. Получить матрицу

 

(А+В) ∙С.

 

3) Показать пример разбиения матрицы на 3 части по горизонтали и вертикали.

 

10 15

4) Вычислить å к ³ å(к - а)².

к= 1  а =1

 

5) Дана квадратная матрица порядка n. Получить матрицу В, элементы

	ì 1				приi £ j
	ï
			-1
которой вычисляются по формуле b ij	ï i + j				i, j=,…, n.
	= í	1
	ï				иначе
	ï		-1
	î i + j