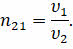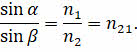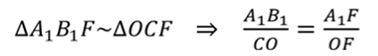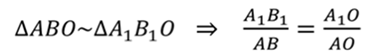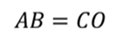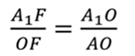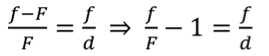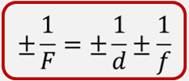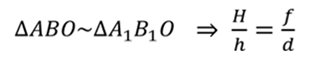Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Преподаватель: Першунина Е.В.Содержание книги Поиск на нашем сайте
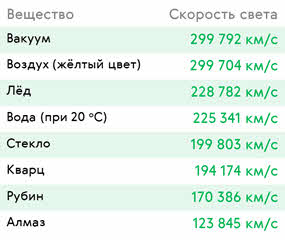
Дисциплина: Физика Преподаватель: Першунина Е.В. Учебный материал на 12, 13 и 15 мая Конспект занятия Оптика Скорость света Почему скорость света является максимальной, конечной и постоянной в нашем мире? Это действительно довольно интересный вопрос, и сразу можно сказать, что ответа на него, в действительности никто точно и не знает почему. Скорость света берется за константу, и на этом постулате, а также на идее о том, что все инерциальные системы отсчета являются равноправными, Альберт Эйнштейн и построил свою специальную теорию относительности, которая вот уже сто лет выводит ученых из равновесия и позволяет Эйнштейну безнаказанно показывать всему миру язык и ухмыляться над размерами той свиньи, которую он подложил всему человечеству.
Но почему же скорость света такая постоянная, максимальная и такая конечная? Ответа так и нет — это аксиома — принятое на веру утверждение, которое подтверждается лишь здравым смыслом и наблюдениями (наподобие того, как через любые две точки можно провести прямую и причем только одну), но никак не логически и не математически выводимое. Если посмотреть в википедии или физическом справочнике, то можно увидеть, что скорость света определена как точное число: 299 792 458 м/с. Ну, если говорить примерно, то это будет 300000 км/с. Встает вопрос, откуда же такая точность? Ведь любая физическая или математическая константа, например число p или основание натурального логарифма e, постоянная Планка или гравитационная постоянная, всегда содержат какие-то цифры после запятой. У p на сегодняшний момент определено около пяти триллионов таких цифр, а постоянная Планка и гравитационная постоянная вообще определяются периодической десятичной дробью.
Но скорость света в вакууме составляет ровно 299 792 458 метров в секунду, ни миллиметром больше, ни наносекундой меньше. Так откуда же такая точность? Началось все как обычно с древних греков. В их времена науки, как таковой в современном ее понимании, еще не было, поэтому они себя называли философами, т.е. они сначала придумывали невероятную теорию у себя в голове, а потом при помощи логических умозаключений пытались эту теорию доказать или опровергнуть.
Первым, кто задумался о том, что у света существует собственная скорость, является философ Эмпидокл, который заявлял, что «свет есть движение, а у движения должна быть скорость». Аристотель же наоборот, говорил, что «свет — это просто присутствие чего-то в природе и все. И ничего не куда не движется».
Птолемей и Евклид вообще считали, что «из глаз выходят чувствительные нити, которые ощупывают своими концами тела и создают зрительные ощущения». Древние греки изощрялись как могли, пока их не завоевали такие же древние римляне. В средневековье, в период господства схоластики и инквизиции, в период рассвета лженаук, заметных исследований по оптике не было, а если и были, то их сожгли. Отметим лишь тот факт, что в этот период, где-то в 1285 году, итальянцем СальвиноД’Армате были изобретены очки для зрения. Поэтому мы опустим данный период.
Далее в западной Европе наступает эпоха Возрождения — период, характеризующийся общим подъемом экономики, культуры, техники и борьбой прогрессивных мировоззрений с схоластикой средневековья. Однако многие ученые все еще продолжают считать, что скорость распространения света бесконечна. Среди них были такие известные ученые как, скажем, Декарт, Кеплер и Ферма.
Но некоторые, например Галилей, верили, что свет обладает конечной скоростью. Галилей даже пытался измерить ее.
Его опыт был достаточно примитивен, однако заслуживает нашего внимания, так как это были первые попытки измерения скорости света. Галилей вместе со своим помощником брали в руки лампы и расходились в разные стороны на несколько километров друг от друга. Далее Галилей зажигал свою лампу и светил ее в сторону помощника. Увидев свет, помощник зажигал свою лампу, и Галилей пытался измерить задержку между данными моментами. Конечно же у него ничего не получилось, и в конце концов он написал в своих сочинениях: «Если у света и есть скорость, то она чрезвычайно велика, а посему можно считать ее бесконечной». В дальнейшем, Рене Декарт одним из первых предложил использовать для измерения скорости света огромные расстояния (например, астрономические), на преодоление которых свету потребуется значительное время. Исторически первое экспериментальное определение скорости света в вакууме в 1676 году предпринял датский астроном Олаф Рёмер. К этому времени почти все астрономы были вооружены телескопами того самого Галилея, и с завидным постоянством наблюдали за четырьмя спутниками Юпитера — Ио, Европой, Каллисто и Ганимедом. Они даже определили примерный период вращения ближайшего к Юпитеру спутника — Ио, который составил около 42-х часов.
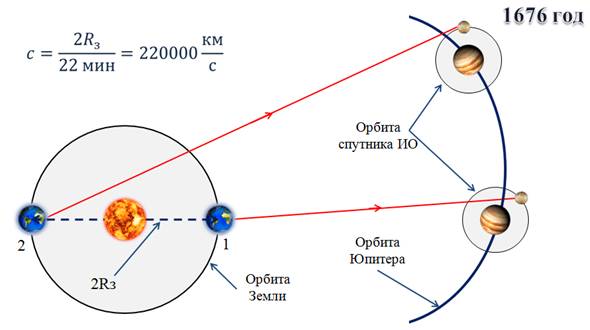
Рёмер, как и все ученые, также наблюдал за этим спутником и, примерно через полгода после начала наблюдений, обнаружил странную вещь. Оказалось, что момент затмения Ио запаздывает относительно вычисленного почти на 11 минут. Дальнейшие его наблюдения показали, что иногда Ио появляется с запаздыванием, а иногда с опережением, но всегда на 11 минут. Рёмер объяснил это опоздание конечностью скорости распространения света. Он рассуждал так: поскольку за полгода Земля переместилась из положения 1 в положение 2, то надо учитывать время, необходимое для того, чтобы свет прошел добавочное расстояние, примерно равное диаметру земной орбиты, а в те времена он уже был более-менее известен. Так вот, просто поделив диаметр Земли на 22 минуты Рёмер получил, что скорость света составляет 220 000 км/с, примерно на треть не досчитавшись до истинного значения.
После Рёмера, а точнее в 1729 году, английский астроном Джеймс Брэдли, наблюдая за звездой гамма-дракона (Этамин), заметил, что данная звезда изменяет свое положение на небосклоне из-за движения Земли вокруг Солнца (эффект аберрации). Бредли решил, что из данного эффекта также можно вычислить скорость света. Сделав необходимые математические вычисления, он получил, что скорость света составляет примерно 301 000 км/с, что уже в пределах точности 1% от известной нам сегодня величины.
В те времена существовало две различные теории о том, что такое свет, которые возникли практически одновременно. Первая теория, именуемая корпускулярной теорией света, связана с именем небезызвестного нам Исаака Ньютона, который считал, что свет — это поток частиц, идущих во все стороны. Вторая теория света, волновая, была разработана Гюйгенсом, который считал свет волной, которая распространяется в какой-то гипотетической среде — светоносном эфире, который заполняет все пространство и проникает во внутрь любых тел. И обе этих теории существовали довольно длительное время. И лишь авторитет Ньютона позволял переманивать ученых на сторону корпускулярной теории. Эта неоднозначность в выборе теории света связана с тем, что известные в то время законы распространения света могли объясняться обеими теориями. Например, прямолинейное распространение света и образование резкой тени за предметами, можно объяснить только на основе корпускулярных взглядов, согласно которым прямолинейное распространение света является просто следствием из закона инерции.
Но в тоже время, корпускулярная теория не могла объяснить, почему тогда световые пучки, пересекаясь в пространстве, не рассеиваются, а продолжают независимое движение. Волновая же теория это легко объясняла.
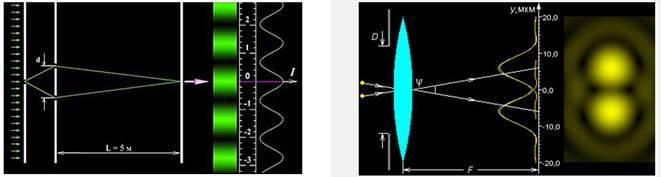
Однако в начале 19 века все меняется — открываются два новых световых явления, которые присущи только волновым процессам — дифракция и интерференция. Первое состоит в том, что свет способен огибать препятствия, соизмеримые с длиной волны, а второе — в явлении усиления или ослабления света при наложении световых пучков друг на друга.
Казалось бы, победа сторонников волновой теории уже близка. Тут еще и Максвелл публикует свою теорию электромагнетизма, в которой указывает на то, что свет является частным случаем электромагнитной волны. А после обнаружения Герцем этих самых волн, вообще не остается никаких сомнений в том, что свет имеет электромагнитную (а значит и волновую) природу. Теперь, сторонники электромагнитной природы света из уравнений Максвелла могли легко посчитать значение скорости света из значений электрической и магнитной проницаемости среды, что и было сделано в 1907 году, уточнив значение скорости света до 299 788 км/с. Но не все так просто в мире физики. В начале 20 века опять меняется представление о природе света. Оказалось, что отвергнутая корпускулярная теория имеет право на жизнь, ведь, например, при излучении или поглощении свет ведет себя подобно потоку частиц, что и продемонстрировал Лебедев в своих опытах с крутильными весами. Возникла необычная ситуация: с одной стороны явления интерференции и дифракции по-прежнему можно объяснить только на основе волновых представлений о свете, а явления излучения и поглощения света только на основе корпускулярных. Поэтому, было решено в одних случаях рассматривать свет, как поток частиц, а в других — в виде электромагнитной волны. В настоящее время это называется корпускулярно-волновым дуализмом. В 1905 году Альберт Эйнштейн создает свою специальную теорию относительности, где заявляет, что скорость света в вакууме — это константа и не зависит вообще ни от чего. Наоборот, все в мире относительно, а скорость света и есть та величина, относительно которой относительны все остальные вещи в нашем мире. Однако точно определить скорость света все еще не могли. И весь 20 век ученые продолжали искать цифры после запятой в значении скорости света. Здесь стоит обратить внимание на опыт американского физика Альберта Абрахама Майкельсона, который для более точного измерения скорости света использовал вращающуюся призму.
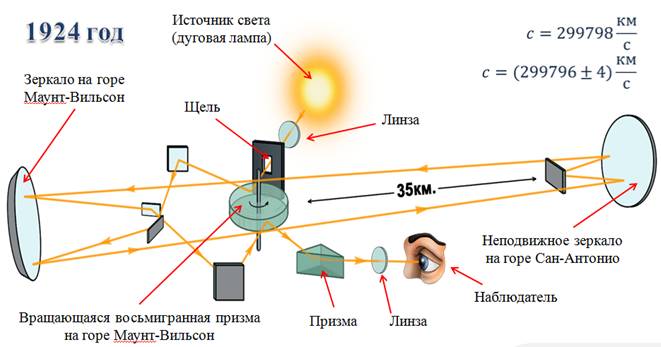
В 1924–1927 годах Майкельсон разработал схему, в котором луч света посылался с вершины горы Вильсон на вершину Сан-Антонио (расстояние порядка 35 км). В качестве вращающегося затвора было использовано вращающееся зеркало, изготовленное с чрезвычайной точностью и приводимое в движение специально разработанным высокоскоростным ротором, делающим до 528 оборотов в секунду. Изменяя частоту вращения ротора, наблюдатель добивался возникновения в окуляре устойчивого изображения источника света. Знание расстояния между установками и частоты вращения зеркала позволяли вычислить скорость света. Начиная с 1924 года и до начала 1927 года было проведено пять независимых серий наблюдений, повышалась точность измерения расстояния и частоты вращения ротора. Средний результат измерений составил 299 798 км/с. Результаты же всех измерений Майкельсона можно записать как 299796 ± 4 км/с.
В 1975 году Генеральная ассамблея мер и весов рекомендовала использовать в качестве значения скорости света в вакууме величину, равную 299 792 458 м/с, с абсолютной погрешностью ± 1,2 м/с. Естественно предположить, что при решении задач по физике, такая большая точность не нужна, и будем пользоваться ее приближенным значением — 3 × 108 м/с. Как оказалось, дальнейшее повышение точности измерений скорости света стало невозможным. Ограничивающим фактором стала величина неопределённости реализации определения метра, действовавшего в то время. Проще говоря, основной вклад в погрешность измерений скорости света вносила погрешность эталона метра. Исходя из этого, а также учитывая другие соображения, XVII Генеральная конференция по мерам и весам в 1983 году приняла новое определение метра, положив в его основу рекомендованное ранее значение скорости света и определив метр как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1/299792458 секунды. В заключение хотелось бы напомнить о том, что было известно о свете раньше из курса физики. При первоначальном ознакомлении с оптическими явлениями в 8 классе было введено понятие светового луча — линии, указывающей направление распространения света, перпендикулярной фронту волны. На основе определения светового луча и строилось изучение геометрической оптики — раздела оптики, в котором изучаются законы распространения света в прозрачных средах и законы его отражения от зеркальных поверхностей. Так же стоит отметить, что одним из основных положений геометрической оптики является положение о прямолинейности распространения света. Законы преломления света С помощью простых опытов мы показали, что в однородной среде свет распространяется прямолинейно. Если же пучок света падает на границу раздела двух однородных прозрачных сред, то часть его отражается и возвращается в первоначальную среду. При этом падающий луч, отражённый луч и нормаль к отражающей поверхности в точке падения луча лежат в одной плоскости. А угол отражения равен углу падения. Также мы с вами смогли доказать закон отражения света с помощью принципа Гюйгенса, согласно которому, каждая точка волнового фронта является источником вторичных сферических волн. Огибающая поверхность к фронтам волн от вторичных источников определяет положение нового фронта волны. Однако, свет, падая на границу раздела двух сред, не только отражается от неё, но и частично проходит во вторую среду и распространяется в ней. Явление изменения направления распространения света при его переходе из одной среды в другую называется преломлением света.
Интересно, что первые упоминания о преломлении света в воде и стекле встречаются в труде Клавдия Птолемея «Оптика», вышедшем в свет во II в. н. э.. Давайте вспомним некоторые понятия и законы, связанные с данным явлением. Для этого обратимся к простому опыту: укрепим в центре оптического диска тонкую стеклянную пластинку и направим на неё узкий пучок света. Как видим, небольшая часть света отразилась от пластинки, а часть света прошла сквозь неё, изменив при этом своё направление распространения. Проведём перпендикуляр к границе раздела двух сред в точке падения луча и вспомним, что луч света, идущий к границе раздела двух сред, называется падающим лучом. А угол между падающим лучом и перпендикуляром, восста́вленным в точке падения луча, называется углом падения.
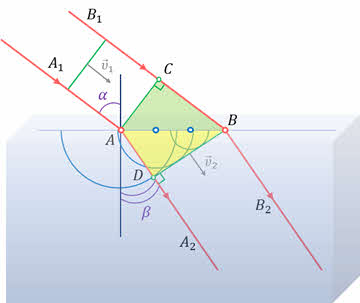
Луч же света, проходящий во вторую среду, называется преломлённым лучом. Следовательно, угол между перпендикуляром, восставленным к границе раздела двух сред в точке падения луча, и преломлённым лучом называется углом преломления. Здесь же отметим, что если свет падает перпендикулярно на границу раздела двух сред, то он не испытывает преломления. Разумеется, не будет преломления и на границе, разделяющей две среды с одинаковыми физическими свойствами. Сравним углы падения и преломления. Как видно, угол преломления меньше угла падения. Увеличим угол падения — угол преломления тоже увеличивается, но по-прежнему он меньше угла падения. А то, что мы на оптическом диске видим не только падающий луч, но и преломлённый, говорит о том, что они оба лежат в одной плоскости — плоскости диска. На основании вышесказанного мы можем с вами сформулировать первую часть закона преломления света. Итак, падающий луч, преломлённый луч и нормаль к границе раздела двух сред в точке падения луча лежат в одной плоскости. Чтобы сформулировать вторую часть закона преломления рассмотрим падение плоской световой волны на плоскую поверхность раздела однородных изотропных и прозрачных сред при условии, что размеры поверхности раздела намного больше длины волны падающего излучения. Если угол падения отличен от нуля, то различные точки фронта волны достигнут границы раздела двух сред не одновременно. Пусть фронт волны перемещается в первой среде со скоростью, модуль которой мы обозначим через υ1. Тогда в точке В колебания начнут возбуждаться с запаздыванием по времени на величину СВ /υ1.
В момент времени, когда волна достигнет точки B и в этой точке начнётся возбуждение колебаний, вторичная волна с центром в точке A уже будет представлять собой полусферу радиусом υ 2Δ t, где υ 2 — это скорость распространения света во второй по ходу луча среде. Радиусы вторичных волн от источников, расположенных между точками A и B, меняются так, как показано на экране. Огибающей вторичных волн является плоскость BD — касательная к сферическим поверхностям. Она представляет собой волновую поверхность преломлённой волны. При этом преломлённые лучи АА 2 и BB 2 перпендикулярны этой поверхности. Давайте посмотрим на Δ АВС — он у нас прямоугольный по построению. Следовательно, угол
Теперь рассмотрим Δ АВD — он тоже прямоугольный по построению. При этом угол
Разделим почленно последние два уравнения друг на друга и упростим полученное равенство:
Отношение
Чем он больше, тем сильнее преломляется свет на границе раздела двух сред.
Таким образом, отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных двух сред, равная относительному показателю преломления второй среды относительно первой:
Это есть вторая часть закона преломления света, экспериментально установленная в 1620 году голландским учёным Виллебродом Снеллом. Однако эти результаты им опубликованы не были. Лишь в 1637 году (уже после смерти учёного) они были обнаружены в архивах математиком Рене Декартом, который использовал их при написании своих «Рассуждений о методе...» в приложении «Диоптрика» (хотя некоторые историки склоняются к тому, что Декарт самостоятельно переоткрыл закон преломления света). Из закона преломления света видно, что различие углов падения и преломления обусловлено тем, что скорость распространения света в различных средах различна. Следовательно, будет различна и длина световой волны. Однако, что очень важно, что при преломлении частота света остаётся неизменной.
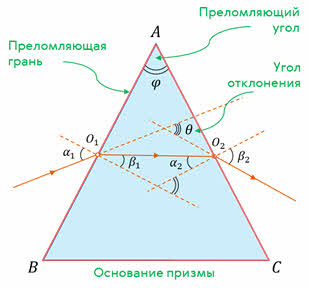
Принято считать, что чем больше скорость распространения света в среде, тем меньше её оптическая плотность и наоборот. При этом если пучок света переходит из среды оптически менее плотной в среду оптически более плотную, то угол преломления меньше угла падения (преломлённый луч как бы прижимается к перпендикуляру). А если свет переходит из среды оптически более плотной в среду оптически менее плотную, то угол преломления больше угла падения (преломлённый луч как бы прижимается к границе раздела сред). Кстати, этот вывод логически следует из свойства обратимости, которое характерно не только для падающего и отражённого, но и для падающего и преломлённого лучей. Если свет падает из вакуума в вещество, то вводится величина, называемая абсолютным показателем преломления. Он показывает, во сколько раз скорость света в вакууме больше, чем в данной среде. С помощью закона преломления света можно рассчитать ход лучей в различных оптических устройствах, например в треугольной призме, изготовленной из какого-либо прозрачного материала. На экране вы видите сечение треугольной стеклянной призмы плоскостью, перпендикулярной её боковым рёбрам. Пусть монохроматический свет (то есть свет строго определённой частоты) падает на грань призмы, находящейся в воздухе. Так как свет переходит из среды оптически менее плотной в оптически более плотную, то угол преломления меньше угла падения. Пройдя через призму, свет падает на её вторую грань. Здесь он снова преломляется, но теперь угол падения меньше угла преломления. Грани, на которых происходит преломление света, называются преломляющими гранями. Угол между преломляющими гранями называется преломляющим углом призмы. Угол, образованный направлением луча, входящего в призму, и направлением луча, выходящего из неё, называют углом отклонения. А грань, лежащая против преломляющего угла, называется основанием призмы.
В заключении отметим, что в настоящее время существуют материалы с отрицательным показателем преломления. Их называют метаматериалами. В большинстве случаев их история начинается с упоминания работы советского физика Виктора Григорьевича Веселаго, опубликованной в журнале «Успехи физических наук» в 1967 году.
Существование подобных материалов было доказано в 2000 году англичанином Джоном Пендри и американцем Дэвидом Смитом. Одно из возможных свойств метаматериалов — это отрицательный (или левосторонний) показатель преломления, который проявляется при одновременной отрицательности диэлектрической и магнитной проницаемостей среды. Линза Нимруда
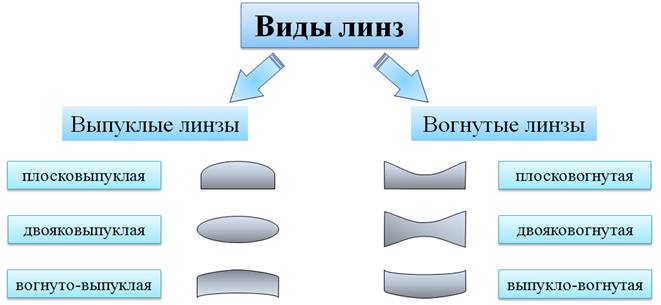
Итак, в современном понимании, линзы — это прозрачные тела, ограниченные криволинейными поверхностями. Чаще всего используются сферические линзы, у которых ограничивающими поверхностями выступают сферы или сфера и плоскость. В зависимости от взаимного размещения сферических поверхностей или сферы и плоскости, различают выпуклые и вогнутые линзы. В свою очередь выпуклые линзы делятся на три вида — плоско выпуклые, двояковыпуклые и вогнуто-выпуклая; а вогнутые линзы подразделяются на плосковогнутые, двояковогнутые и выпукло-вогнутые.
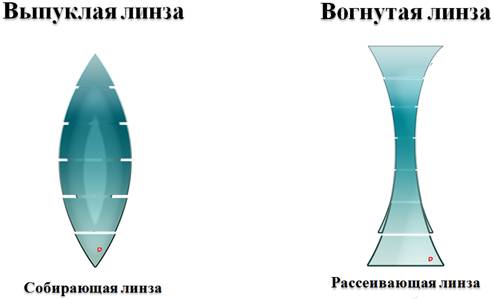
Любую выпуклую линзы можно представить в виде совокупностей плоскопараллельной стеклянной пластинки в центре линзы и усеченных призм, расширяющихся к середине линзы, а вогнутую — как совокупностей плоскопараллельной стеклянной пластинки в центре линзы и усеченных призм, расширяющихся к краям. Известно, что если призма будет сделана из материала, оптически более плотного, чем окружающая среда, то она будет отклонять луч к своему основанию. Поэтому параллельный пучок света после преломления в выпуклой линзе станет сходящимся (такие называются собирающими), а в вогнутой линзе наоборот, параллельный пучок света после преломления станет расходящимся (поэтому такие линзы называются рассеивающими).
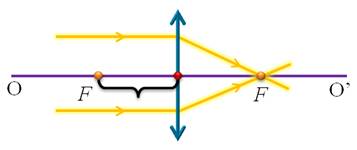
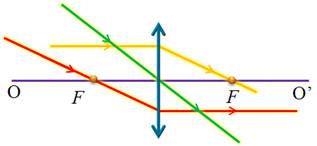
Для простоты и удобства, будем рассматривать линзы, толщина которых пренебрежимо мала, по сравнению с радиусами сферических поверхностей. Такие линзы называют тонкими линзами. И в дальнейшем, когда будем говорить о линзе, всегда будем понимать именно тонкую линзу. Для условного обозначения тонких линз применяют следующий прием: если линза собирающая, то ее обозначают прямой со стрелочками на концах, направленными от центра линзы, а если линза рассеивающая, то стрелочки направлены к центру линзы. Собирающая линза
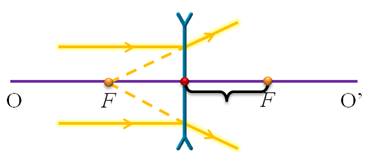
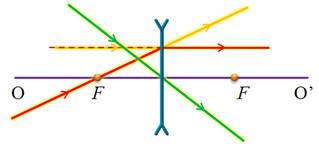
Рассеивающая линза
Расстояние от оптического центра линзы до ее главного фокуса, называется фокусным расстоянием. Фокальная плоскость — это плоскость, перпендикулярная главной оптической оси линзы, проходящая через ее главный фокус. Рассмотрим основные способы построения изображений в тонких линзах. При построении изображений предметов в тонкой линзе мы с вами будем в основном пользоваться тремя «удобными лучами» — это лучи, ход которых после прохождения через линзу нам заранее известен. Собирающая линза
Рассеивающая линза
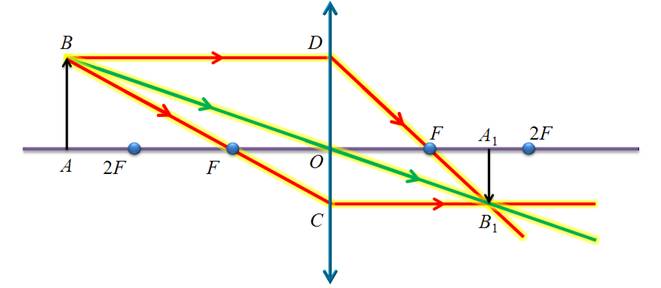
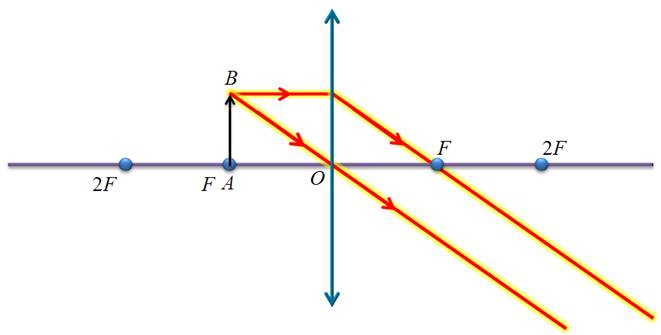
Во-первых, это лучи, идущие параллельно главной оптической оси, т.к. после преломления в линзе, они проходят через ее главный фокус (или проходят их продолжения). Из закона обратимости световых лучей следует, что лучи, которые идут к линзе через ее фокус, после преломления будут направлены параллельно главной оптической оси — это второй набор лучей. И третий набор лучей выбираем исходя из того, что лучи, проходящие через оптический центр линзы, не меняют своего направления. Приступим непосредственно к построению изображений. Для начала рассмотрим собирающую линзу, фокусы и оптический центр которой заранее известны. Для удобства, расстояние от предмета до линзы будем обозначать маленькой латинской буквой d, а расстояние от линзы до изображения — f. Построим изображение плоского предмета AB, находящегося на различных расстояниях от линзы. Для начала рассмотрим случай, когда предмет находится за двойным фокусом линзы. Чтобы построить изображение точки B, направим луч BD параллельно главной оптической оси линзы. После преломления, этот луч, как известно, пойдет через главный фокус линзы. Второй луч BC можно направить через фокус, тогда после преломления в линзе он будет идти параллельно главной оптической оси. В точке пересечения этих двух лучей и будет находиться изображение нашей точки B.
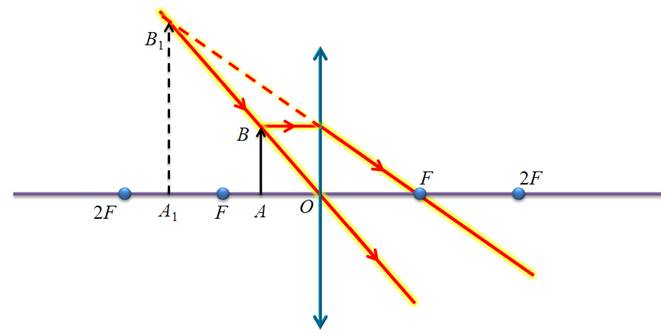
Т.к. наш предмет перпендикулярен главной оптической оси, то теперь достаточно опустить перпендикуляр из точки B 1, чтобы получить вторую точку нашего изображения — точку A 1. Но важно помнить, что так можно делать только тогда, когда предмет перпендикулярен главной оптической оси. Можно было бы использовать и луч BO, проходящий через оптический центр линзы. Таким образом, можно сделать главный вывод о том, что для построения изображения точки достаточно использовать два из трех «удобных» лучей, ход которых через линзу нам заранее известен. Теперь охарактеризуем полученное изображение. Во-первых, оно действительное, так как получилось на пересечении преломленных лучей. Во-вторых, оно перевернутое. В-третьих, как можно видеть из построения, оно уменьшенное. Аналогичным способом, можно построить и охарактеризовать изображение предмета, находящегося на других расстояниях от линзы: Между первым и вторым фокусом
В главном фокусе линзы
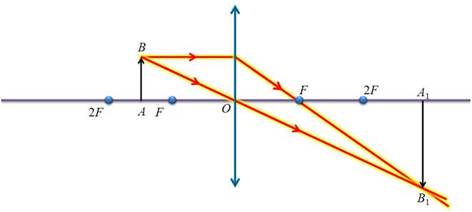
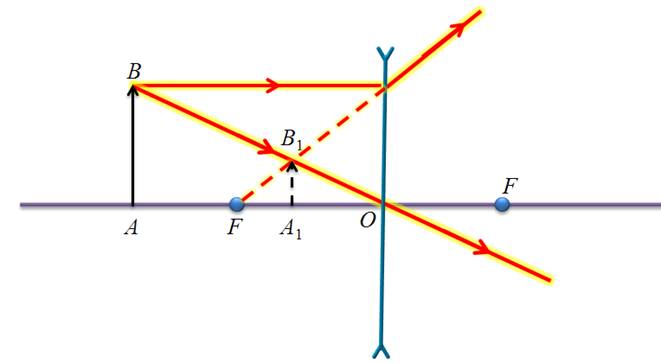
Между фокусом и линзой.
Обратите внимание, что когда предмет располагается между фокусом и линзой, то преломленные лучи расходятся, а пересекаться будут только их продолжения. Поэтому, в этом случае, изображение предмета будет мнимым, увеличенным, прямыми находится со стороны изображаемого предмета. При построении изображения действительного предмета в рассеивающей линзе поступают точно также как и в случае с собирающей. Единственное отличие состоит в том, что у рассеивающей линзы фокус мнимый. Поэтому изображение, даваемое рассеивающей линзой, всегда мнимое, уменьшенное, прямое и находится между линзой и ее фокусом со стороны изображаемого предмета.
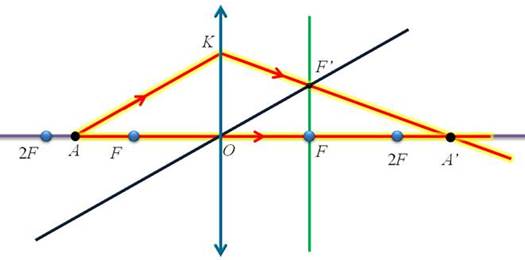
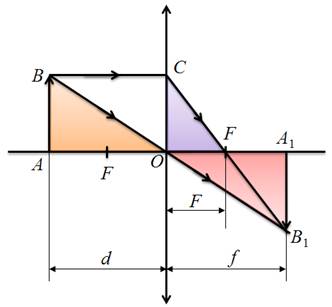
А что делать, если основание предмета находится на главной оптической оси, но сам предмет не перпендикуляре ней? Как строиться изображение в этом случае? Основная трудность заключается в построении изображения точки, являющейся основанием предмета. А дело в том, что все три «удобных» луча будут сливаться в один, который совпадает с главной оптической осью линзы. Для удобства уберем наш предмет, оставив только точку, изображение которой нам надо построить. Чтобы найти, где образуется изображение нашей точки, проведем два луча: первый луч АО, вдоль главной оптической оси (он проходит через оптический центр линзы, не испытывая преломления), а второй луч, например AK, падающий на линзу в произвольной точке K. Здесь главное помнить, что такой луч, после преломления в линзе, не пойдет через ее главный фокус. Для того чтобы найти дальнейший ход этого луча нам необходимо совершить несколько операций.
Во-первых, проведем побочную оптическую ось, параллельную нашему лучу AK. Затем начертим заднюю фокальную плоскость в случае собирающей линзы или переднюю — в случае рассеивающей линзы. Как можно заметить, наша побочная оптическая ось пересеклась с фокальной плоскостью в точке, которую называют побочным фокусом линзы F’. Через этот побочный фокус и пойдут все параллельные побочной оптической оси лучи после преломления в собирающей линзе, или их продолжения в рассеивающей, а следовательно, и наш луч AK. Преломленный луч (или его продолжение) пересечет оптическую ось в точке A 1,которая и является изображением точки А. Выведем формулу, которая свяжет три величины — расстояние от предмета до линзы, расстояние от линзы до изображения и фокус линзы. Рассмотрим собирающую линзу, предмет AB и его изображение в этой линзе A 1 B 1.
Из подобия треугольников
Аналогично, из подобия треугольников
Из построений видно, что
Исходя из этого, можно записать, что
Заменив стороны треугольников через введенные ранее величины, и разделив полученное уравнение на расстояние от линзы до изображения, получим формулу тонкой линзы для рассмотренного случая.
В общем же виде, формула тонкой линзы записывается следующим образом:
Величину, равную обратному фокусному расстоянию линзы, выраженному в метрах, называют оптической силой линзы. Она обозначается большой латинской буквой D и измеряется в диоптриях (сокращенно дптр).
Впервые, полученную нами формулу тонкой линзы, вывел Иоганн Кеплер в 1604 году. Он изучал преломления света при малых углах падения в линзах различной конфигурации. Для практического использования формулы тонкой линзы, нам следует запомнить правило знаков: для собирающей линзы, действительных источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают положительными; для рассеивающей линзы, мнимых источника и изображения, фокусное расстояние, расстояние от предмета до линзы и от линзы до изображения считают отрицательными. Стоит отметить сразу, что предмет или источник является мнимым только в том случае, если на линзу падает пучок сходящихся лучей, продолжения которых пересекаются водной точке. Как можно заметить, чаще всего, изображение, получаемое с помощью тонкой линзы, отличается своими размерами от предмета. Так вот, это различие между размерами предмета и размерами его изображения принято характеризовать линейным (или поперечным) увеличением линзы. Линейное увеличение линзы — это отношение линейного размера изображения к линейному размеру предмета. Обозначается оно большой греческой буквой G.
Если вернуться к рисунку для вывода формулы тонкой линзы, то можно заметить, что
Тогда можно записать, что линейное увеличение линзы равно отношению расстояния от линзы до изображения к расстоянию от предмета до линзы.
Основные выводы: – Линзой называется прозрачное тело, ограниченное криволинейными поверхностями. – Линзы делятся на собирающие и рассеивающие. – Оптическая сила линзы — величина, обратная ее фокусному расстоянию. – «удобные» лучи: луч, проходящий через оптический центр; луч, падающий на линзу параллельно главной оптической оси; луч, проходящий через фокус. – вывели формулу тонкой линзы
Тест 1 Вопрос 1 Показатель преломления стекла больше показателя преломления воды. При переходе из воды в стекло угол преломления Варианты ответов 1. больше угла падении 2. меньше угла падения 3. может быть больше и меньше угла падения, в зависимости от угла падения 4. равен углу падения Вопрос 2 Если луч падает на границу разделе двух прозрачных сред под углом 45°, то угол преломления составляет 60о. Определите по этим данным относительный показатель преломления. (Ответ дайте с точностью до сотых) Вопрос 3 В какой среде свет распространяется с максимальной скоростью? Варианты ответов 1. В слюде 2. В стекле 3. В алмазе 4. В вакууме Вопрос 4 Луч падает на стекло с показателем преломления 1,8 под углом 45о. Найдите угол преломления с точностью до градуса. Вопрос 5 К определениям подпишите понятия Варианты ответов 1. От этого зависит преломляющая способность вещества. 2. Показывает, во сколько раз скорость света в первой по ходу луча среде отличается от скорости распространения света во второй среде. 3. Характеризуется скоростью распространения света в ней. 4. Величина, показывающая во сколько раз скорость света в вакууме больше, чем в данной среде. Вопрос 6 |













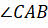 равен углу падения луча АА 1, как углы со взаимно перпендикулярными сторонами. Тогда длину стороны ВС можно найти:
равен углу падения луча АА 1, как углы со взаимно перпендикулярными сторонами. Тогда длину стороны ВС можно найти: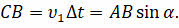
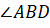 равен углу преломления, как углы между двумя взаимно перпендикулярными сторонами. Поэтому
равен углу преломления, как углы между двумя взаимно перпендикулярными сторонами. Поэтому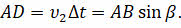
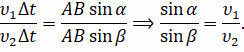
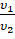 называют относительным показателем преломления. Он показывает, во сколько раз скорость света в первой походу луча среде отличается от скорости распространения света во второй среде:
называют относительным показателем преломления. Он показывает, во сколько раз скорость света в первой походу луча среде отличается от скорости распространения света во второй среде: