
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование рациональных дробейСодержание книги
Поиск на нашем сайте
НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ 1.1. Неопределённый интеграл, его свойства. Определение. Функция Пример. Для функции Теорема (о первообразной для данной функции). Если Доказательство. Пусть Следствие. Если Определение. Неопределенным интегралом от функции
где
вания, Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию. Результат интегрирования можно проверить дифференцированием. Возвращаясь к рассмотренному выше примеру, можно записать: Геометрический смысл неопределённого интеграла от функции Свойства неопределенного интеграла: 1. Действительно, 2. Действительно, 3. 4. 5. Свойство 5 справедливо для любого конечного числа слагаемых. Объединяя свойства 4 и 5, получаем линейное свойство неопределённого интеграла: 6. 7. Теорема (об инвариантности формул интегрирования). Если Доказательство. Так как дифференциал первого порядка обладает свойством инвариантности, то Поскольку операции интегрирования и дифференцирования обратны по отношению друг к другу, то таблица основных интегралов легко получается из таблицы производных. Приведём таблицу основных интегралов для функции Таблица основных интегралов 1. 3. 4. 6. 8. 10. 12. 14. 16. 18. Замечание. Для удобства использования при дальнейшем изложении приведённой таблицы она дополнительно вынесена в Приложение I. Пример. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы:
Решение.
1.2. Замена переменной в неопределённом интеграле Теорема (о замене переменной в неопределённом интеграле). Пусть При этом, если Формула (1) называется формулой замены переменной в неопределенном интеграле. Алгоритм замены переменной в неопределённом интеграле: 1) Связать старую переменную интегрирования 2) Найти связь между дифференциалами: 3) Перейти под знаком интеграла к новой переменной. 4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив Замечание 1. При нахождении дифференциала функций необходимо использовать таблицу производных, поэтому приводим её в Приложении II. Замечание 2. При интегрировании ряда функций часто удобно пользоваться приёмом подведения под знак дифференциала. Проиллюстрируем это на примерах. Пример. Проинтегрировать подходящей заменой переменной или подведением под знак дифференциала.
Решение:
Среди интегралов, вычисляемых с помощью замены переменной, выделим интегралы вида:
При их вычислении необходимо выделить в знаменателе полный квадрат, для чего используется стандартная замена:
Пример. Найти интеграл Решение.
Интегрирование по частям Если функции называемая формулой интегрирования по частям. В качестве Некоторые стандартные случаи функций, интегрируемых по частям, указаны в табл. 1. Там же дается способ выбора множителей Таблица 1
Пример. Проинтегрировать по частям.
Решение.
Решение. а) Подынтегральная дробь неправильная, поэтому выделим целую часть путем деления многочлена на многочлен «углом»:
Итак,
б) Подынтегральная дробь правильная, знаменатель этой дроби разложим на множители, а затем разложим дробь на сумму простейших дробей.
Итак, получаем
Поскольку знаменатели исходной и полученной дробей одинаковы, то приравняем их числители и получим тождество
Сгруппируем в правой части слагаемые с одинаковыми степенями, а затем приравняем коэффициенты при одинаковых степенях x в левой и правой частях тождества:
Следовательно, искомое разложение имеет вид:
Вернёмся к вычислению интеграла:
Решение.
Решение.
Решение.
ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ Формула Ньютона–Лейбница Теорема (о производной от интеграла с переменным верхним пределом). Пусть функция
Доказательство. Обозначим Следствие. Теорема (формула Ньютона–Лейбница). Если функция
где Доказательство. По следствию из предыдущей теоремы
Пример. Вычислить определённый интеграл Решение.
Решение.
Решение.
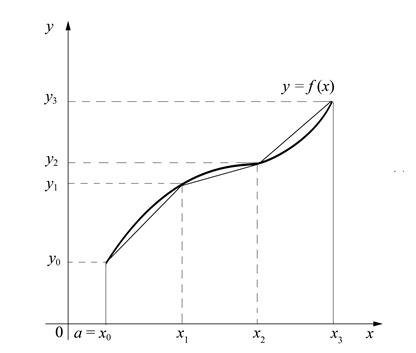
Площади плоских фигур Параметрически Площадь криволинейной трапеции, ограниченной сверху кривой, заданной параметрически уравнениями
Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически: Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра
Нанесём точки (x, y) на координатную плоскость XOY и соединим их плавной линией. Когда параметр
Заметим, что для вычисления площади по формуле (9), построение чертежа не является обязательным, а носит иллюстративный характер. Длина дуги плоской кривой Координатах Если кривая задана уравнением
вычисляется по формуле:
Решение. а) Так как кривая задана в декартовой системе координат уравнением
б) Кривая задана параметрически, поэтому воспользуемся формулой (14). Найдём
Несобственные интегралы Определение. Несобственными интегралами называются интегралы с бесконечными пределами (несобственные интегралы 1-го рода) и интегралы от неограниченных функций (несобственные интегралы 2-го рода). Пусть функция Определение. Если существует конечный предел Геометрический смысл несобственного интеграла Аналогично определяются несобственные интегралы на промежутках
Рассмотрим, как вычисляются несобственные интегралы 1-го рода.
где Аналогично, Пример. Исследовать на сходимость интеграл Решение.
Рассмотрим несобственные интегралы 2-го рода. Пусть функция
При этом несобственный интеграл называется сходящимся, если существуют оба предела в правой части равенства, и расходящимся, если не существует хотя бы один из них. Геометрический смысл несобственного интеграла Пример. Исследовать на сходимость интеграл Решение. Интеграл рода, так как промежуток интегрирования содержит точку бесконечного разрыва
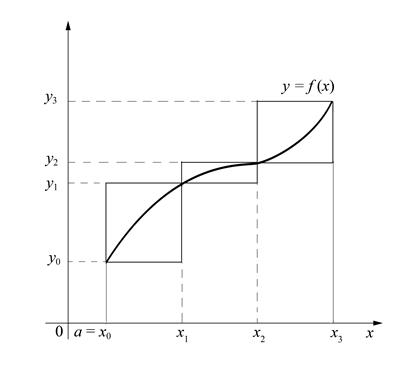
Метод прямоугольников Учитывая геометрический смысл определённого интеграла и заменяя приближённо площади малых криволинейных трапеций площадями соответствующих прямоугольников с теми же основаниями (рис. 7), получаем:
Поскольку все отрезки одинаковой длины, то окончательно имеем:
Формула (17) называется формулой «левых прямоугольников» для приближённого вычисления определённого интеграла. Выбирая прямоугольники другим способом, получим формулу «правых прямоугольников»:
Чем больше число разбиений n, тем точнее приближённое значение определённого интеграла, вычисленного по формулам (17) и (18). Чтобы оценить найденное приближённое значение определённого интеграла, число n отрезков разбиения увеличивают в два раза, сравнивают полученные значения интегралов и оставляют первые совпадающие знаки, если точность недостаточна, то снова удваивают число разбиений и т.д. Отметим, что погрешность R формул прямоугольников оценивается формулой: Метод трапеций Каждую малую криволинейную трапецию приближённо заменим линейной трапецией (рис.8), площадь которой
Поскольку все отрезки одинаковой длины, то окончательно имеем:
Формула (19) называется формулой трапеций для приближённого вычисления определённого интеграла. Для погрешности R формулы (19) справедлива оценка Мы привели только два метода приближённого вычисления определённого интеграла, существуют и другие численные методы вычисления определённых интегралов, учитывающих особенности подынтегральных функций.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Уравнений первого порядка. Линейные уравнения Линейные ДУ 1-го порядка имеют вид:
где p (x) и q (x) — известные функции, непрерывные на некотором интервале. Такие уравнения обычно решают методом Бернулли, который состоит в следующем. Решение ищется в виде произведения двух функций
Объединив второе и третье слагаемые в левой части последнего уравнения и вынося U за скобки, и получим:
Поскольку одну неизвестную функцию у заменили двумя функциями U и V, то одну из этих функций можем взять произвольно. Выберем функцию V (x) так, чтобы она была решением уравнения
тогда вторая функция U (x) должна удовлетворять уравнению
Решив уравнение с разделяющимися переменными (29), найдём V и подставим его в (30), откуда найдём U. Общее решение получим как произведение найденных функций U и V:
Пример. Найти общее решение ДУ Решение. Уравнение имеет вид (27), поэтому является линейным. Решим его методом Бернулли. Сделаем замену
Приравняем коэффициент при U нулю и получим: Решим первое из полученных уравнений:
Полученную функцию
Таким образом, Уравнения Бернулли Уравнения Бернулли имеют вид:
где Метод решения таких уравнений тот же, что и для линейных уравнений. Пример. Найти общее решение ДУ Решение. Разделим уравнение на
Полученное уравнение имеет вид (31), следовательно, это уравнение Бернулли. Сделаем замену
Приравняем коэффициент при U нулю и получим систему уравнений: Решим первое уравнение:
Подставим полученную функцию V во второе уравнение:
Таким образом, общее решение ДУ:
Рассмотрим теперь случаи Все рассмотренные типы ДУ 1-го порядка и методы их решения включены в таблицу ДУ 1-го порядка (см. приложение III).
Решение. а)
б)
Всё изложенное выше применим к случаю ДУ 2-го порядка, как часто встречающемуся и притом весьма важному. Линейные однородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
где р 1 и р 2 — действительные числа. Согласно теореме о структуре общего решения линейного однородного ДУ достаточно найти два линейно независимых частных решения
Будем искать решение уравнения (44) по методу Эйлера. Запишем характеристическое уравнение для ДУ (44):
Корни а) Корни
б) Корни
в) Корни | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: | ||||||||||||||||||||||||||||||||||||||||||||||||||

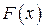 называется первообразной для функции
называется первообразной для функции 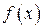 на интервале
на интервале 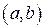 , если для любого
, если для любого 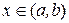 выполняется равенство
выполняется равенство 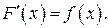
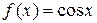 первообразной на множестве всех действительных чисел R =
первообразной на множестве всех действительных чисел R = 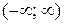 является функция
является функция 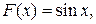 поскольку
поскольку 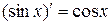 для любого
для любого 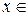 R. Отметим, что первообразными для той же функции
R. Отметим, что первообразными для той же функции 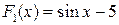 и
и 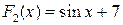 , как и всякая другая функция, отличающаяся от указанных постоянным слагаемым.
, как и всякая другая функция, отличающаяся от указанных постоянным слагаемым.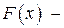 первообразная для функции
первообразная для функции 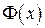 для функции
для функции 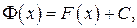 где
где 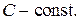
 две первообразные для функции
две первообразные для функции 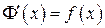 при любом
при любом 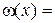
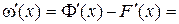
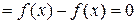 для любого
для любого  , т.е.
, т.е. 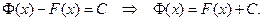
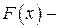 любая первообразная для функции
любая первообразная для функции 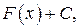 где
где 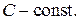
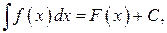
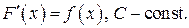 При этом х называют переменной интегриро-
При этом х называют переменной интегриро-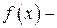 подынтегральной функцией, а
подынтегральной функцией, а 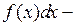 подынтегральным выражением.
подынтегральным выражением.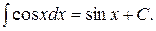
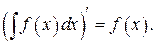
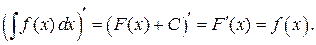
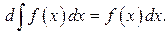
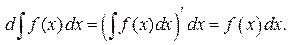
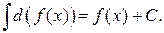
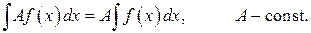
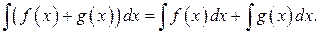
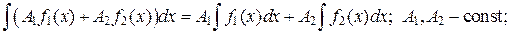
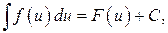 где
где  произвольная непрерывно-дифференцируема функция.
произвольная непрерывно-дифференцируема функция.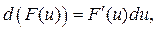 где
где 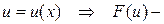 первообразная для
первообразная для 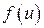 , и, значит
, и, значит 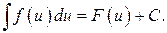
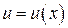 . При этом вместо буквы u при интегрировании может быть использована любая другая буква, например x, t, z и т. д. Кроме формул, получающихся непосредственно из таблицы производных, в таблицу интегралов включено несколько часто встречающихся интегралов.
. При этом вместо буквы u при интегрировании может быть использована любая другая буква, например x, t, z и т. д. Кроме формул, получающихся непосредственно из таблицы производных, в таблицу интегралов включено несколько часто встречающихся интегралов.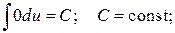 2.
2. 

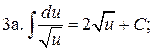
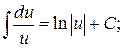 5.
5. 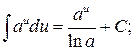
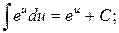 7.
7. 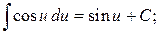
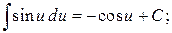 9.
9. 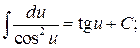
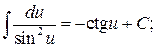 11.
11. 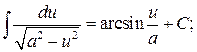
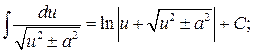 13.
13. 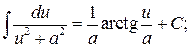
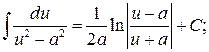 15.
15. 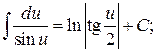
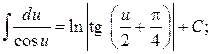 17.
17. 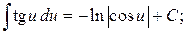
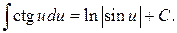
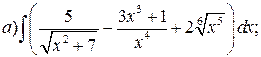
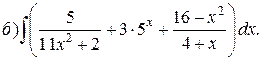
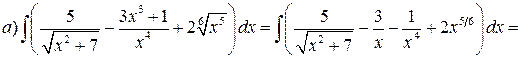
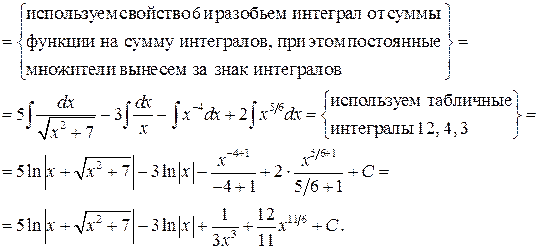
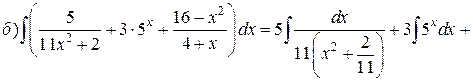
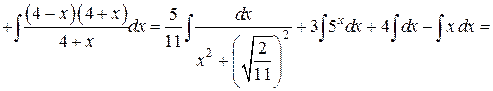
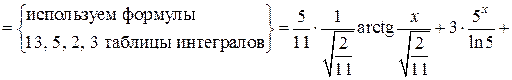
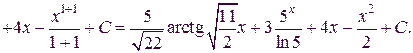
 монотонная, непрерывно-дифференцируемая функция, тогда
монотонная, непрерывно-дифференцируемая функция, тогда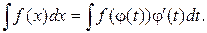 (1)
(1)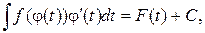 то
то 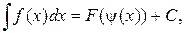 где
где 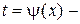 функция, обратная к функции
функция, обратная к функции 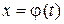 .
.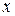 с новой переменной
с новой переменной 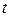 с помощью замены
с помощью замены 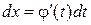 .
.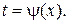
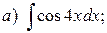
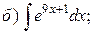
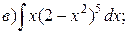
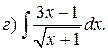
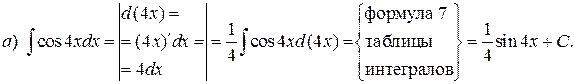
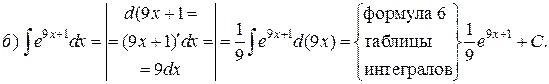

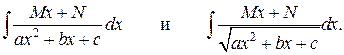
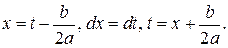 (2)
(2)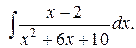
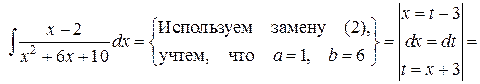
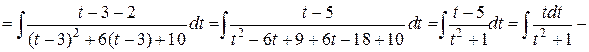
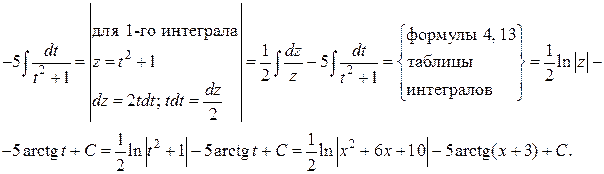
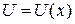 и
и 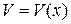 обладают непрерывными производными, то справедлива формула:
обладают непрерывными производными, то справедлива формула:
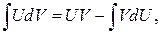 (3)
(3)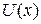 обычно выбирают функцию, которая упрощается при дифференцировании.
обычно выбирают функцию, которая упрощается при дифференцировании.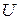 и
и 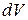 .
.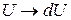
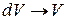

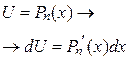
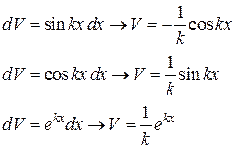

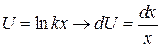
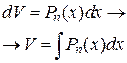
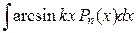
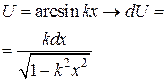
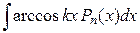
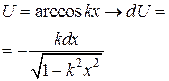
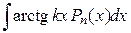
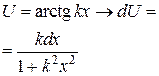
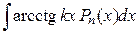
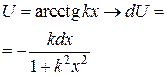
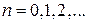
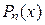 — многочлен от
— многочлен от 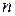 , т. е.
, т. е. 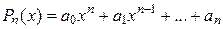 , где
, где  .
.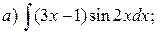
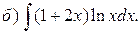
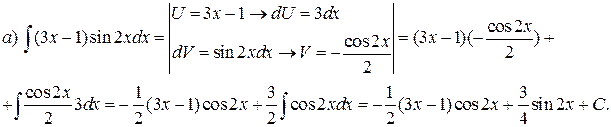
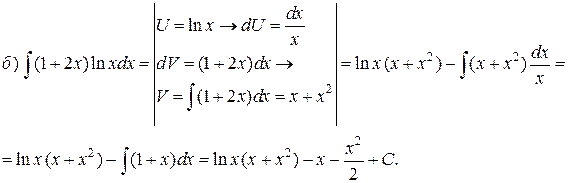
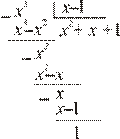
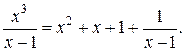 Тогда
Тогда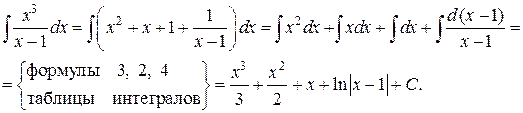
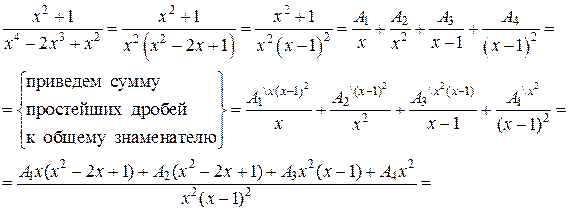
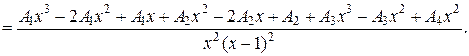
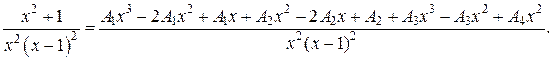
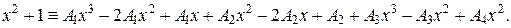
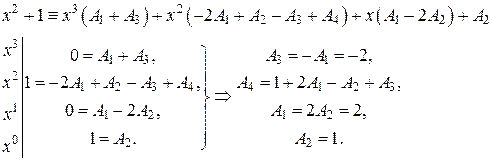
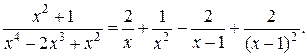
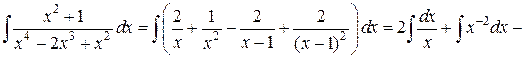

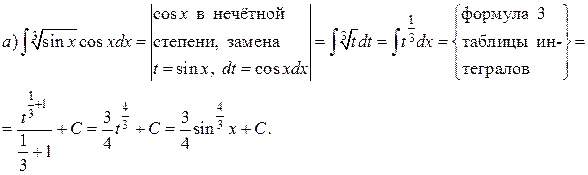
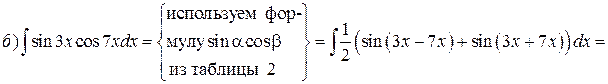
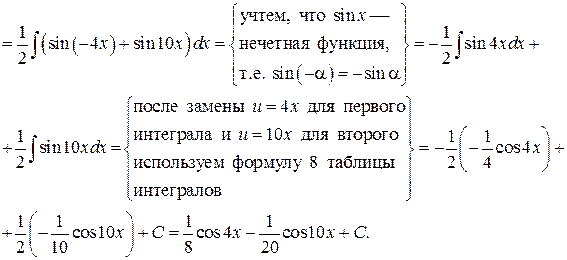
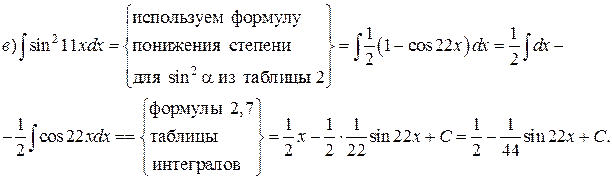
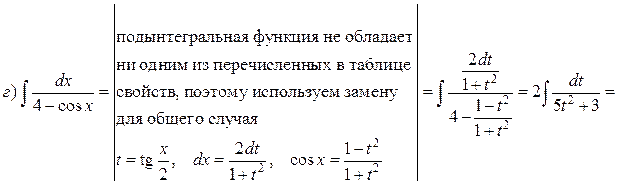
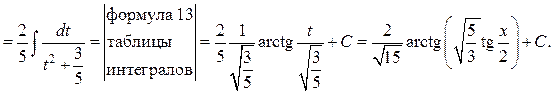
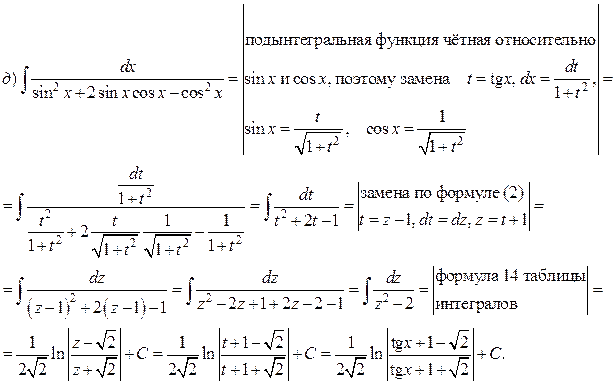
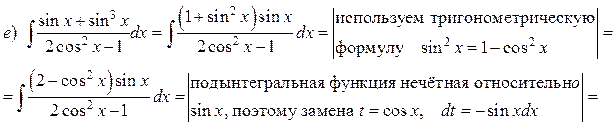
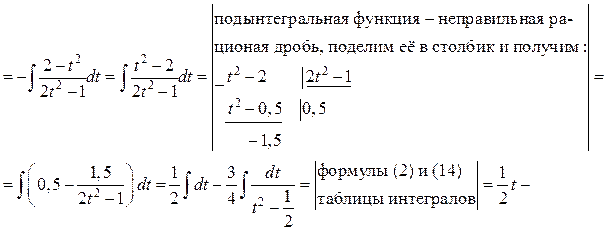
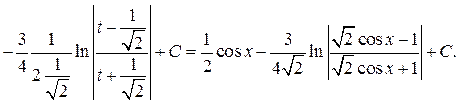
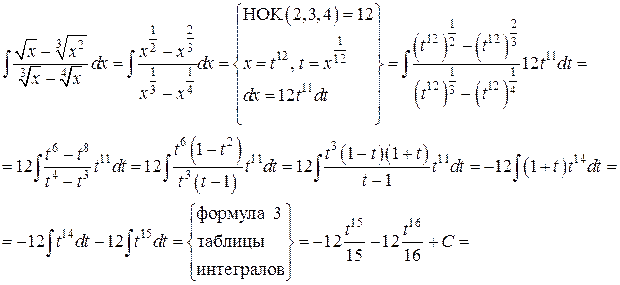
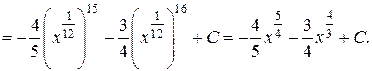
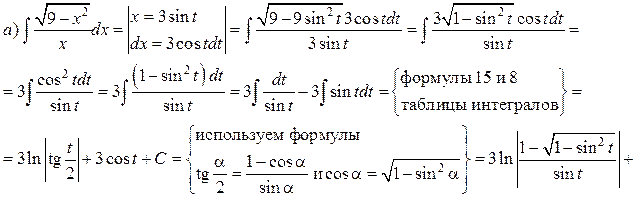
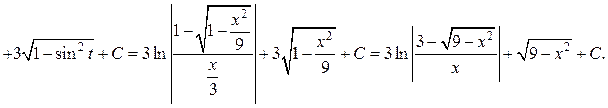
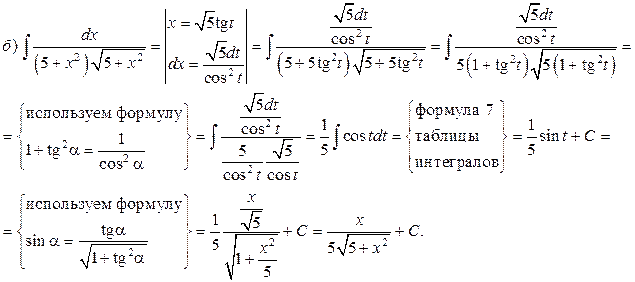
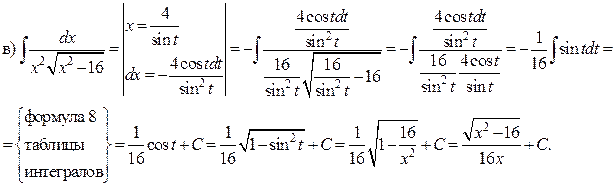
 непрерывна на [ a,b ], тогда производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе:
непрерывна на [ a,b ], тогда производная от определённого интеграла с переменным верхним пределом равна значению подынтегральной функции на этом верхнем пределе: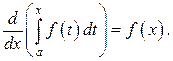
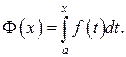 Придадим переменной х приращение
Придадим переменной х приращение 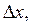 тогда
тогда 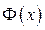 получит приращение
получит приращение 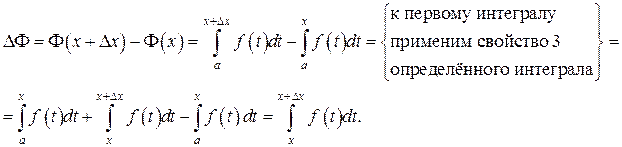
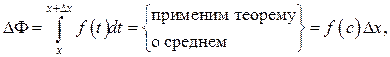 где с – некоторая точка между х и
где с – некоторая точка между х и 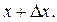 По определению производной имеем
По определению производной имеем 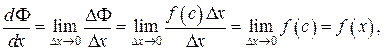 причём последнее равенство справедливо ввиду непрерывности функции
причём последнее равенство справедливо ввиду непрерывности функции 
 первообразная для функции
первообразная для функции  .
.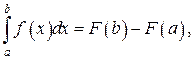 (8)
(8)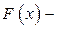 любая первообразная для функции
любая первообразная для функции 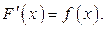
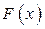 отличается от
отличается от 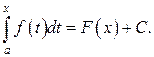 При
При 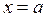 получим
получим 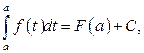 с другой стороны, по свойству 2 определённого интеграла
с другой стороны, по свойству 2 определённого интеграла 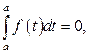 , следовательно,
, следовательно,  и
и  При
При 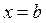 имеем
имеем 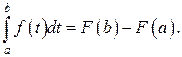
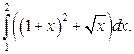
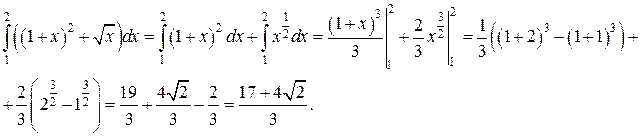
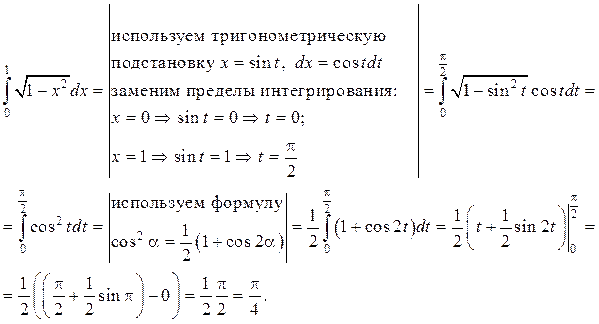
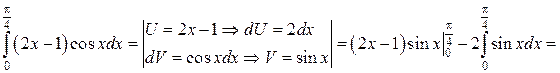
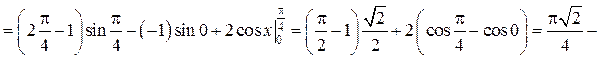
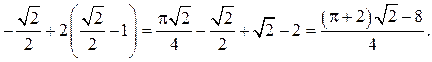
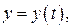
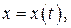 где функции
где функции 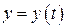 и
и 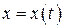 имеют непрерывные производные для всех
имеют непрерывные производные для всех 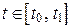 , и функция y (t) сохраняет знак на промежутке
, и функция y (t) сохраняет знак на промежутке 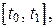 прямыми x = a, x = b, где a = x (t 0), b = x (t 1), и осью OX, вычисляется по формуле:
прямыми x = a, x = b, где a = x (t 0), b = x (t 1), и осью OX, вычисляется по формуле: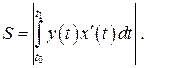 (12)
(12)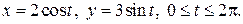
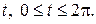
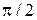
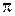
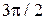

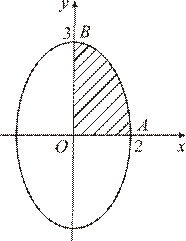
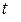 изменяется от
изменяется от 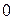 до
до 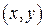 описывает эллипс (известно, что
описывает эллипс (известно, что 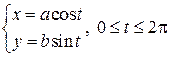 – параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдём её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим:
– параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдём её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (12) получим: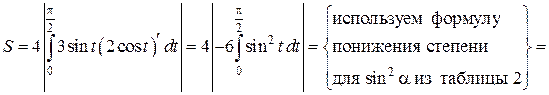
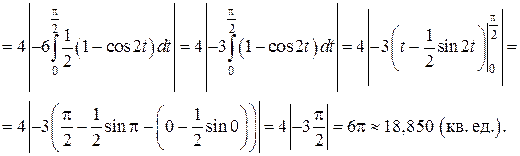
 , функция
, функция 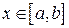 , то длина дуги
, то длина дуги 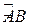 (рис. 4) этой кривой, заключённой между точками
(рис. 4) этой кривой, заключённой между точками 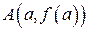 и
и 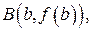
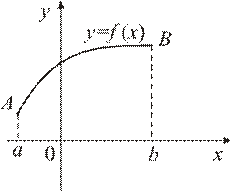
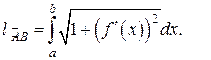 (13)
(13)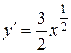 и подставим в (13):
и подставим в (13):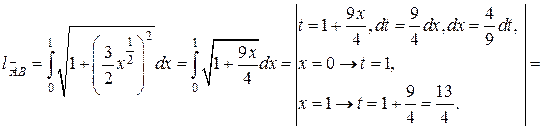
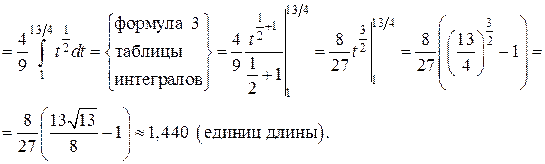
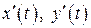 :
: 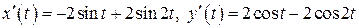 и подставим в (14):
и подставим в (14):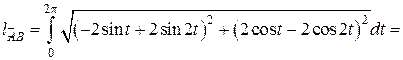
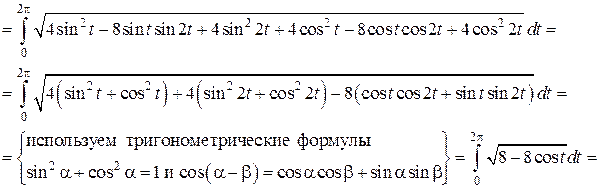
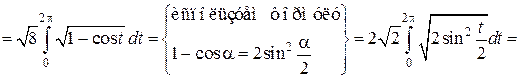
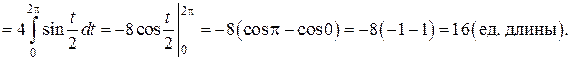
 определена и непрерывна на полусегменте
определена и непрерывна на полусегменте 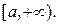 Возьмём любое
Возьмём любое 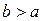 и рассмотрим интеграл
и рассмотрим интеграл 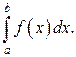
 то этот предел называется несобственным интегралом от функции
то этот предел называется несобственным интегралом от функции 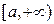 и обозначается
и обозначается 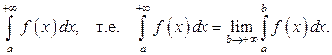 Говорят, что в этом случае несобственный интеграл существует или сходится. Если при
Говорят, что в этом случае несобственный интеграл существует или сходится. Если при 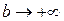 интеграл
интеграл 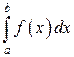 не имеет конечного предела, то говорят, что интеграл
не имеет конечного предела, то говорят, что интеграл 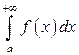 не существует или расходится.
не существует или расходится.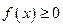 для всех
для всех 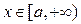 он выражает площадь неограниченной области, заключённой между линиями
он выражает площадь неограниченной области, заключённой между линиями  и осью ОХ.
и осью ОХ.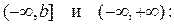
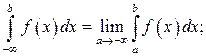
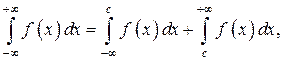 где с – любая точка на интервале
где с – любая точка на интервале 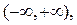 причём
причём 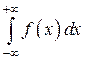 существует, если сходятся оба интеграла в правой части, и расходится, если расходится хотя бы один из них.
существует, если сходятся оба интеграла в правой части, и расходится, если расходится хотя бы один из них.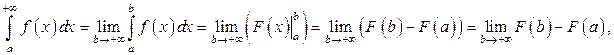
 первообразная для
первообразная для 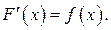
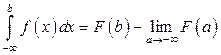 и
и 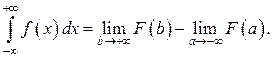
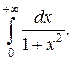
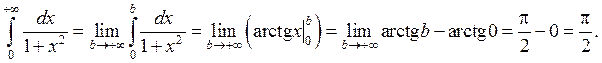 Значит, интеграл сходится и его величина равна
Значит, интеграл сходится и его величина равна 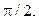
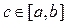 и непрерывна при
и непрерывна при 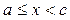 и
и  тогда полагают, что несобственный интеграл определяется формулой:
тогда полагают, что несобственный интеграл определяется формулой: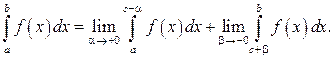 (16)
(16)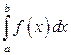 состоит в том, что при
состоит в том, что при 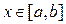 он выражает площадь неограниченной области, заключённой между линиями
он выражает площадь неограниченной области, заключённой между линиями 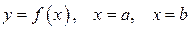 и осью ОХ.
и осью ОХ.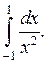
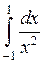 является несобственным интегралом 2-го
является несобственным интегралом 2-го поэтому согласно формуле (16):
поэтому согласно формуле (16):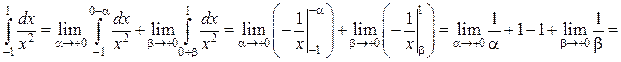
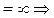 несобственный интеграл расходится.
несобственный интеграл расходится.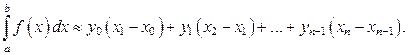
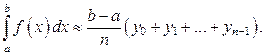 (17)
(17)
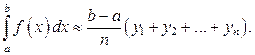 (18)
(18)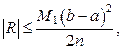 где М 1 – верхняя граница модуля первой производной функции на отрезке
где М 1 – верхняя граница модуля первой производной функции на отрезке 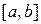 , т.е.
, т.е. 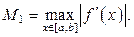
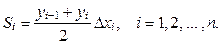 Тогда
Тогда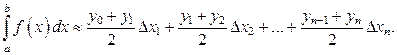
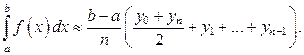 (19)
(19)
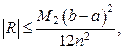 где М 2 – верхняя граница модуля второй производной функции на отрезке
где М 2 – верхняя граница модуля второй производной функции на отрезке 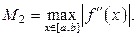
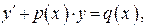 (27)
(27)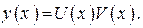 Тогда
Тогда 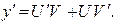 Подставляя y и
Подставляя y и 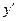 в (5), получаем:
в (5), получаем: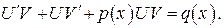
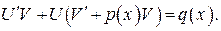 (28)
(28) (29)
(29)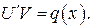 (30)
(30)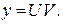
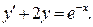
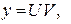
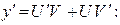

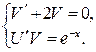
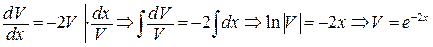 (при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение.
(при интегрировании использовали формулы 4 и 2 таблицы интегралов). При нахождении V постоянную С полагаем равной нулю, так как в данном случае достаточно найти некоторое решение.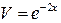 подставим во второе уравнение:
подставим во второе уравнение: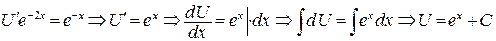 (использовали формулы 2 и 7 таблицы интегралов).
(использовали формулы 2 и 7 таблицы интегралов).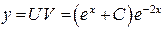 или
или 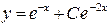 — общее решение исходного ДУ.
— общее решение исходного ДУ.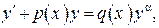 (31)
(31)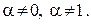
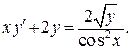
 (х = 0 не является решением данного ДУ):
(х = 0 не является решением данного ДУ):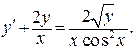
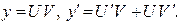 Получим:
Получим: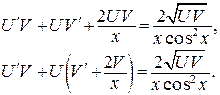
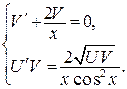
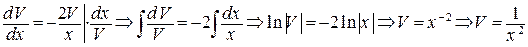 (использовали формулу 4 таблицы интегралов).
(использовали формулу 4 таблицы интегралов).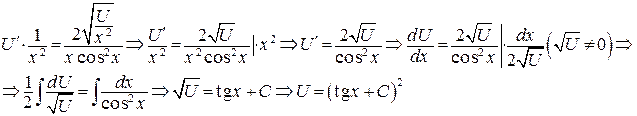 (использовали формулы 3 а и 9 таблицы интегралов).
(использовали формулы 3 а и 9 таблицы интегралов).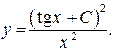
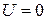 и V = 0, опущенные выше при решении уравнений системы (поскольку выполнялись деления на V и
и V = 0, опущенные выше при решении уравнений системы (поскольку выполнялись деления на V и 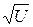 ). В каждом из этих случаев имеем y = 0, что является решением исходного ДУ, и так как это решение не может быть получено из общего решения, то оно является особым решением.
). В каждом из этих случаев имеем y = 0, что является решением исходного ДУ, и так как это решение не может быть получено из общего решения, то оно является особым решением.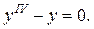 Характеристическое уравнение имеет вид:
Характеристическое уравнение имеет вид:  Оно имеет два различных действительных корня
Оно имеет два различных действительных корня 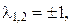 что соответствует случаю 1 и пару комплексно сопряжённых корней
что соответствует случаю 1 и пару комплексно сопряжённых корней 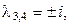 что соответствует случаю 2. Следовательно, общее решение имеет вид:
что соответствует случаю 2. Следовательно, общее решение имеет вид:
 Характеристическое уравнение имеет вид:
Характеристическое уравнение имеет вид: 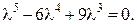 Оно имеет корни
Оно имеет корни 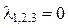 (корень кратности k =3) и
(корень кратности k =3) и 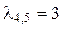 (корень кратности k =2), что соответствует рассмотренному выше случаю 3. Следовательно, общее решение имеет вид:
(корень кратности k =2), что соответствует рассмотренному выше случаю 3. Следовательно, общее решение имеет вид: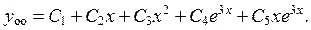
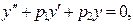 (44)
(44)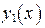 и
и 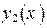 уравнения (44), чтобы записать общее решение:
уравнения (44), чтобы записать общее решение:
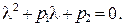 (45)
(45)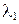 и
и 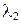 этого квадратного уравнения (с действительными коэффициентам
этого квадратного уравнения (с действительными коэффициентам 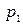 и
и 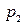 ) могут быть либо действительными, различными или совпадающими, либо комплексно сопряженными. Поэтому согласно сказанному выше, возможны лишь следующие три случая:
) могут быть либо действительными, различными или совпадающими, либо комплексно сопряженными. Поэтому согласно сказанному выше, возможны лишь следующие три случая: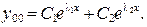 (46)
(46)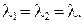 Общее решение уравнения (44) имеет вид:
Общее решение уравнения (44) имеет вид: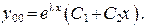 (47)
(47)


