
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Марта 2019 года - остатки Ноу-хау.Содержание книги
Поиск на нашем сайте
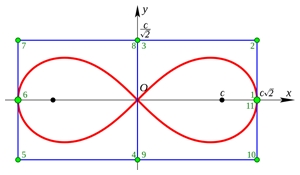
Частицы в МП движутся по траектории "ЛЕМНИСКАТА". Возможно, что надо будет поместить в ЗТР полый замкнутый проводник (ПЗП) и пропустить по нему ток, однонаправленный с током в тороидальных катушках. Форму ПЗП нужно подобрать - это будет или сфероид или эллипсоид или незаконченный в центре лемнискатоид. Тогда ДЗЧ (дейтроны, другие ионы и электроны) будут взаимодействовать с поверхностным током ПЗП по третьему закону Ньютона, что изолирует термоядерную плазму от стенок ПЗП. Стенки ПЗП должны эффективно возвращать в ЗТР все виды излучения. Расчёт внутреннего МП в пристеночном пространстве ПЗП показывает, что ДЗЧ будут "облизывать" стенки ПЗП не прикасаясь к ним. Для полного понимания рекомендую изучить все работы на сайте!!!
Пункты 1-6 подтверждены экспериментами; пункты 7-8 должны быть проверены экспериментами, которые заключаются в следующем:
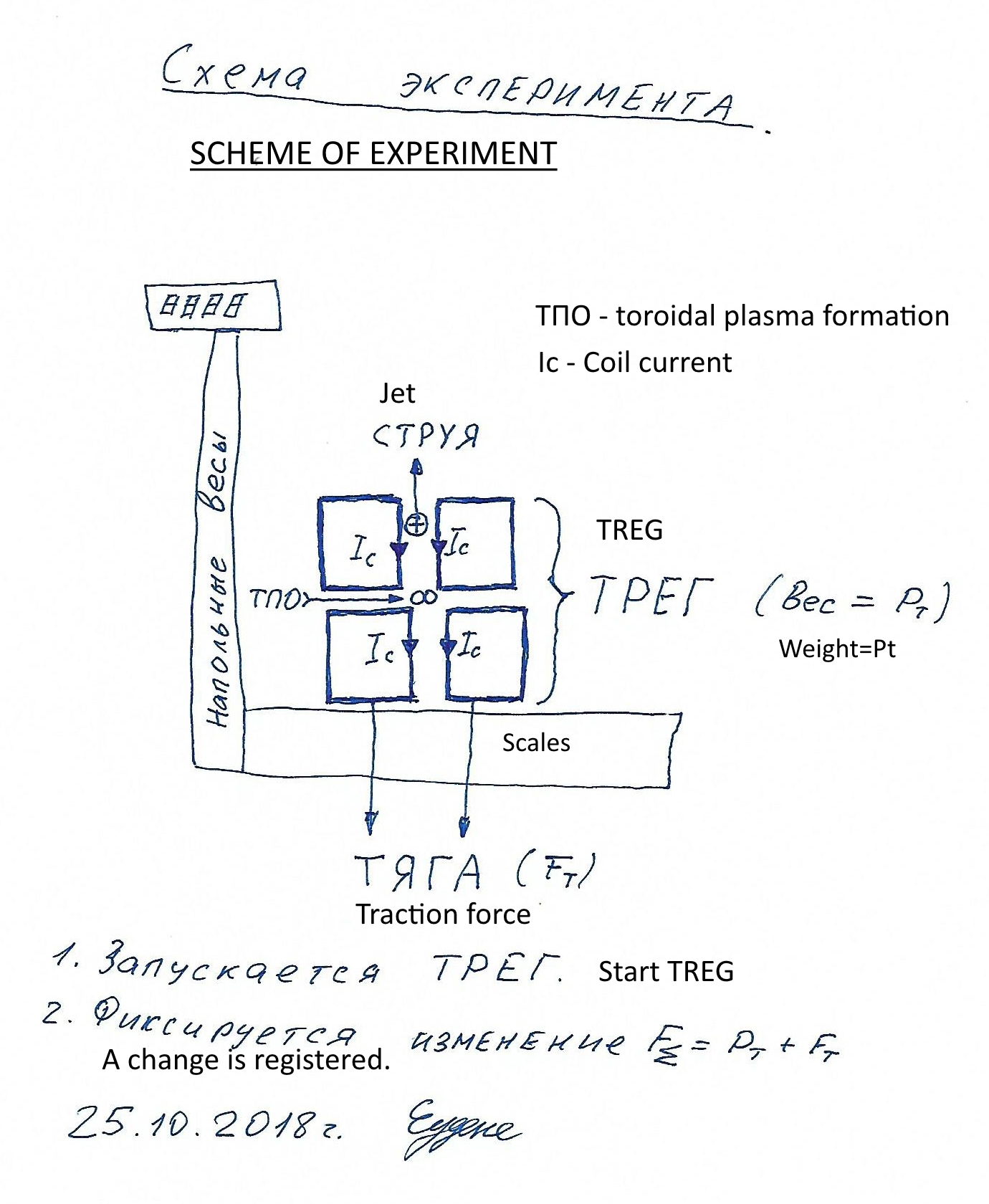
ж) Схема эксперимента.
Эксперимент должен быть поставлен именно в таком виде, чтобы сразу регистрировать и удержание плазмы и наличие реактивной тяги, так как шаровая молния (а именно её создание предполагается в эксперименте) может оказаться неустойчивой, взорваться и разрушить установку. Хотя пациент Стахович Андрей Николаевич (СПб, ул. Вёсельная), вместе с которым я "лежал" на Пряжке (отделение № 8), рассказывал, что однажды к нему в форточку залетела шаровая молния красного цвета, диаметром 2-3 мм, прожгла стенку стеклянного стакана и, оставив отверстие, исчезла без каких-либо эффектов. Катушки
(всего один комплект) могут быть предоставлены по запросу. Консультацию по направлению дальнейшей работы я могу предоставить дистанционно (e-mail: eugene-53@mail.ru, Skype: thermonuclear8) учёным всего мира.
ДО ПРОДЛЕНИЯ ЖИЗНИ И ПАНАЦЕИ ЧЕЛОВЕЧЕСТВО ЕЩЁ НЕ ДОРОСЛО - ПОЭТОМУ, Я ПРИДЕРЖУ ЭТО НОУ-ХАУ. На изготовленные по моему способу устройства обязательно приклеивать такое фото:
PER ASPERA AD ASTRA ЧЕРЕЗ ТЕРНИИ – К ЗВЁЗДАМ
Заключение.
Как видно из вышеприведённого, без натурных экспериментов это всё с большой, правда, степенью вероятности, но только предположения, всё требует экспериментальной проверки по всем указанным направлениям – всё, кроме экспериментально (!!!) установленного наличия ВНЕШНЕГО магнитного поля тороидальных проводящих структур с полоидальным электрическим током со специфической конфигурацией. Эксперименты в рамках психостационара проведены быть не могут – нет необходимой экспериментальной базы – созданного мною спецоборудования. Касаясь Разума и невежества можно сказать, что вера в сверхъестественные силы это никакая не опора в жизни – опорой могут служить только твёрдые знания и навыки, полученные на их основе в процессе обучения. Я дал Человечеству яд в виде оружия (средства скоростной доставки, космические системы, мощные лазеры, резеры, газеры, возможно гразеры, если гравитационные волны подчиняются законам волновой оптики), но дал и противоядие – установление в качестве всемирного законодательного базиса права Разума на существование и вселенского развития, а также выживание Человечества, как Вселенского вида существ, восприимчивых к Разуму. Борьба с невежеством во всех его формах, в том числе и в первую очередь со своим собственным, является обязанностью всех разумных людей.
Приложение 1 © Евгений Александрович Григорьев с помощью программы MathCad Январь 1997 года Впервые в науке - расчет магнитного поля внутри системы проводников, эквивалентной по электромагнитным свойствам полому замкнутому проводнику. Рассчитывается напряженность магнитного поля вдоль координатной оси X. Поверхностный ток Is, текущий по полому замкнутому проводнику между его полюсами А и В, можно представить в виде "нитей тока" i [И.Е. Тамм, Основы теории электричества, стр. 140], токов, текущих по математическим меридианам сферы от B к А.
Закон Био-Савара-Лапласа в векторной форме
Видно, что в пределах точности машинного счёта, МП внутри ПЗП равно нулю.
Приложение 2 Программа расчёта интенсивности магнитного поля внутри сферического полого замкнутого проводника вдоль координаты Х на языке программирования Quick BASIC 1995 год
'SFERA SCREEN 12 TIMER ON LOCATE 12, 1 COLOR 15 PRINT "Calculation of a magnetostatic field inside a Spherical Conductors System, which"; LOCATE 14, 2 PRINT "is equivalent by electromagnetic properties to a Closed and Hollow Conductor." ON TIMER(7) GOSUB 1 DO WHILE INKEY$ = "": LOOP 1 CLS Nl = 150 'number of lines with current in Spherical Conductor System Nds = 50 'number of elements of current in line of SCS DIM SG(Nds + 1), CG(Nds + 1) C$ = " +###.##" Pi = 3.14159265359# I = 10 'SCS line current IL = I * Nl 'current of Linear Conductor Ndl = Nds 'number of elements of current in Linear Conductor Rs = 20 L = Rs 'length of Linear Conductor strength dl = L / Ndl dg = 2 * Pi / Nds ds = Rs * dg FOR j = 0 TO Nds - 1 SG(j) = SIN(j * dg + dg / 2) CG(j) = COS(j * dg + dg / 2) NEXT j
LINE (500, 10)-(500, 60), 9 LOCATE 3, 64 COLOR 9 PRINT "LC"
CIRCLE (500, 110), 50, 15 LINE (500, 110)-(550, 110), 8 LOCATE 7, 66 COLOR 8 PRINT "Rs"
COLOR 5 LINE (20, 40)-(320, 40) 'X-axis LINE (20, 105)-(320, 105) 'Y-axis LINE (20, 165)-(320, 165) 'Z-axis LINE (20, 230)-(320, 230) 'SCS module-axis LINE (20, 300)-(320, 300) 'Linear current module-axis LINE (320, 10)-(320, 350), 8,, &HFF00 LOCATE 23, 40 COLOR 8 PRINT "Rs (radius of SCS," LOCATE 24, 30 PRINT "along which calculates a magnetic field)" FOR X = 0 TO Rs - 1 STEP 1 HVx = 0 HVy = 0 HVz = 0 Hs = 0 HCx = 0 HCy = 0 HCz = 0 HL = 0 FOR v = 0 TO Nds - 1 HUx = 0 HUy = 0 HUz = 0 FOR u = 0 TO Nl - 1 Rx = X - Rs * SG(v) * COS(u) Ry = -Rs * SG(v) * SIN(u) Rz = -Rs * CG(v) R3 = (SQR(Rx * Rx + Ry * Ry + Rz * Rz)) ^ 3 dsx = -ds * CG(v) * COS(u) dsy = -ds * CG(v) * SIN(u) dsz = ds * SG(v) Hsx = (dsy * Rz - Ry * dsz) / R3 Hsy = (dsz * Rx - Rz * dsx) / R3 Hsz = (dsx * Ry - Rx * dsy) / R3 HUx = HUx + Hsx HUy = HUy + Hsy HUz = HUz + Hsz NEXT u HVx = HVx + HUx HVy = HVy + HUy HVz = HVz + HUz Hs = SQR(HVx ^ 2 + HVy ^ 2 + HVz ^ 2)
RLx = X 'RLy = 0 RLz = Rs + dl * v + dl / 2
RL3 = (SQR(RLx * RLx + RLz * RLz)) ^ 3 'dlx = 0 'dly = 0 dlz = dl 'Hlx = (dly * RLz - RLy * dlz) / RL3 Hly = (dlz * RLx - RLz * dlx) / RL3 'Hlz = (dlx * RLy - RLx * dly) / RL3 'HCx = HCx + Hlx HCy = HCy + Hly 'HCz = HCz + Hlz
'HL = SQR(HCx ^ 2 + HCy ^ 2 + HCz ^ 2) HL = HCy NEXT v LOCATE 2, 1 COLOR 14 PRINT "Hsx ="; USING C$; I * HVx PSET (X * 300 / Rs + 20, HVx + 40)
COLOR 10 LOCATE 6, 1 PRINT "Hsy ="; USING C$; I * HVy PSET (X * 300 / Rs + 20, HVy + 105)
COLOR 11 LOCATE 10, 1 PRINT "Hsz ="; USING C$; I * HVz PSET (X * 300 / Rs + 20, HVz + 165)
COLOR 15 LOCATE 14, 1 PRINT "Hs ="; USING C$; I * Hs PSET (X * 300 / Rs + 20, Hs + 230) LOCATE 14, 25 PRINT "Magnetic intensity in Spherical Conductors System (SCS)" 'LOCATE 14, 25 'PRINT "in Spherical Conductors System (SCS)"
COLOR 9 LOCATE 18, 1 PRINT "HL ="; USING C$; HL * IL * 10 PSET (X * 300 / Rs + 20, HL * IL * 10 + 300) LOCATE 18, 25 PRINT "Magnetic intensity from Linear Conductor current (LC)"
NEXT X
FOR X = Rs TO Rs * 2 STEP 1 HCx = 0 HCy = 0 HCz = 0 HL = 0 FOR v = 0 TO Nds - 1 RLx = X 'RLy = 0 RLz = Rs + dl * v + dl / 2 RL3 = (SQR(RLx * RLx + RLz * RLz)) ^ 3 'dlx = 0 'dly = 0 dlz = dl 'Hlx = (dly * RLz - RLy * dlz) / RL3 Hly = (dlz * RLx - RLz * dlx) / RL3 'Hlz = (dlx * RLy - RLx * dly) / RL3 'HCx = HCx + Hlx HCy = HCy + Hly 'HCz = HCz + Hlz
'HL = SQR(HCx ^ 2 + HCy ^ 2 + HCz ^ 2) HL = HCy NEXT v PSET (X * 300 / Rs + 20, HL * IL * 10 + 300) NEXT X STOP COLOR 15 END
Приложение 3 Движение одной заряженной частицы в магнитном поле, создаваемом двумя другими движущимися частицами и между ними.
SCREEN 12 TIMER ON COLOR 3 LOCATE 2, 12 PRINT " Motion of one charged corpuscle (OMC)" LOCATE 4, 12 PRINT " in a magnetic field (MF) such as a Magnetic; Cocoon," LOCATE 6, 12 PRINT "which is created by two others mobile charged corpuscles (TMC)" LOCATE 8, 25 PRINT "Etmc = 5 eV; Eomc = 50 eV" ON TIMER(5) GOSUB 1 DO WHILE INKEY$ = "": LOOP
1 CLS C$ = " +#.#####^^^^" Pi = 3.141593 Mo = 4 * Pi *.0000001 K = Mo / (4 * Pi) 'SI M = 1.67E-27 * 2 '[kg] Q = 1.6E-19 '[C]
LOCATE 6, 2 COLOR 9 INPUT "distance between TMC [sm](10 - 50)="; A0 a = A0 *.01 '[m] distance between TMC Xk1 = 0 Yk1 = 0 Xk2 = Xk1 + a Yk2 = 0 CIRCLE (Xk1 * 1000 + 50, Yk1 + 240), 10, 9 CIRCLE (Xk2 * 1000 + 50, Yk2 + 240), 10, 9 Ek = 5 '[eV] energy of TMC TVk = 0 'angle of moving of TMC Vk = SQR(2 * Ek * ABS(Q) / M) 'velocity of TMC Vkx = Vk * COS(TVk) Vky = 0 Vkz = 0 LOCATE 1, 60 PRINT "V tmc ="; USING C$; Vk
COLOR 13 Eq = 50 '[eV] energy of entry of OMC LOCATE 8, 2 INPUT "angle of entry of OMC (0 - 360)="; TVq Vq = SQR(2 * Eq * ABS(Q) / M) 'velocity of OMC Vqx = Vq * COS(TVq) Vqy = Vq * SIN(TVq) Vqz = 0 LOCATE 3, 60 PRINT "V omc ="; USING C$; Vq dlq =.0001# 'step of moving of OMC Xq = Xk1 +.5 * a 'coordinate began movements of OMC LOCATE 10, 2 INPUT "Coordinate Y began movements of OMC [sm](-25/+25)="; Yq0 COLOR 8
Yq = Yq0 *.01 Zq = 0
Fx = 0 Fy = 0 Fz = 0 FOR t = 0 TO 100000 dt = dlq / Vq Rx1 = Xq - Xk1 Rx2 = Xq - Xk2
Ry1 = Yq - Yk1 Ry2 = Yq - Yk2 'Rz1 = 0 Rz2 = 0
R1 = SQR(Rx1 * Rx1 + Ry1 * Ry1) R2 = SQR(Rx2 * Rx2 + Ry2 * Ry2)
'B = K * Q * [V x R] / R^3 MF, created by TMC [Tl] 'Bx1 = K * Q * (Vky * Rz1 - Ry1 * Vkz) / R1 ^ 3 == 0 'By1 = K * Q * (Vkz * Rx1 - Rz1 * Vkx) / R1 ^ 3 == 0 Bz1 = K * Q * (Vkx * Ry1 - Rx1 * Vky) / R1 ^ 3
'Љ—2 'Bx2 = K * Q * (Vky * Rz2 - Ry2 * Vkz) / R2 ^ 3 == 0 'By2 = K * Q * (Vkz * Rx2 - Rz2 * Vkx) / R2 ^ 3 == 0 Bz2 = K * Q * (Vkx * Ry2 - Rx2 * Vky) / R2 ^ 3
'Lorentz force which influence on OMC FL = Q*[V x B] 'Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz) 'Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx) 'Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
Fx = Vqy * (Bz1 + Bz2) Fy = -(Bz1 + Bz2) * Vqx 'Fz = (Vqx * (By1 + By2) - (Bx1 + Bx2) * Vqy) ==0
'F = M*dV/dt = FL = Q*[V x Bk] ==> dV=PX*dt/M
dVqx = Fx * dt / M dVqy = Fy * dt / M dVqz = 0 'dVz = Fz * dt / M Vqxt = Vqx + dVqx Vqyt = Vqy + dVqy Vqzt = 0 'Vqzt = Vqz + dVqz Vqt = SQR(Vqxt ^ 2 + Vqyt ^ 2) '+ Vqzt ^ 2) kV = Vq / Vqt 'kV - because velocity of OMC must be constant Vqx = Vqxt * kV Vqy = Vqyt * kV Vqz = 0 'Vqz = Vqzt * kV V = SQR(Vqx ^ 2 + Vqy ^ 2) '+ Vqz ^ 2) dXq = Vqx * dt dYq = Vqy * dt dZq = 0 'dZq = Vz * dt Xq = Xq + dXq Yq = Yq + dYq Zq = 0 'Zq = Zq + dZq PSET (Xq * 1000 + 50, Yq * 1000 + 240), 13 NEXT t END
Приложение 4 Движение заряженной частицы в магнитном поле типа «Магнитный кокон».
SCREEN 12 TIMER ON COLOR 3 LOCATE 3, 17 PRINT " Motion of one deuteron in a magnetic field " LOCATE 5, 17 PRINT " such as a Magnetic Cocoon " LOCATE 7, 17 PRINT " Ed = 500 eV" COLOR 15 ON TIMER(3) Gosub 1 DO While INKEY$ = "": LOOP
1 CLS Dim X1(80), X2(80) C$ = " +#.#####^^^^" Pi = 3.141593 Mo = 4 * Pi *.0000001 M = 1.67E-27 * 2 Q = 1.6E-19 E = 500 '[eV] 2 CLS LOCATE 2, 10 INPUT "ANGLE (50 - 175)="; AN If 175 < AN Goto 2 If AN < 50 Goto 2 TV = AN * Pi / 180 V = Sqr(2 * E * Abs(Q) / M) Vx = V * Cos(TV) Vy = V * Sin(TV) Vz = 0 LOCATE 2, 60 PRINT "V ="; USING C$; V dlq =.0002 'dt = dlq / V A =.04 YL1 = 0 YL2 = 0 Xv = 0 Yv =.001 Zv = 0 L =.08 DL =.001 N = L / DL IL = 3000000 K = Mo / (4 * Pi) For I = 0 To N - 1 X1(I) = -I * DL - DL / 2 - A X2(I) = I * DL + DL / 2 + A Next I For t = 0 To 3000 dt = dlq / V PXx = 0 PXy = 0 PXz = 0 For I = 0 To N - 1 Rx1 = Xv - X1(I) Rx2 = Xv - X2(I) Ux = DL Uy = 0 Uz = 0 Ry1 = Yv + YL1 Ry2 = Yv + YL2 Rz = Zv R1 = Sqr(Rx1 * Rx1 + Ry1 * Ry1 + Rz * Rz) R2 = Sqr(Rx2 * Rx2 + Ry2 * Ry2 + Rz * Rz)
Hy1 = (-Rz * Ux) / R1 ^ 3 Hz1 = (Ux * Ry1) / R1 ^ 3
Hy2 = (-Rz * Ux) / R2 ^ 3 Hz2 = (Ux * Ry2) / R2 ^ 3 Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz) Py = -(Hz1 + Hz2) * Vx Pz = Vx * (Hy1 + Hy2) PXx = PXx + Px PXy = PXy + Py PXz = PXz + Pz Next I dVx = Q * K * IL * PXx * dt / M dVy = Q * K * IL * PXy * dt / M dVz = Q * K * IL * PXz * dt / M Vxt = Vx + dVx Vyt = Vy + dVy Vzt = Vz + dVz Vt = Sqr(Vxt ^ 2 + Vyt ^ 2 + Vzt ^ 2) kV = V / Vt 'kV - the particle must have a constant value modulo of velocity Vx = Vxt * kV Vy = Vyt * kV Vz = Vzt * kV V = Sqr(Vx ^ 2 + Vy ^ 2 + Vz ^ 2) dXv = Vx * dt dYv = Vy * dt dZv = Vz * dt Xv = Xv + dXv Yv = Yv + dYv Zv = Zv + dZv PSET (Xv * 10000 + 320, Yv * 10000 + 240), 12 Next t End
Приложение 5 Движение двух заряженных частиц в магнитном поле типа «Магнитный кокон» с учётом Кулоновского взаимодействия.
SCREEN 12 TIMER ON COLOR 3 LOCATE 3, 17 PRINT " Motion of two deuterones in a magnetic field " LOCATE 5, 17 PRINT " such as a Magnetic Cocoon " COLOR 15 ON TIMER(3) GOSUB 1 DO WHILE INKEY$ = "": LOOP
1
CLS DIM XP1(150), XP2(150) C$ = " #.###^^^^" Pi = 3.141593 Eo = 8.85E-12 Mo = 4 * Pi *.0000001 M = 1.67E-27 * 2 Q = 1.6E-19 E = 700! '[eV] J = 8E+08 LOCATE 3, 10 INPUT "ANGLE (30 - 170)="; AN IF 170 < AN GOTO 1 IF AN < 30 GOTO 1 TV = AN * Pi / 180 V = SQR(2 * E * ABS(Q) / M) Vx1 = V * COS(TV) Vy1 = V * SIN(TV) Vz1 = 0 Vx2 = Vx1 Vy2 = -Vy1 dlq =.0001 A =.007 Xv1 = 0 Yv1 =.0003 Xv2 = 0 Yv2 = -.0003 L =.25 DL =.01 N = L / DL Du =.06 S = Pi * Du ^ 2 / 4 IL = S * J K = Mo / (4 * Pi) FOR I = 0 TO N - 1 XP1(I) = -I * DL - DL / 2 - A XP2(I) = I * DL + DL / 2 + A NEXT I FOR t = 0 TO 8000 IL = S * J K1 = 5000000! dt = dlq / V LOCATE 2, 65 PRINT "t ="; USING C$; t * dt PXx1 = 0 PXy1 = 0 PXx2 = 0 PXy2 = 0 PCx1 = 0 PCy1 = 0 PCx2 = 0 PCy2 = 0 FOR I = 0 TO N - 1 Rx11 = Xv1 - XP1(I) Rx12 = Xv1 - XP2(I) Rx21 = Xv2 - XP1(I) Rx22 = Xv2 - XP2(I) Ux = DL REM Uy = 0 Uz = 0 Ry1 = Yv1 Ry2 = Yv2
R11 = SQR(Rx11 * Rx11 + Ry1 * Ry1) R12 = SQR(Rx12 * Rx12 + Ry1 * Ry1) R21 = SQR(Rx21 * Rx21 + Ry2 * Ry2) R22 = SQR(Rx22 * Rx22 + Ry2 * Ry2) RGx1 = Xv1 - Xv2 RGy1 = Yv1 - Yv2 RG1 = SQR(RGx1 ^ 2 + RGy1 ^ 2) RGx2 = -RGx1 RGy2 = -RGy1 RG2 = RG1
REM Hx1 = (Uy * Rz - Ry * Uz) / R1 ^ 3 REM Hy1 = (Uz * Rx1 - Rz * Ux) / R1 ^ 3 REM Hz1 = (Ux * Ry - Rx1 * Uy) / R1 ^ 3
Hz11 = (Ux * Ry1) / R11 ^ 3 Hz12 = (Ux * Ry1) / R12 ^ 3 Hz21 = (Ux * Ry2) / R21 ^ 3 Hz22 = (Ux * Ry2) / R22 ^ 3
REM Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz) REM Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx) REM Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
PGx1 = RGx1 / (ABS(RG1 ^ 3)) * K1 PGy1 = RGy1 / (ABS(RG1 ^ 3)) * K1 PGx2 = RGx2 / (ABS(RG2 ^ 3)) * K1 PGy2 = RGy2 / (ABS(RG2 ^ 3)) * K1 'Coefficient "K1" imitates group of particles Px1 = Vy1 * (Hz11 + Hz12) Py1 = -(Hz11 + Hz12) * Vx1 Px2 = Vy2 * (Hz21 + Hz22) Py2 = -(Hz21 + Hz22) * Vx2
PCx1 = PCx1 + PGx1 PCy1 = PCy1 + PGy1 PCx2 = PCx2 + PGx2 PCy2 = PCy2 + PGy2
PXx1 = PXx1 + Px1 PXy1 = PXy1 + Py1 PXx2 = PXx2 + Px2 PXy2 = PXy2 + Py2
NEXT I dVx1 = Q * K * IL * PXx1 * dt / M dVy1 = Q * K * IL * PXy1 * dt / M dVx2 = Q * K * IL * PXx2 * dt / M dVy2 = Q * K * IL * PXy2 * dt / M
Vxt1 = Vx1 + dVx1 Vyt1 = Vy1 + dVy1 Vt1 = SQR(Vxt1 ^ 2 + Vyt1 ^ 2) kV1 = V / Vt1
Vxt2 = Vx2 + dVx2 Vyt2 = Vy2 + dVy2 Vt2 = SQR(Vxt2 ^ 2 + Vyt2 ^ 2) kV2 = V / Vt2 'kV - the particle must have a constant value modulo of velocity dVCx1 = Q ^ 2 * PCx1 * dt / M / (4 * Pi * Eo) dVCy1 = Q ^ 2 * PCy1 * dt / M / (4 * Pi * Eo) dVCx2 = Q ^ 2 * PCx2 * dt / M / (4 * Pi * Eo) dVCy2 = Q ^ 2 * PCy2 * dt / M / (4 * Pi * Eo)
Vx1 = Vxt1 * kV1 + dVCx1 Vy1 = Vyt1 * kV1 + dVCy1 Vx2 = Vxt2 * kV2 + dVCx2 Vy2 = Vyt2 * kV2 + dVCy2 Vt = SQR(Vx1 ^ 2 + Vy1 ^ 2 + Vz1 ^ 2)
REM LOCATE 23, 20 REM PRINT "Vt ="; USING C$; Vt
dXv1 = Vx1 * dt dYv1 = Vy1 * dt dXv2 = Vx2 * dt dYv2 = Vy2 * dt
Xv1 = Xv1 + dXv1 Yv1 = Yv1 + dYv1 Xv2 = Xv2 + dXv2 Yv2 = Yv2 + dYv2
PSET (Xv1 * 70000 + 320, Yv1 * 60000 + 240), 9 PSET (Xv2 * 70000 + 320, Yv2 * 60000 + 240), 12
IF t = 2000 THEN CLS 1 IF t = 5000 THEN CLS 1 IF t = 6500 THEN CLS 1 NEXT t LOCATE 29, 5 INPUT "repeat under other angle - 1 "; U1 IF U1 = 1 THEN GOTO 1 IF U1 <> 1 THEN END
Приложение 6 Движение двух заряженных частиц в нарастающем магнитном поле типа «Магнитный кокон» - «Сферический пинч».
SCREEN 12 TIMER ON COLOR 3 LOCATE 3, 12 PRINT " Motion of two deuterones" LOCATE 5, 12 PRINT " in a increasing magnetic field such as a Magnetic Cocoon " LOCATE 7, 12 PRINT " (Spherical pinch)" COLOR 15 ON TIMER(4) GOSUB 1 DO WHILE INKEY$ = "": LOOP
1 CLS DIM XP1(80), XP2(80) C$ = " ##.###^^^^" Pi = 3.141593 Eo = 8.85E-12 Mo = 4 * Pi *.0000001 M = 1.67E-27 * 2 Q = 1.6E-19 E = 10000 '[eV] J = 7E+10 LOCATE 2, 10 INPUT "ANGLE (60 - 300)="; AN IF 300 < AN GOTO 1 IF AN < 60 GOTO 1 TV = AN * Pi / 180 V = SQR(2 * E * ABS(Q) / M) Vx1 = V * COS(TV) Vy1 = V * SIN(TV) Vz1 = 0 Vx2 = Vx1 Vy2 = -Vy1 dlq =.0003 A =.015 Xv1 = 0 Yv1 =.001 Xv2 = 0 Yv2 = -.001 L =.08 DL =.001 N = L / DL Du =.01 s = Pi * Du ^ 2 / 4 IL = s * J K = Mo / (4 * Pi) FOR i = 0 TO N - 1 XP1(i) = -i * DL - DL / 2 - A XP2(i) = i * DL + DL / 2 + A 'PSET ((XP1(I) * 2000 + 320 - A * 5000), 240) 'PSET ((XP2(I) * 2000 + 320 + A * 5000), 240) NEXT i tt = 0 FOR t = 0 TO 8000 dt = dlq / V tt = tt + dt LOCATE 2, 65 PRINT "t ="; USING C$; tt LOCATE 4, 65 PRINT "I ="; USING C$; IL
PXx1 = 0 PXy1 = 0 PXx2 = 0 PXy2 = 0 PCx1 = 0 PCy1 = 0 PCx2 = 0 PCy2 = 0 FOR i = 0 TO N - 1 Rx11 = Xv1 - XP1(i) Rx12 = Xv1 - XP2(i) Rx21 = Xv2 - XP1(i) Rx22 = Xv2 - XP2(i) Ux = DL REM Uy = 0 Uz = 0 Ry1 = Yv1 Ry2 = Yv2
R11 = SQR(Rx11 * Rx11 + Ry1 * Ry1) R12 = SQR(Rx12 * Rx12 + Ry1 * Ry1) R21 = SQR(Rx21 * Rx21 + Ry2 * Ry2) R22 = SQR(Rx22 * Rx22 + Ry2 * Ry2) RGx1 = Xv1 - Xv2 RGy1 = Yv1 - Yv2 RG1 = SQR(RGx1 ^ 2 + RGy1 ^ 2) RGx2 = -RGx1 RGy2 = -RGy1 RG2 = RG1
REM Hx1 = (Uy * Rz - Ry * Uz) / R1 ^ 3 REM Hy1 = (Uz * Rx1 - Rz * Ux) / R1 ^ 3 REM Hz1 = (Ux * Ry - Rx1 * Uy) / R1 ^ 3
Hz11 = (Ux * Ry1) / R11 ^ 3 Hz12 = (Ux * Ry1) / R12 ^ 3 Hz21 = (Ux * Ry2) / R21 ^ 3 Hz22 = (Ux * Ry2) / R22 ^ 3
REM Px = (Vy * (Hz1 + Hz2) - (Hy1 + Hy2) * Vz) REM Py = (Vz * (Hx1 + Hx2) - (Hz1 + Hz2) * Vx) REM Pz = (Vx * (Hy1 + Hy2) - (Hx1 + Hx2) * Vy)
PGx1 = RGx1 / (ABS(RG1 ^ 3)) PGy1 = RGy1 / (ABS(RG1 ^ 3)) PGx2 = RGx2 / (ABS(RG2 ^ 3)) PGy2 = RGy2 / (ABS(RG2 ^ 3))
Px1 = Vy1 * (Hz11 + Hz12) Py1 = -(Hz11 + Hz12) * Vx1 Px2 = Vy2 * (Hz21 + Hz22) Py2 = -(Hz21 + Hz22) * Vx2
PCx1 = PCx1 + PGx1 PCy1 = PCy1 + PGy1 PCx2 = PCx2 + PGx2 PCy2 = PCy2 + PGy2
PXx1 = PXx1 + Px1 PXy1 = PXy1 + Py1 PXx2 = PXx2 + Px2 PXy2 = PXy2 + Py2
NEXT i dVx1 = Q * K * IL * PXx1 * dt / M dVy1 = Q * K * IL * PXy1 * dt / M dVx2 = Q * K * IL * PXx2 * dt / M dVy2 = Q * K * IL * PXy2 * dt / M
Vxt1 = Vx1 + dVx1 Vyt1 = Vy1 + dVy1 Vt1 = SQR(Vxt1 ^ 2 + Vyt1 ^ 2) kV1 = V / Vt1
Vxt2 = Vx2 + dVx2 Vyt2 = Vy2 + dVy2 Vt2 = SQR(Vxt2 ^ 2 + Vyt2 ^ 2) kV2 = V / Vt2
'kV - the particle must have a constant value modulo of velocity
kq = 3000 'Magnification of distance of a Coulomb interaction 'imitates group of particles
dVCx1 = (kq * Q) ^ 2 * PCx1 * dt / M / (4 * Pi * Eo) dVCy1 = (kq * Q) ^ 2 * PCy1 * dt / M / (4 * Pi * Eo) dVCx2 = (kq * Q) ^ 2 * PCx2 * dt / M / (4 * Pi * Eo) dVCy2 = (kq * Q) ^ 2 * PCy2 * dt / M / (4 * Pi * Eo)
Vx1 = Vxt1 * kV1 + dVCx1 Vy1 = Vyt1 * kV1 + dVCy1 Vx2 = Vxt2 * kV2 + dVCx2 Vy2 = Vyt2 * kV2 + dVCy2 Vt = SQR(Vx1 ^ 2 + Vy1 ^ 2 + Vz1 ^ 2)
REM LOCATE 23, 20 REM PRINT "Vt ="; USING C$; Vt
dXv1 = Vx1 * dt dYv1 = Vy1 * dt dXv2 = Vx2 * dt dYv2 = Vy2 * dt
Xv1 = Xv1 + dXv1 Yv1 = Yv1 + dYv1 Xv2 = Xv2 + dXv2 Yv2 = Yv2 + dYv2
PSET (Xv1 * 25000 + 320, Yv1 * 25000 + 240), 9 PSET (Xv2 * 25000 + 320, Yv2 * 25000 + 240), 4
Y12 = Yv1 - Yv2 IF Y12 <.0000000000002# THEN dlq =.00000000000001# IF Y12 >.0000000000002# THEN dlq =.00000000000002# IF Y12 >.000000000002# THEN dlq =.0000000000002# IF Y12 >.00000000002# THEN dlq =.000000000002# IF Y12 >.0000000002# THEN dlq =.00000000002# IF Y12 >.000000002# THEN dlq =.0000000002# IF Y12 >.00000002# THEN dlq =.000000002# IF Y12 >.0000002# THEN dlq =.00000002# IF Y12 >.000002 THEN dlq =.0000002# IF Y12 >.00002 THEN dlq =.000004# IF Y12 >.0002 THEN dlq =.00004# IF Y12 >.002 THEN dlq =.0001#
IF t = 7000 THEN CLS 1
J = J + 8E+07 IL = s * J NEXT t
LOCATE 29, 5 INPUT "Repeat with other angle - 1 "; U1 IF U1 = 1 THEN GOTO 1 IF U1 <> 1 THEN END
Приложение 7 Движение электрона в магнитном поле тора с полоидальным током – «Ондулятор».
SCREEN 12 COLOR 3 LOCATE 5, 5 PRINT " Motion of an electron in a magnetic field " LOCATE 7, 5 PRINT " such as a Magnetic Cocoon (undulator) " COLOR 15 C$ = " +#.#####^^^^" Pi = 3.14159265359# M = 9.1E-31 Q = 1.6E-19 jc = 6E+08 dt = 3E-10 Uq = 400! Du =.001 TV = 30 * Pi / 180 K = 4 * Pi *.0000001 * (-Q) * (jc * Du ^ 2 / 4) / (4 * Pi) V = SQR(2 * Q * Uq / M) Vx = V * COS(TV) Vy = V * SIN(TV) Vz = 0 LOCATE 3, 60 PRINT "V= "; USING C$; V A =.03 X1 = -.05 X2 =.05 dX = (X2 - X1) / 100 dG = Pi / 50 Xv = -.32 Yv = 0 Zv = 0 PSET (Xv * 1200 + 420, Yv * 4000 + 300) DIM X(100) FOR i = 0 TO 99 X(i) = X1 + i * dX + dX / 2 PSET (X(i) * 1200 + 420, A * 4000 + 300) PSET (X(i) * 1200 + 420, -A * 4000 + 300) NEXT i PGx = 0 PGy = 0 PGz = 0 FOR t = 1 TO 100 FOR j = 0 TO 99 CG = COS(j * dG) SG = SIN(j * dG) PXx = 0 PXy = 0 PXz = 0 Ry = -A * CG + Yv Rz = -A * SG + Zv Ry2 = Ry * Ry Rz2 = Rz * Rz Ux = dX 'Uy = 0 Uz = 0 FOR i = 0 TO 99 Rx = -X(i) + Xv 'R = SQR(Rx * Rx + Ry2 + Rz2) R3 = (SQR(Rx * Rx + Ry2 + Rz2)) ^ 3 Hx = (Vy * Rz - Vz * Ry) / R3 Hy = (Vz * Rx - Vx * Rz) / R3 Hz = (Vx * Ry - Vy * Rx) / R3 'Px = Uy * Hz - Uz * Hy Py = -Ux * Hz 'Py = Uz * Hx - Ux * Hz Pz = Ux * Hy 'Pz = Ux * Hy - Uy * Hx 'PXx = PXx + Px PXy = PXy - Py PXz = PXz - Pz NEXT i 'PGx = PGx + PXx PGy = PGy + PXy PGz = PGz + PXz NEXT j 'dVx = K * PGx * dt / M dVy = K * PGy * dt / M dVz = K * PGz * dt / M Vxt = Vx + dVx Vyt = Vy + dVy Vzt = Vz + dVz Vt = SQR(Vxt ^ 2 + Vyt ^ 2 + Vzt ^ 2) kV = V / Vt 'kV - the particle must have a constant value modulo of velocity Vx = Vxt * kV Vy = Vyt * kV Vz = Vzt * kV V = SQR(Vx ^ 2 + Vy ^ 2 + Vz ^ 2) dXv = Vx * dt dYv = Vy * dt dZv = Vz * dt Xv = Xv + dXv Yv = Yv + dYv Zv = Zv + dZv PSET (Xv * 1200 + 420, Yv * 4000 + 300), 12 NEXT t
Приложение 8 © Григорьев Евгений Александрович. 2004 год.
|
|||||||||
|
Последнее изменение этой страницы: 2021-04-20; просмотров: 102; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.137.162 (0.015 с.) |






 Это значительно упрощает программу расчета магнитного поля внутри системы проводников, эквивалентной по электромагнитным свойствам (в необходимом приближении) сферическому полому замкнутому проводнику (ПЗП).
Это значительно упрощает программу расчета магнитного поля внутри системы проводников, эквивалентной по электромагнитным свойствам (в необходимом приближении) сферическому полому замкнутому проводнику (ПЗП).




















