Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления	Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ Написать работу Область допустимых решений задачи линейного программирования имеет вид, изображенный на рисунке. Может ли быть получено оптимальное решение в точке М. ↑ ▷ Содержание ⇐ ПредыдущаяСтр 7 из 7 Содержание книги Тест по разделу 1 (элементы теории принятия решений) Верно ли утверждение: «принятие решения не является этапом процесса управления» . За кем остается последнее слово при принятии решений. Символически задача принятия решения типа J – это Тест по разделу 2 (разработка и принятие оптимальных решений в задачах с линейными функциями) Для решения следующей транспортной задачи Область допустимых решений задачи линейного программирования имеет вид, изображенный на рисунке. Может ли быть получено оптимальное решение в точке М. Поиск на нашем сайте М Х1 Х2 1) да 2) нет 3) однозначного ответа нет     ОДР   Область допустимых решений задачи линейного программирования имеет вид, изображенный на рисунке. Может ли быть получено оптимальное решение в точке М? ОДР Х1 Х2 1) да 2) нет 3) однозначного ответа нет М       34. Область допустимых решений задачи линейного программирования имеет вид, изображенный на рисунке. Может ли быть получено оптимальное решение одновременно в точках М1 и М2? ОДР Х1 Х2 1) да 2) нет 3) однозначного ответа нет М1      М2     35. В результате решения задачи максимизации прибыли предприятия после некоторого шага получена таблица 1. Таблица 1 i Базис	сб	P0	-2	1	0	1	0	0	-М	-М
P1	P2			P3	P4	P5	P6	Р7	Р8
1	P3	0	10	1	-2	1	0	0	0	0	0
2	P7	-М	18	-2	-1	0	-2	-1	0	1	0
3	P8	-М	36	3	2	0	1	0	-1	0	1
4
5

 

 Задача решается методом:

1) графическим;

2) симплекс – методом

3) методом искусственного базиса

4) методом потенциалов

 

 

36. В результате решения задачи максимизации прибыли предприятия после первого шага метода симплекс – таблиц получена таблица 1.

Таблица 1.

i	Базис	сб	P 0	9	10	16	0	0	0
				P 1	P 2	P 3	P 4	P 5	P 6
1	P4	0	360	18	15	12	1	0	0
2	P5	0	192	6	4	8	0	1	0
3	P6	0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Является ли этот план допустимым?

1) Да

2) нет

3) однозначного ответа нет

 

37. В результате решения задачи максимизации прибыли предприятия после первого шага метода симплекс – таблиц получена таблица 1.

Таблица 1.

i	Базис	сб	P 0	9	10	16	0	0	0
				P 1	P 2	P 3	P 4	P 5	P 6
1	P4	0	360	18	15	12	1	0	0
2	P5	0	192	6	4	8	0	1	0
3	P6	0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Является ли этот план оптимальным?

1) Да

2) нет

3) однозначного ответа нет

 

 38. В результате решения задачи максимизации прибыли предприятия после первого шага метода симплекс – таблиц получена таблица 1.

Таблица 1.

i	Базис	сб	P 0	9	10	16	0	0	0
				P 1	P 2	P 3	P 4	P 5	P 6
1	P4	0	360	18	15	12	1	0	0
2	P5	0	192	6	4	8	0	1	0
3	P6	0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Какой вектор должен быть введен в базис?

1) Р₁

2) Р₂

3) Р₃

39. В результате решения задачи максимизации прибыли предприятия после первого шага метода симплекс – таблиц получена таблица 1.

Таблица 1.

i	Базис	сб	P 0	9	10	16	0	0	0
				P 1	P 2	P 3	P 4	P 5	P 6
1	P4	0	360	18	15	12	1	0	0
2	P5	0	192	6	4	8	0	1	0
3	P6	0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Какой вектор должен быть выведен из базиса?

1) Р₁

2) Р₂

3) Р₃

40. В результате решения задачи максимизации прибыли предприятия после некоторого шага метода симплекс – таблиц получена таблица 1.

Таблица 1

i	Базис	сб	P0	2	-6	0	0	5	0
				P1	P2	P3	P4	P5	P6
1	P3	0	12	-5/3	5/3	1	-1/3	0	0
2	P5	5	8	-1/3	-2/3	0	1/3	1	0
3	P6	0	114	-1	- 9	0	4	0	1
4

 

 Значение элемента индексной строки вектора Р₂ должно быть:

 

1) 4

2) 1

3) 12

4) 6

5) 1/3

 

41. В транспортной задаче методом северо-западного угла необходимо назначить перевозку из пункта А₁ в пункт В₁

 

	В1	В2	В3	В4	Запас
А1	2	3	2	2	220
А2	3	4	5	6	340
А3	4	3	5	7	230
Потр.	120	160	210	300	790

 

1) 160

2) 210

3) 300

4) 120

5) 230

 

Матрица оценок свободных клеток после применения метода потенциалов к транспортной задаче имеет вид

 

                                          

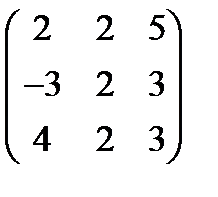
Является ли полученное решение оптимальным?

1) да

2) нет

3) однозначного ответа нет

Матрица оценок свободных клеток после применения метода потенциалов к транспортной задаче имеет вид

 

                                          

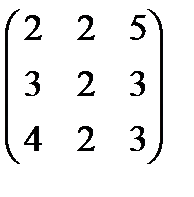
Является ли полученное решение оптимальным?

1) да

2) нет

3) однозначного ответа нет

 

Если в разрешающем столбце симплекс-таблицы при решении задачи линейного программирования на максимум в разрешающем столбце нет положительных коэффициентов, то это означает, что

1) получено оптимальное решение

2) целевая функция не ограничена сверху

3) область допустимых решений пуста

 

45. Чему равны небазисные переменные в оптимальном плане задачи линейного программирования?

1) нулю

2) любому положительному числу

3) любому числу

⇐ Предыдущая1234567

Поделиться: