
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция «Векторы. Векторная алгебра»Стр 1 из 3Следующая ⇒
АЛГЕБРА И ГЕОМЕТРИЯ КОНСПЕКТЫ ЛЕКЦИЙ ВЕКТОРЫ. ВЕКТОРНАЯ АЛГЕБРА
Действия над векторами В качестве действий над векторами, рассматриваются линейные операции – умножение вектора на число, сложение и вычитание. Умножение вектора на число Определение 6. Произведением вектора На рис. 6 – рис. 9 показаны пары векторы
Рис. 3. Случай
Рис. 4. Случай
Рис. 5. Случай
Рис. 6. Случай
Противоположный вектор
Отметим некоторые свойства умножения вектора на число.
1.
2.
3.
4. Теорема 1. Для коллинеарности векторов Сумма векторов Определение 7. Суммой векторов
Рис. 10
Отметим некоторые свойства суммы векторов.
1.
2.
3.
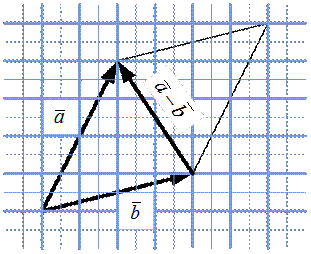
4. Разность векторов Определение 8. Разностью Разность Сумма и разность векторов определялись по правилу параллелограмма. Можно эти две операции определить по правилу треугольника. Для определения суммы
Рис. 11
Числовая ось Числовой осью (числовой прямой) называется любая прямая, если: 1) на ней выбрана некоторая точка, называемая началом (центром) и обозначаемая
2) любое из двух направлений, называемое положительным направлением и обозначаемое стрелкой;
3) некоторый отрезок, называемый единичным отрезком (масштабом).
Каждому вещественному числу на числовой прямой соответствует единственная точка на числовой оси: 1) положительное число 2) отрицательное число 3) нулевое число Имеет место и обратное соответствие: каждой точке на числовой оси соответствует единственное вещественное число. Пусть точке
Единичный вектор
Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором. Пусть задан вектор
Для каждой числовой оси
Рис. 12
Угол между векторами Определение 10. Пусть векторы Из определения вытекает, что угол Определение 11. Пусть начало вектора
Рис. 13 Рис. 14 Проекция вектора на ось Определение 12. Проекцией точки
Рис. 15 Определение 13. Проекцией вектора
Рис. 16
Проекция вектора
Обозначим через Проекция вектора может быть: 1) положительной, если угол
Рис. 17 Рис. 18
Определение 13. Составляющей вектора
Составляющей вектора
сост
Отметим некоторые свойства проекции вектора на ось. Свойство 1. Проекция вектора
Свойство 2. Проекция произведения вектора
Свойство 3. Проекция суммы двух векторов
Свойство 4. Проекция разности двух векторов
Системы координат Длина вектора Пусть
АЛГЕБРА И ГЕОМЕТРИЯ КОНСПЕКТЫ ЛЕКЦИЙ ВЕКТОРЫ. ВЕКТОРНАЯ АЛГЕБРА
Лекция «Векторы. Векторная алгебра»
Основные определения. Действия над векторами: умножение вектора на число; сумма векторов; разность векторов. Числовая ось. Единичный вектор. Угол между векторами. Проекция вектора на ось. Системы координат: декартова система координат на плоскости; декартова система координат в пространстве. Длина вектора. Расстояние между двумя точками. Направляющие косинусы вектора. Скалярное произведение двух векторов: определение скалярного произведения; свойства скалярного произведения. Векторное произведение двух векторов: определение векторного произведения; свойства векторного произведения. Смешанное произведение трёх векторов: определение смешанного произведения; свойства смешанного произведения
1. Основные определения В физике и технических науках встречаются величины, которые полностью определяются заданием их численных значений. Эти численные значения являются вещественными числами. Такие величины называются скалярными. Скалярными величинами являются длина, площадь, объём, масса, температура и др. Наряду со скалярными, встречаются величины, для определения которых необходимо знать их направления в пространстве, например, сила, скорость, ускорение и т.д. Такие величины называются векторными. Они описываются с помощью векторов. Определение 1. Вектором (свободным вектором) О всяком отрезке из этого множества говорят, что он представляет вектор. Одна из ограничивающих его точек принимается за начало, другая – за конец, который на рисунке показывается стрелкой. Если началом вектора является точка
Рис. 1 Рис. 2
Определение 2. Модулем вектора Определение 3. Вектор, у которого конец совпадает с началом, называется нулевым. Нулевой вектор обозначается Очевидно, что длина нулевого вектора равна нулю: Определение 4. Векторы На рис. 3 приведены примеры сонаправленных векторов
Рис. 3
Определение 5. Векторы Если векторы Если векторы обозначены своими концами
Рис. 4 Рис. 5
Определение 5. Вектор Если вектор обозначен с помощью его концов
Действия над векторами В качестве действий над векторами, рассматриваются линейные операции – умножение вектора на число, сложение и вычитание. Умножение вектора на число Определение 6. Произведением вектора На рис. 6 – рис. 9 показаны пары векторы
Рис. 3. Случай
Рис. 4. Случай
Рис. 5. Случай
Рис. 6. Случай
Противоположный вектор
Отметим некоторые свойства умножения вектора на число.
1.
2.
3.
4. Теорема 1. Для коллинеарности векторов Сумма векторов Определение 7. Суммой векторов
Рис. 10
Отметим некоторые свойства суммы векторов.
1.
2.
3.
4. Разность векторов Определение 8. Разностью Разность Сумма и разность векторов определялись по правилу параллелограмма. Можно эти две операции определить по правилу треугольника. Для определения суммы
Рис. 11
Числовая ось Числовой осью (числовой прямой) называется любая прямая, если: 1) на ней выбрана некоторая точка, называемая началом (центром) и обозначаемая
2) любое из двух направлений, называемое положительным направлением и обозначаемое стрелкой;
3) некоторый отрезок, называемый единичным отрезком (масштабом).
Каждому вещественному числу на числовой прямой соответствует единственная точка на числовой оси: 1) положительное число 2) отрицательное число 3) нулевое число Имеет место и обратное соответствие: каждой точке на числовой оси соответствует единственное вещественное число. Пусть точке
Единичный вектор
Определение 9. Любой вектор, длина которой равна единице, называется единичным вектором. Пусть задан вектор
Для каждой числовой оси
Рис. 12
Угол между векторами Определение 10. Пусть векторы Из определения вытекает, что угол Определение 11. Пусть начало вектора
Рис. 13 Рис. 14 Проекция вектора на ось Определение 12. Проекцией точки
Рис. 15 Определение 13. Проекцией вектора
Рис. 16
Проекция вектора
Обозначим через
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.230.107 (0.23 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 на вещественное число
на вещественное число  называется вектор
называется вектор 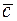 , коллинеарный вектору
, коллинеарный вектору 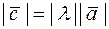 и сонаправленный с вектором
и сонаправленный с вектором  , и противонаправленный с вектором
, и противонаправленный с вектором 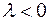 . Произведением вектора
. Произведением вектора  или
или  .
. ,
,  ,
,  ,
, 
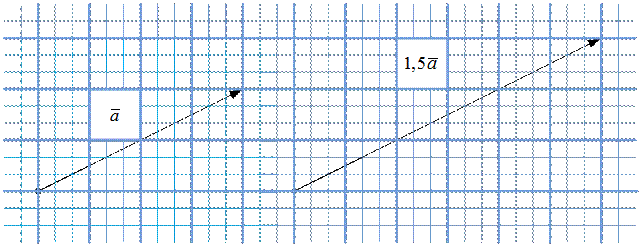






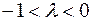
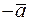 можно рассматривать как результат умножения вектора
можно рассматривать как результат умножения вектора  :
: .
.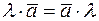 – закон коммутативности.
– закон коммутативности.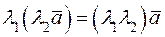 – закон ассоциативности.
– закон ассоциативности. – закон дистрибутивности.
– закон дистрибутивности.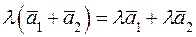 – закон дистрибутивности.
– закон дистрибутивности.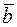 , необходимо и достаточно существование числа
, необходимо и достаточно существование числа  или
или  .
.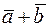 .
.
 – закон коммутативности.
– закон коммутативности. – закон ассоциативности.
– закон ассоциативности. .
. .
. векторов
векторов 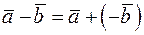 .
.
 ;
;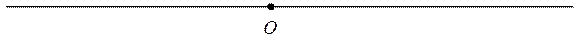


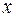 изображается точкой, расположенной на оси на расстоянии
изображается точкой, расположенной на оси на расстоянии 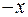 изображается точкой, расположенной на оси на расстоянии
изображается точкой, расположенной на оси на расстоянии  изображается началом оси.
изображается началом оси.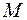 числовой оси соответствует число
числовой оси соответствует число  .
.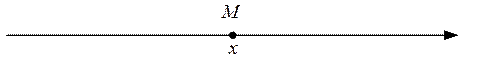
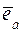 единичный вектор, сонаправленный с вектором
единичный вектор, сонаправленный с вектором  или
или 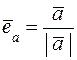 .
.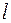 определен единичный вектор
определен единичный вектор 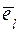 , с началом в точке
, с началом в точке 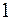 (рис. 12). Направление единичного вектора
(рис. 12). Направление единичного вектора 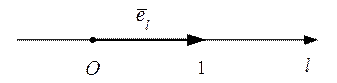
 , на который нужно повернуть один из этих векторов до совпадения с другим (рис. 13). Под термином совпадение понимается, что векторы
, на который нужно повернуть один из этих векторов до совпадения с другим (рис. 13). Под термином совпадение понимается, что векторы  .
.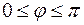 .
.
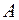 на ось
на ось 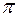 , проходящей через точку
, проходящей через точку 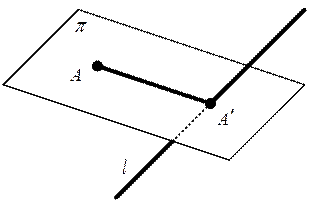
 на ось
на ось 
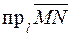 . Имеем
. Имеем .
.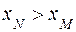 (рис 16), 2) отрицательной, если угол
(рис 16), 2) отрицательной, если угол 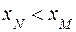 (рис. 17), 3) нулевой, если угол
(рис. 17), 3) нулевой, если угол  или
или 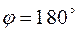 . В этом случае
. В этом случае 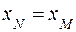 (рис. 18).
(рис. 18).
 .
.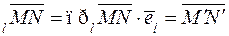 .
.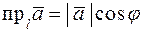 .
. .
. .
.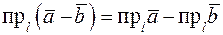 .
. – произвольный вектор. Длина вектора
– произвольный вектор. Длина вектора 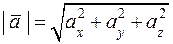 .
.
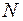 , то используется обозначение
, то используется обозначение 
 (аналогично,
(аналогично,  ).
). .
.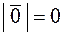 . У нулевого вектора направление не определено. В качестве направления нулевого вектора можно брать желаемое в данный момент направление.
. У нулевого вектора направление не определено. В качестве направления нулевого вектора можно брать желаемое в данный момент направление.
 .
. и
и 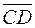 , то равенство
, то равенство  эквивалентно тому, что четырёхугольник
эквивалентно тому, что четырёхугольник  является параллелограммом (рис. 5).
является параллелограммом (рис. 5).
 .
. или
или  .
.


