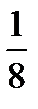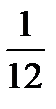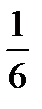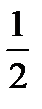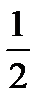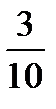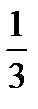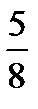Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные теоремы теории вероятностей. ⇐ ПредыдущаяСтр 4 из 4
Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, то есть Р(А+В)= Р(А)+Р(В) Следствие. Пусть события
Теорема сложения вероятностей совместных событий: Вероятность суммы двух совместных событий равна сумме вероятностей событий без вероятности их совместного появления, то есть Р(А+В)= Р(А)+Р(В) - Р(АВ) Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого (условной вероятностью события A при условии В называется вероятность события А найденная при условии, что событие В произошло, обозначается Р(А|В)) Р(АВ)= Р(В) Р(А|В)= Р(А)Р(В|А) Определение: События А и В называются независимыми если наступление одного из них не оказывает влияния на вероятность другого. Теорема умножения вероятностей независимых событий: Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий.
Р(АВ)= Р(А)Р(В). Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента. Дискретной назовём случайную величину, возможные значения которой образуют конечное множество. Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение, причём Определение: Математическим ожиданием случайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений. Математическое ожидание случайной величины X обозначается через MX. Если случайная величина X принимает значения Математическое ожидание часто называют средним значением случайной величины, так как оно указывает некоторое «среднее число», около которого группируются все значения случайной величины.
Определение: Пусть задан закон распределения случайной величины X:
Тогда такое распределение называется распределением Я. Бернулли или биноминальным распределением, причём верно равенство Определение: Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания. Дисперсия случайной величины X обозначается через DX. Следовательно, Пусть случайная величина X принимает значения
соответственно с вероятностями Поэтому математическое ожидание так распределённой случайной величины, то есть дисперсию X, можно записать в виде: Дисперсия случайной величины характеризует степень разброса, рассеивание случайной величины относительно её математического ожидания (среднего значения). Теорема 2. Дисперсия случайной величины равна математическому ожиданию квадрата этой величины без квадрата её математического ожидания, то есть
Вариант№0
Задание 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать? Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно N=n1´n2´n3=30´29´28=24360. Задание 2. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно Задание 3. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины? Решение. Элементарными исходами здесь являются наборы, включающие 3 фрукта. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов
Задание 4. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение. Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы
Задание 5. Монета подбрасывается 3 раза. Найти наиболее вероятное число успехов (выпадений герба). Решение. Возможными значениями для числа успехов в трех рассматриваемых испытаниях являются m = 0, 1, 2 или 3. Пусть Am - событие, состоящее в том, что при трех подбрасываниях монеты герб появляется m раз. По формуле Бернулли легко найти вероятности событий Am
Из этой таблицы видно, что наиболее вероятными значениями являются числа 1 и 2 (их вероятности равны 3/8). Этот же результат можно получить и из теоремы 2. Действительно, n=3, p=1/2, q=1/2. Тогда
Требования к содержанию отчета по работе Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
Контрольные вопросы (Задания для самопроверки качества освоенных результатов обучения): - определение вероятности события - теорема сложения вероятностей - теорема умножения вероятностей - понятие случайной величины - законом распределения случайной величины - формула математического ожидания и дисперсии случайной величины Приложение Задание 1. Задает ли закон распределения дискретной случайной величины данная таблица 1)
2)
3)
4)
5)
6)
7)
8)
9)
Задание 2. Дискретная случайная величина имеет закон распределения. Найти неизвестную вероятность. 1)
2)
3)
4)
5)
6)
8)
9)
Задание 3.
Задание 4. Вариант1 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. В лотерее разыгрывается 20000 билетов. Найдите математическое ожидание и дисперсию числа выигрышных билетов, если каждый билет может выигрышным с вероятностью 0,3. Вариант 2 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. В магазин поступила партия из 50 коробок с обувью черного и коричневого цвета. Найдите математическое ожидание и дисперсию числа коробок с обувью коричневого цвета, если вероятность того, что обувь будет коричневого цвета равна 0,2. Вариант 3 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа не взошедших семян из 800 посеянных семян данного растения, если каждое из семян может не взойти с вероятностью 0,01. Вариант 4 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. Найдите математическое ожидание и дисперсию числа студентов, которые не сдадут экзамен, в группе из 30 человек, если каждый студент может не сдать экзамен с вероятностью 0,4. Вариант 5 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. В урне находятся всего 100 белых и чёрных шаров. Найдите математическое ожидание и дисперсию числа белых шаров, если вероятность того, что шар будет белым равна 0,02. Вариант 6 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. Найдите математическое ожидание и дисперсию числа нестандартных ламп в партии из 300 ламп, если каждая лампа может оказаться нестандартной с вероятностью 0,07. Вариант 7 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. Найдите математическое ожидание и дисперсию числа фальшивых билетов, купленных на самолёт, в партии из 150 билетов, если каждый билет может оказаться фальшивым с вероятностью 0,004. Вариант 8 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 7000 деталей, если каждая деталь может оказаться со знаком качества с вероятностью 0,8. Вариант 9 1. Случайная величина X распределена по закону:
Найдите математическое ожидание и дисперсию случайной величины X. 2. Найдите математическое ожидание и дисперсию числа поддельных медицинских препаратов в партии из 126 препаратов, если каждый препарат может быть поддельным с вероятностью 0,06.
Список литературы Основные источники: 1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2014. Дополнительные источники: 2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015. 3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015. 4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://school-collection.edu.ru/catalog/– Загл. с экрана;
5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: http://window.edu.ru/– Загл. с экрана;
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-04-12; просмотров: 243; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.122.162 (0.063 с.) |
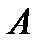 и
и 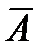 – противоположны. Сумма вероятностей противоположных событий равна единице, то есть
– противоположны. Сумма вероятностей противоположных событий равна единице, то есть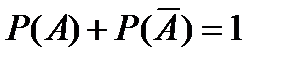 .
.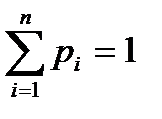 .
. соответственно с вероятностями
соответственно с вероятностями 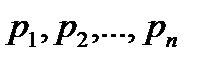 , то согласно определению:
, то согласно определению: . (1)
. (1)
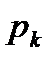
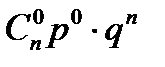
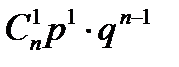
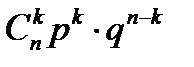
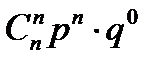
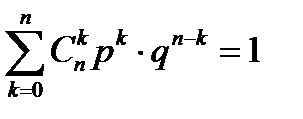 . (2)
. (2) 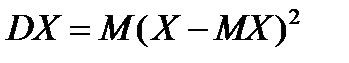 . (4)
. (4)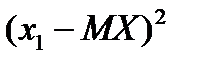 ,
,  , …,
, …,  , …,
, …, 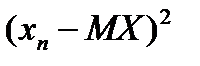
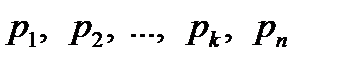 .
.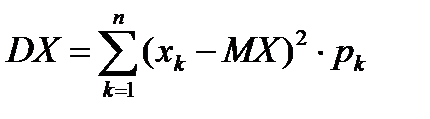 . (5)
. (5) . (6)
. (6)
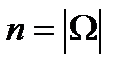 равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний
равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний 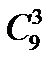 . Число благоприятствующих исходов
. Число благоприятствующих исходов 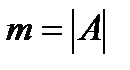 равно числу способов выбора 3 апельсинов из имеющихся 5, т.е.
равно числу способов выбора 3 апельсинов из имеющихся 5, т.е. 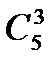 . Тогда искомая вероятность
. Тогда искомая вероятность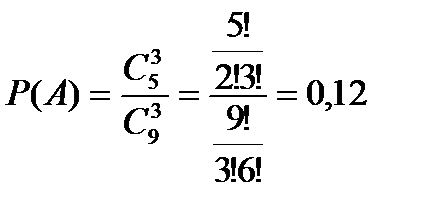 .
.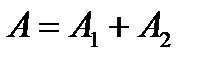 , где события
, где события 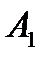 и
и  означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна
означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна  , а вероятность вытащить две синие пуговицы
, а вероятность вытащить две синие пуговицы 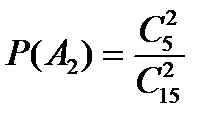 . Так как события
. Так как события 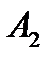 не могут произойти одновременно, то в силу теоремы сложения
не могут произойти одновременно, то в силу теоремы сложения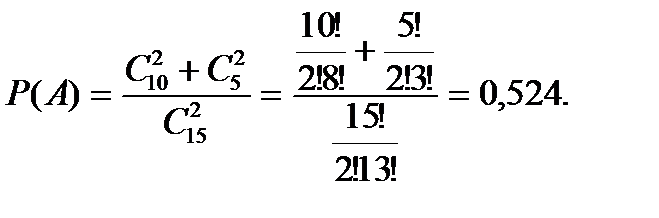
 , т.е.
, т.е.  .
.