
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Теоремы сложения и умножения вероятностей событийСодержание книги
Поиск на нашем сайте Тема 3. Теоремы сложения и умножения вероятностей событий Теорема умножения вероятностей независимых событий Определение. Два события называются независимыми, если появление (или непоявление) одного из них не меняет вероятность появления другого события (или непоявления). Пример. 1) Работа автоматических линий, которые не взаимосвязаны. А и В – остановки этих линий – независимые события. 2) Опыт состоит в бросании двух монет. События: Заметим, что вероятность события Теорема умножения вероятностей независимых событий Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:
Задача. Вероятность того, что потребитель увидит рекламу определенного продукта по телевидению, равна 0,06. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0,08. Предполагая, что оба события независимы, определить вероятность того, что потребитель увидит обе рекламы. Решение. Введем события:
События По условию задачи, вероятности Нужно найти вероятность В наших обозначениях событие Ответ: Зависимые события. Условная вероятность. Теорема умножения вероятностей зависимых событий Определения. Событие Вероятность того, что произошло событие Пример. Пример зависимых событий. В ящике 2 белых шара и 4 черных шара. Из ящика вынимают один шар (первое вынимание), затем второй шар (второе вынимание). События: Очевидно, что вероятность события
Вероятность события
Видим, что
Пример. 1) Несовместные события – это, например, пара противоположных событий: · А – выпал орел, В – выпала решка; · А – выпало 5 очков, В – выпало любое число очков, кроме 5; · А – наступилохотя бы одно из событий А1, А2; В – не наступило ни одно из событий А1, А2.
Тема 3. Теоремы сложения и умножения вероятностей событий
|
||
|
Последнее изменение этой страницы: 2021-04-04; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

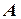 – появление герба на первой монете;
– появление герба на первой монете; 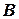 – появление герба на второй монете.
– появление герба на второй монете.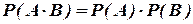 .
.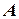 - потребитель увидит рекламу по телевидению;
- потребитель увидит рекламу по телевидению;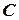 - потребитель увидит обе рекламы;
- потребитель увидит обе рекламы; - потребитель увидит хотя бы одну рекламу.
- потребитель увидит хотя бы одну рекламу.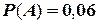 ;
; 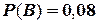 .
.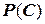 .
.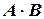 . Поскольку события
. Поскольку события 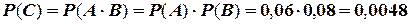 .
. .
.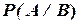 и называть условной вероятностью события
и называть условной вероятностью события 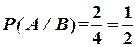 .
.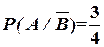 .
.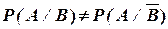 .
.


