Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выписка из лицевого счета Маши.ВАРИАНТ 6 Задание 1 № 26637 На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? Решение. Разделим 500 на 30:
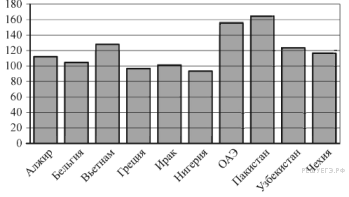
Ване хватает денег на 16 тюльпанов, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 15 тюльпанов. Ответ: 15. Задание 2 № 501738 На диаграмме показано распределение выбросов углекислого газа в атмосферу в 10 странах мира (в миллионах тонн) за 2008 год. Среди представленных стран первое место по объёму выбросов занимал Пакистан, десятое место — Нигерия. Какое место среди представленных стран занимала Чехия?
Решение. Расположим страны в порядке убывания количества выбросов углекислого газа в год:
1) Пакистан 2) ОАЭ 3) Вьетнам 4) Узбекистан 5) Чехия 6) Алжир 7) Бельгия 8) Ирак 9) Греция 10) Нигерия Чехия находится на пятом месте Ответ: 5. Задание 3 № 245007
Площадь четырёхугольника состоит из площадей двух треугольников и площади трапеции. Поэтому
Ответ:4,5 см2. Задание 4 № 320189 В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных. Решение. Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна
Ответ: 0,498. Задание 5 № 26661 Найдите корень уравнения Решение. Возведем в квадрат:
Ответ: 35.
Найдите большую диагональ ромба, сторона которого равна Решение. Тупой угол ромба равен 180°−60°=120°. Воспользуемся теоремой косинусов:
Ответ: 3. Задание 7 № 27500
Решение. Если функция непрерывна на отрезке [ a; b ], а её производная положительна (отрицательна) на интервале (a; b), то функция возрастает (убывает) на отрезке [ a; b ]. Производная функции отрицательна, на интервалах (−1; 5) и (7; 11). Значит, функция убывает на отрезках [−1; 5] длиной 6 и [7; 11] длиной 4. Длина наибольшего из них 6. Ответ: 6.
Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1, правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Площадь основания четырехугольной призмы равна двум третьим площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
Ответ: 8. Задание 9 № 26776 Найдите Решение. Поскольку угол альфа лежит в третьей четверти, его тангенс положителен. Поэтому
Тогда
Ответ: 5. Задание 10 № 319859 Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-5
Ответ:35. Задание 11 № 99588 Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? Решение. Пусть t ч – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние 65 t км, а второй – 75 t км. Тогда имеем:
Таким образом, автомобили встретятся через 4 часа. Ответ: 4. Задание 12 № 77468 Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
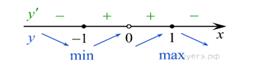
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: −1. Задание 13 (С1) № 507595
а) Решите уравнение б) Найдите корни этого уравнения, принадлежащие промежутку Решение. а) Преобразуем уравнение:
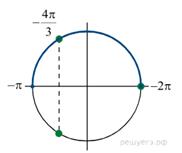
б) Отберём с помощью единичной окружности корни уравнения, принадлежащие промежутку Ответ: а) Задание 14 (С2) № 513684
*Критерии распространяются и на случай использования координатного метода В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 точка K делит боковое ребро AA 1 в отношении AK: KA 1 = 1: 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD 1 в точке M. а) Докажите, что плоскость α делит ребро DD 1 в отношении DM: MD 1 = 2: 1. б) Найдите площадь сечения, если известно, что AB = 4, AA 1 = 6.
Пусть четырёхугольник KBNM — сечение данной призмы плоскостью α (см. рисунок). Прямая AC параллельна плоскости α, а плоскость ACK пересекает плоскость α по прямой KN, следовательно, KN || AC и, значит, AKNC — прямоугольник. Прямые BD и AC являются соответственно проекциями прямых BM и KN на плоскость ABC, значит, точка пересечения прямых BD и AC (точка H) является проекцией точки пересечения прямых BM и KN (точки O) на эту плоскость. Таким образом, C другой стороны, отрезок OH — средняя линия треугольника BDM и, следовательно, б) Так как
Ответ: б) Задание 15 (С3) № 484584
Решите неравенство Решение. Разделим обе части неравенства на
При этих условиях получаем неравенство:
Таким образом, множество решений исходного неравенства:
Ответ: Задание 16 (С4) № 512338
Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN. а) Докажите, что четырёхугольник NQOH — параллелограмм. б) Найдите KN, если ∠ LKN = 75° и LM = 1.
а) б) Пусть окружность с центром в точке O радиуса R касается стороны MN в точке P. В прямоугольных треугольниках OPQ и KHL имеем
Поэтому
Пусть KH = x. Поскольку трапеция KLMN равнобедренная, KN = 2 KH + + LM, NH = KH + LM = x + 1. Тогда
Откуда x = 1. Значит, KN = 2 x + 1 = 3. Ответ: б) 3. Задание 17 (С5) № 511255
Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей? Решение. Пусть для определённости Миша и Маша 15.01.12 положили в банк x рублей. Подготовим выписки из лицевых счетов Маши и Миши. Задание 18 (С6) № 513610
Найдите все значения a, при каждом из которых система уравнений
имеет ровно два различных решения.
Графическое решение. Запишем первое уравнение системы в виде
При Число решений исходной системы равно числу точек пересечения прямой у = 2 и гиперболы Прямая Таким образом, исходная система имеет ровно два решения при Аналитическое решение. Запишем первое уравнение системы в виде
Тогда исходная система равносильна следующей:
При a = 0 система решений не имеет. В противном случае, первое уравнение имеет корень Ответ: Примечание. Полезно сравнить это задание с аналогичной задачей досрочного ЕГЭ 2015 года: найдите все значения параметра a, при каждом из которых система уравнений
имеет единственное решение. Задание 19 (С7) № 525144
Вася и Петя решали задачи из сборника, причем каждый следующий день Вася решал на одну задачу больше, чем в предыдущий, а Петя — на две задачи больше, чем в предыдущий. В первый день каждый решил хотя бы одну задачу, а в итоге каждый решил все задачи сборника. а) Могло ли быть в сборнике 85 задач? б) Могло ли быть в сборнике 213 задач, если каждый из мальчиков решал их более трех дней? в) Какое наибольшее количество дней мог решать задачи Петя, если Вася решил весь сборник за 16 дней, а количество задач в сборнике меньше 300. Решение. Пусть Вася в первый день решил a задач, а Петя — b задач. Вася решал задачи n дней, а Петя — m дней. Воспользуемся формулой суммы арифметической прогрессии. Получим, что за n дней Вася решил а) Проверим, могли ли мальчики решить 85 задач. Для Васи:
Для Пети: Значит, в сборнике могло быть 85 задач. б) Проверим, могло ли в сборнике быть 213 задач, если каждый из мальчиков решал их более трех дней. Для Пети: в) Если в сборнике меньше 300 задач, то для числа дней, потраченных Петей, имеем: При Рассмотрим Рассмотрим Рассмотрим При этом Таким образом, все условия задачи выполнены. Ответ: а) да, б) нет, в) 14.
ВАРИАНТ 6 Задание 1 № 26637 На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Вани есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Маше на день рождения? Решение. Разделим 500 на 30:
Ване хватает денег на 16 тюльпанов, но цветов должно быть нечетное число. Следовательно, Ваня может купить букет из 15 тюльпанов. Ответ: 15. Задание 2 № 501738 На диаграмме показано распределение выбросов углекислого газа в атмосферу в 10 странах мира (в миллионах тонн) за 2008 год. Среди представленных стран первое место по объёму выбросов занимал Пакистан, десятое место — Нигерия. Какое место среди представленных стран занимала Чехия?
Решение. Расположим страны в порядке убывания количества выбросов углекислого газа в год:
1) Пакистан 2) ОАЭ 3) Вьетнам 4) Узбекистан 5) Чехия 6) Алжир 7) Бельгия 8) Ирак 9) Греция 10) Нигерия Чехия находится на пятом месте Ответ: 5. Задание 3 № 245007
Площадь четырёхугольника состоит из площадей двух треугольников и площади трапеции. Поэтому
Ответ:4,5 см2. Задание 4 № 320189 В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных. Решение. Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна
Ответ: 0,498. Задание 5 № 26661 Найдите корень уравнения Решение. Возведем в квадрат:
Ответ: 35.
Найдите большую диагональ ромба, сторона которого равна Решение. Тупой угол ромба равен 180°−60°=120°. Воспользуемся теоремой косинусов:
Ответ: 3. Задание 7 № 27500
Решение. Если функция непрерывна на отрезке [ a; b ], а её производная положительна (отрицательна) на интервале (a; b), то функция возрастает (убывает) на отрезке [ a; b ]. Производная функции отрицательна, на интервалах (−1; 5) и (7; 11). Значит, функция убывает на отрезках [−1; 5] длиной 6 и [7; 11] длиной 4. Длина наибольшего из них 6. Ответ: 6.
Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1, правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.
Площадь основания четырехугольной призмы равна двум третьим площади основания правильной шестиугольной призмы, а высота у них общая. Поэтому
Ответ: 8. Задание 9 № 26776 Найдите Решение. Поскольку угол альфа лежит в третьей четверти, его тангенс положителен. Поэтому
Тогда
Ответ: 5. Задание 10 № 319859 Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Q. Каждый отдельный показатель оценивается читателями по 5-5
Ответ:35. Задание 11 № 99588 Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч? Решение. Пусть t ч – время движения автомобилей до встречи. Первый автомобиль пройдет расстояние 65 t км, а второй – 75 t км. Тогда имеем:
Таким образом, автомобили встретятся через 4 часа. Ответ: 4. Задание 12 № 77468 Найдите точку минимума функции Решение. Найдем производную заданной функции:
Найдем нули производной:
Определим знаки производной функции и изобразим на рисунке поведение функции:
Искомая точка минимума Ответ: −1. Задание 13 (С1) № 507595
а) Решите уравнение б) Найдите корни этого уравнения, принадлежащие промежутку Решение. а) Преобразуем уравнение:
б) Отберём с помощью единичной окружности корни уравнения, принадлежащие промежутку Ответ: а) Задание 14 (С2) № 513684
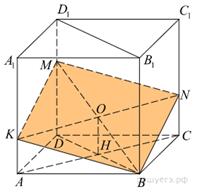
*Критерии распространяются и на случай использования координатного метода В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 точка K делит боковое ребро AA 1 в отношении AK: KA 1 = 1: 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD 1 в точке M. а) Докажите, что плоскость α делит ребро DD 1 в отношении DM: MD 1 = 2: 1. б) Найдите площадь сечения, если известно, что AB = 4, AA 1 = 6.
Пусть четырёхугольник KBNM — сечение данной призмы плоскостью α (см. рисунок). Прямая AC параллельна плоскости α, а плоскость ACK пересекает плоскость α по прямой KN, следовательно, KN || AC и, значит, AKNC — прямоугольник. Прямые BD и AC являются соответственно проекциями прямых BM и KN на плоскость ABC, значит, точка пересечения прямых BD и AC (точка H) является проекцией точки пересечения прямых BM и KN (точки O) на эту плоскость. Таким образом, C другой стороны, отрезок OH — средняя линия треугольника BDM и, следовательно, б) Так как
Ответ: б) Задание 15 (С3) № 484584
Решите неравенство Решение. Разделим обе части неравенства на
При этих условиях получаем неравенство:
Таким образом, множество решений исходного неравенства:
Ответ: Задание 16 (С4) № 512338
Дана равнобедренная трапеция KLMN с основаниями KN и LM. Окружность с центром O, построенная на боковой стороне KL как на диаметре, касается боковой стороны MN и второй раз пересекает большее основание KN в точке H, точка Q — середина MN. а) Докажите, что четырёхугольник NQOH — параллелограмм. б) Найдите KN, если ∠ LKN = 75° и LM = 1.
а) б) Пусть окружность с центром в точке O радиуса R касается стороны MN в точке P. В прямоугольных треугольниках OPQ и KHL имеем
Поэтому
Пусть KH = x. Поскольку трапеция KLMN равнобедренная, KN = 2 KH + + LM, NH = KH + LM = x + 1. Тогда
Откуда x = 1. Значит, KN = 2 x + 1 = 3. Ответ: б) 3. Задание 17 (С5) № 511255
Миша и Маша положили в один и тот же банк одинаковые суммы под 10% годовых. Через год сразу после начисления процентов Миша снял со своего счета 5000 рублей, а еще через год снова внес 5000 рублей. Маша, наоборот, через год доложила на свой счет 5000 рублей, а еще через год сразу после начисления процентов сняла со счета 5000 рублей. Кто через три года со времени первоначального вложения получит большую сумму и на сколько рублей? Решение. Пусть для определённости Миша и Маша 15.01.12 положили в банк x рублей. Подготовим выписки из лицевых счетов Маши и Миши. Выписка из лицевого счета Маши.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.012 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

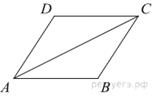
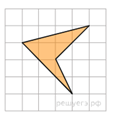 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Решение.
Решение.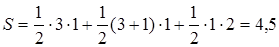 см2.
см2.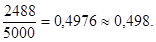
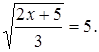
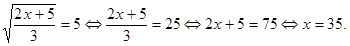
 Задание 6 № 27828
Задание 6 № 27828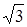 , а острый угол равен 60°.
, а острый угол равен 60°.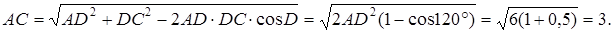
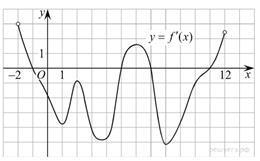 На рисунке изображен график производной функции f(x), определенной на интервале (−2;12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
На рисунке изображен график производной функции f(x), определенной на интервале (−2;12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.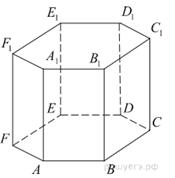 Задание 8 № 245345
Задание 8 № 245345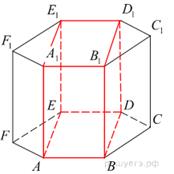 Решение.
Решение.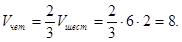
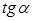 , если
, если 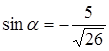 и
и 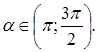
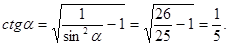
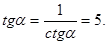

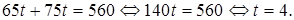
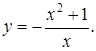
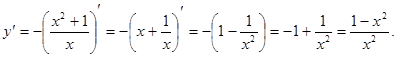
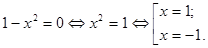
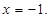
 .
.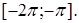

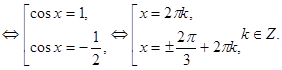
 :
: 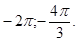
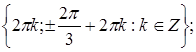 б)
б) 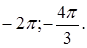
 Решение.
Решение. .
.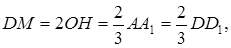 откуда и следует доказываемое утверждение.
откуда и следует доказываемое утверждение.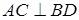 и
и 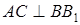 , то
, то  Но KN || AC, значит, и
Но KN || AC, значит, и  . Следовательно,
. Следовательно, 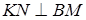 , поскольку
, поскольку 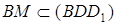 и площадь сечения S равна
и площадь сечения S равна 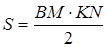 . Имеем:
. Имеем: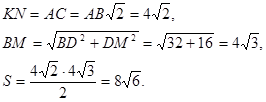
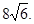
 .
.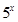 .
.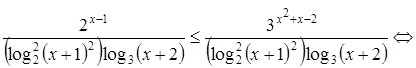

 Решение будем искать при условиях
Решение будем искать при условиях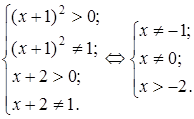

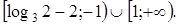
 Решение.
Решение.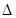 KOH равнобедренный, и трапеция KLMN равнобедренная, поэтому ∠ KHO = ∠ OKH = ∠ MNK. Значит, прямые OH и MN параллельны, а так как OQ — средняя линия трапеции, то параллельны прямые OQ и KN. Противоположные стороны четырёхугольника NQOH попарно параллельны, следовательно, NQOH — параллелограмм.
KOH равнобедренный, и трапеция KLMN равнобедренная, поэтому ∠ KHO = ∠ OKH = ∠ MNK. Значит, прямые OH и MN параллельны, а так как OQ — средняя линия трапеции, то параллельны прямые OQ и KN. Противоположные стороны четырёхугольника NQOH попарно параллельны, следовательно, NQOH — параллелограмм.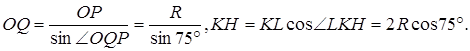
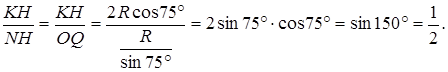
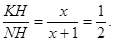
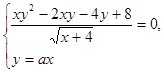
 Решение.
Решение.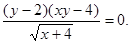
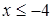 левая часть не имеет смысла. При
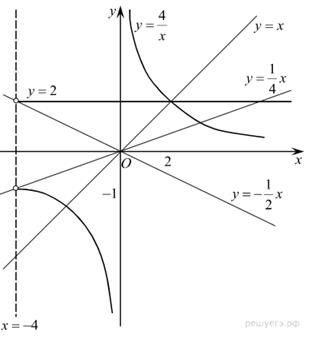
левая часть не имеет смысла. При  уравнение задаёт прямую у = 2 и гиперболу
уравнение задаёт прямую у = 2 и гиперболу 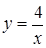 (см. рис.). При каждом значении a уравнение
(см. рис.). При каждом значении a уравнение 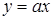 задаёт прямую с угловым коэффициентом a, проходящую через начало координат.
задаёт прямую с угловым коэффициентом a, проходящую через начало координат.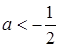 и при
и при  ; пересекает правую ветвь гиперболы при
; пересекает правую ветвь гиперболы при 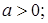 пересекает левую ветвь гиперболы при
пересекает левую ветвь гиперболы при 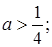 проходит через точку пересечения прямой у = 2 и гиперболы при
проходит через точку пересечения прямой у = 2 и гиперболы при 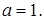
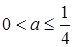 и при
и при 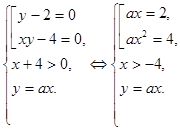
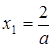 , который удовлетворяет системе при
, который удовлетворяет системе при 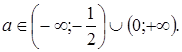 Второе уравнение имеет два различных корня
Второе уравнение имеет два различных корня 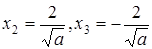 только при a > 0, причем, x 2 является корнем системы при любом положительном a, а x 3 при
только при a > 0, причем, x 2 является корнем системы при любом положительном a, а x 3 при 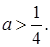 Таким образом, система будет иметь два различных решения при
Таким образом, система будет иметь два различных решения при 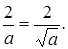 Это происходит при a = 1.
Это происходит при a = 1.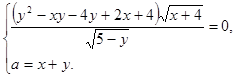
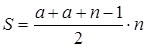 задач, а Петя за m дней решил
задач, а Петя за m дней решил  задач.
задач.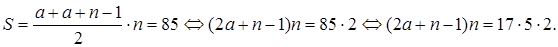 Очевидно, что это уравнение имеет решения в натуральных числах. Например,
Очевидно, что это уравнение имеет решения в натуральных числах. Например, 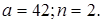
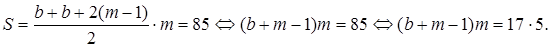 Очевидно, что и это уравнение имеет решения в натуральных числах. Например,
Очевидно, что и это уравнение имеет решения в натуральных числах. Например, 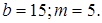
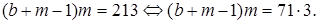 Тогда m — один из делителей числа 213. Заметим, что 71 — простое число, и по условию
Тогда m — один из делителей числа 213. Заметим, что 71 — простое число, и по условию  Тогда или
Тогда или 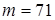 , или
, или  При любом из этих значений получаем
При любом из этих значений получаем  Значит, в сборнике не могло быть 213 задач.
Значит, в сборнике не могло быть 213 задач.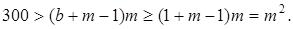 Следовательно,
Следовательно, 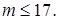
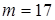 получаем
получаем 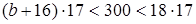 тогда
тогда 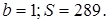 Проверим, мог ли Вася за 16 дней решить 289 задач:
Проверим, мог ли Вася за 16 дней решить 289 задач: 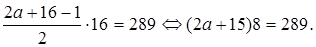 Левая часть уравнения кратна 8, а правая нет, значит, m не может равняться 17.
Левая часть уравнения кратна 8, а правая нет, значит, m не может равняться 17.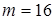 . Имеем
. Имеем 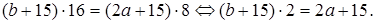 Левая часть уравнения кратна 2, а правая нет. Значит, m не может равняться 16.
Левая часть уравнения кратна 2, а правая нет. Значит, m не может равняться 16.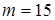 . Имеем
. Имеем 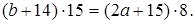 Левая часть уравнения кратна 15 при
Левая часть уравнения кратна 15 при  , но тогда
, но тогда  . Значит, m не может равняться 15.
. Значит, m не может равняться 15.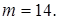 Имеем
Имеем 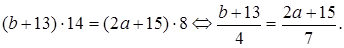 Это уравнение имеет решение
Это уравнение имеет решение