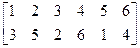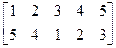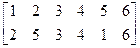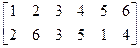Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шифрование данных методами подстановки, перестановки и полиалфавитными шифрамиСодержание книги
Поиск на нашем сайте
ЗАДАНИЕ № 1. ШИФРОВАНИЕ ДАННЫХ МЕТОДАМИ ПОДСТАНОВКИ, ПЕРЕСТАНОВКИ И ПОЛИАЛФАВИТНЫМИ ШИФРАМИ Цель работы: Приобретение навыков шифрования информации с использованием простейших методов шифрования.
Теоретические основы криптографии Проблемой защиты информации путем ее преобразования занимается криптология (kryptos - тайный, logos - наука). Криптология разделяется на два направления - криптографию и криптоанализ. Цели этих направлений прямо противоположны: - криптография занимается поиском и исследованием математических методов преобразования информации. - сфера интересов криптоанализа - исследование возможности расшифровывания информации без знания ключей.
1.1.1. Терминология
Криптография дает возможность преобразовать информацию таким образом, что ее прочтение (восстановление) возможно только при знании ключа. В качестве информации, подлежащей шифрованию и дешифрованию, рассматриваются тексты, построенные на некотором алфавите. Под этими терминами понимается следующее: Алфавит - конечное множество используемых для кодирования информации знаков. Текст - упорядоченный набор из элементов алфавита. В качестве примеров алфавитов, используемых в современных информационных системах, можно привести следующие: - алфавит Z33 - 32 буквы русского алфавита и пробел; - алфавит Z256 - символы, входящие в стандартные коды ASCII и КОИ-8; - бинарный алфавит - Z2 = {0,1}; - восьмеричный алфавит или шестнадцатеричный алфавит; Шифрование - преобразовательный процесс: исходный текст, который носит также название открытого текста, заменяется шифрованным текстом. Дешифрование - обратный шифрованию процесс. На основе ключа шифрованный текст преобразуется в исходный. Ключ - информация, необходимая для беспрепятственного шифрования и дешифрования текстов. Обычно ключ представляет собой последовательный ряд символов того же алфавита, в котором набрано информационное сообщение
Классификация криптографических методов
По характеру используемого ключа криптографические методы делятся на: - симметричные: для шифрования и дешифрования используется один и тот же секретный ключ; - асимметричные: для шифрования и дешифрования используют разные ключи, открытый – для шифрования, секретный – для дешифрования.
К симметричным криптографическим алгоритмам относят простейшие методы шифрования (подстановки, перестановки), потоковые и блочные шифры.
Обзор используемых методов Метод подстановки
Наиболее простой вид преобразований, заключающийся в замене символов исходного текста на другие символы того же либо другого алфавита по более или менее сложному правилу. Историческим примером шифра подстановки (замены) является шифр Цезаря, в котором каждый символ открытого текста заменяется другой буквой, которая определяется путем смещения по алфавиту от исходной буквы влево или вправо на k букв. При достижении конца алфавита выполняется циклический переход к его началу. Цезарь использовал шифр замены при смещении вправо при k = 3. Для произвольного ключа k шифр имеет вид:
где А – символ открытого текста, В – заменяющий символ, i – номер буквы в алфавите, n –количество букв в алфавите. Обратная подстановка осуществляется по правилу
Условием для успешной реализации этого метода является совпадение размера множеств открытого текста и шифротекста. Это условие в современных криптосистемах называется гомоморфизмом. Другим вариантом метода подстановки является задание соответствия между буквами исходного алфавита и буквами подстановочного алфавита. Это позволяет заменять буквы в открытом тексте буквами из подстановочного алфавита Подстановочный алфавит может задаваться как множество символов, либо составляться по определенному правилу. Пусть подстановочный алфавит составлен по следующему правилу: А (2 k -1)= В (2 k); А (2 k)= В (33-2 k), (1.4) где А - исходный перестановочный алфавит; В - подстановочный алфавит; 1£ k £ 16. Формула 1.3 используется для замены букв с нечетными номерами в алфавите, формула 1.4 - для замены букв с четными номерами. Воспользуемся новым алфавитом для шифрования фразы:
ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ Каждая буква в этой фразе имеет порядковый номер в исходном алфавите. При шифровании методом подстановки необходимо заменить буквы исходного алфавита соответствующими буквами подстановочного алфавита (О - П, С - О, Н - Т и т.д.). Так буква О в исходном алфавите имеет номер 16, k =8. По правилу А (2×8)= В (33-2×8) буква О заменяется буквой с номером 17, т.е. П. В шифрованном виде эта фраза примет следующий вид: ПОТПГЭ ШБЖЙУЭ ЙТХПСНБЧЙЙ. Шифрование простой подстановкой на коротких алфавитах обеспечивает слабую защиту открытого текста. Подстановочные криптограммы можно раскрыть, составляя частотные таблицы для букв, пар букв (биграмм) и троек букв (триграмм). Большие частоты появления одних букв и малые других, а также частые ассоциации гласных с согласными позволяют найти буквы открытого текста. С увеличением размера алфавита применение частотного анализа становится все более дорогим, однако, принцип подстановки теряет свою практическую значимость.
Метод перестановки Также несложный метод криптографического преобразования. Используется, как правило, в сочетании с другими методами. При шифровании этим методом переставляются не буквы алфавита, а буквы открытого текста. Например, сообщение разбито на 4 группы знаков, включая пробелы, и в каждой группе буквы переставлены в соответствии с правилом: é1 2 3 4 ù ë2 4 1 3û В этом случае фраза: ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ будет представлена в следующем виде: СООНЫЗВ ЩТАИ НЫИОМФРИАИ. В случае перестановки таблицы частот для пар и трех букв показывают наличие стандартных буквенных пар, позволяя реконструировать открытый текст путем поиска тех перестановок, которые их воссоединяют. Следовательно, ключ, используемый для преобразования открытого текста, может быть восстановлен по одной криптограмме.
Многоалфавитные шифры Слабая криптостойкость моноалфавитных подстановок преодолевается с применением подстановок многоалфавитных. Для защиты от частотного анализа были разработаны многоалфавитные шифры, в которых для шифрования сообщения периодически используется несколько различных подстановочных алфавитов. Если задано r подстановочных алфавитов, то исходное сообщение разбивается на группы по r символов, для шифрования i -го символа группы используется i -ый подстановочный алфавит. Например, для r =4 буквы с номерами 1,5,9,13,... шифруются 1 алфавитом, буквы с номерами 2,7,10,14,... - 2 алфавитом, и т.д. Для получения открытого текста выделяются повторяющиеся группы знаков, и определяется период повторения. Предполагаемый период проверяется составлением частотного распределения для каждой n-й буквы зашифрованного текста. Если каждое из n частотных распределений имеет сильную неоднородность, характерную для моноалфавитной подстановки, то предполагаемый период является правильным. Затем задача решается как n различных простых подстановок.
Задание на лабораторную работу
1. Разработать алгоритм и составить программу, позволяющую закодировать любой текст одним из вышеизложенных методов и выполнить обратное преобразование. Метод, которым необходимо зашифровать исходную информацию, выбирается в соответствии с вариантом из таблиц 1.1, 1.2, 1.3. Язык программирования выбирается произвольно.
2. Осуществить вывод на экран или принтер полученной криптограммы. 3. Провести дешифрование данной криптограммы, в результате должен быть получен исходный текст. 4. Результаты работы оформить в виде отчета. 5. Содержание отчета: - описание используемого метода, - описание исходных данных, - алгоритм работы программы, - текст программы, - результаты работы программы, - анализ результатов - выводы.
Варианты индивидуальных заданий Таблица 1.1 - Методы шифрования
Таблица 1.2 – Подстановочные алфавиты
Таблица 1.3 - Группы перестановок
1.5. Контрольные вопросы 1. Почему метод подстановки имеет слабую надежность? 2. Что такое частотный анализ? 3. Что является криптографическим ключом в методе перестановки? ЗАДАНИЕ №2. Задание на лабораторную работу 1. Выбрать в таблице параметры генератора ПСЧ: A, C, T(0), b. 2. Разработать программу шифрования и дешифрования текста. 3. Произвести шифрование исходного текста, получить шифрограмму, осуществить ее дешифрование и сравнение с исходным текстом. 4. Произвести изменение одного или несколько параметров генератора случайных чисел, осуществить получение шифрограммы и сравнение ее с предыдущим вариантом. 5. Результаты работы оформить в виде отчета. 6. Содержание отчета: - описание используемого метода, - описание исходных данных, - алгоритм работы программы, - текст программы, - результаты работы программы, - анализ результатов - выводы.
Варианты индивидуальных заданий Таблица 2.1 – Генераторы ПСЧ
2.5. Контрольные вопросы
1. Какие параметры конгруэнтного генератора необходимо выбрать для получения максимальной длины последовательности псевдослучайных чисел? 2. От чего зависит длина псевдослучайной последовательности? 3. Принцип действия генераторов с обратной связью? 4. Какие стандарты используют методы гаммирования? ЗАДАНИЕ № 3. СЕТИ ФЕЙШТЕЛЯ
Цель работы:изучить принципы работы сети Фейштеля, научиться шифровать информацию посредством использования блочного криптоалгоритма.
Задание на лабораторную работу 1. Выбрать в таблице параметры для сети Фейштеля 2. Разработать программу шифрования и дешифрования текста. 3. Произвести шифрование исходного текста, получить шифрограмму, осуществить ее дешифрование и сравнение с исходным текстом. 4. Результаты работы оформить в виде отчета. 5. Содержание отчета: - описание используемого метода, - описание исходных данных, - алгоритм работы программы, - текст программы, - результаты работы программы, - анализ результатов - выводы. Варианты индивидуальных заданий Варианты заданий представлены в таблице 3.1. номер варианта выбирается в соответствии с номером студента в списке группы.
Таблица 3.1 – Параметры сети Фейштеля
3.4 Контрольные вопросы 1. Какова структура классической сети Фейштеля? 2. Что называется раундом в сети Фейштеля? 3. Какими свойствами обладает сеть Фейштеля? 4. Каким образом используется материал ключа при шифровании?
ЗАДАНИЕ №4. ИЗУЧЕНИЕ АЛГОРИТМОВ RSA
Цель работы: Освоить механизм шифрования и дешифрования данных в криптографической системе с открытыми ключами RSA.
Криптосистема RSA
RSA – криптографическая система с открытым ключем, обеспечивающая такие механизмы защиты как шифрование и цифровая подпись (аутентификация – установление подлинности). Алгоритм RSA работает следующим образом: Пусть p и q - два больших различных простых числа, и пусть n = p × q и e некоторое целое, взаимно простое с (p -1)×(q -1). Пространства открытых текстов Mk и зашифрованных сообщений Ck представляют собой множество неотрицательных целых чисел Zn, меньших n. Если исходное сообщение окажется слишком длинным, чтобы принадлежать Zn, его необходимо разбить на части, равные m. Соответствующая ключу k функция шифрования Ek: Mk -> Ck определяется как Ek (m) = m e mod(n). Для того, чтобы полностью определить алгоритм ее вычисления, достаточно записать e и n в открытый справочник. Такая пара называется открытым ключом. Ek является кандидатом на однонаправленную функцию с потайным ходом, и хотя существует эффективный алгоритм вычисления обратной ей функции Dk, мы не знаем, как получить его на основании алгоритма Ek (т.е. только для заданных n и e). Эффективный алгоритм вычисления Dk легко получить, задав дополнительную секретную информацию p и q. С этой целью, используя обобщенные алгоритмы Евклида для нахождения наибольшего общего делителя, чтобы вычислить целое число d, такое что e × d = 1 mod ф (n), где ф (n) = (p -1)× (q -1) – функция Эйлера. По теореме Эйлера m (ed) = m mod(n) для любого целого числа m и, следовательно, (m e) d mod(n) = m, при условии что 0 <= m < n, что обеспечивается, когда m принадлежит Mk. Функция дешифрования Dk: Ck -> Mk в связи с этим определяется как Dk (c) = с d mod(n), и эффективный алгоритм для модульного возведения в степень также может быть использован и для ее вычисления. Тогда каждый пользователь криптосистемы RSA должен выбрать целые числа p, q и e и вычислить с их помощью d. После чего он делает свой открытый ключ доступным в пользовательском справочнике, тогда как d сохраняет в секрете. Это дает возможность любому другому пользователю шифровать посылаемые ему сообщения, которые только он и может расшифровать. Для того чтобы эта идея была реализована практически, решающим является удовлетворение требование, чтобы генерация больших случайных простых чисел и вычисление d были легко осуществимы. Например, пусть p = 19 и q = 23, тогда n = 437 и ф (n) = 396. Пусть также e = 13, и поэтому d = 61, так как 13×61 = 793 = 2 ф (n)+1. Тогда сообщение в открытом текcте m = 123 будет зашифровано как c = 12313 mod(437) = 386. Действительно, 38661 mod(437) = 123. Если бы существовали эффективные методы разложения на сомножители (факторинга), то, разложив n на сомножители (факторы) p и q, можно было бы получить секретный (private) ключ d. Таким образом надежность криптосистемы RSA основана на трудноразрешимой задаче разложения n на сомножители (то есть на невозможности факторинга n) так как в настоящее время эффективного способа поиска сомножителей не существует.
4.1.2. Алгоритм шифрования и дешифрования RSA.
1. Выберем два больших простых p и q. 2. Определим n = p × q. 3. Выберем большое случайное число, которое назовем e. Это число должно быть взаимно простым с результатом (p -1)×(q -1). 4. Определим такое число d, для которого является истинным соотношение (e × d) mod((p -1)×(q -1))=1. 5. Назовем открытым ключом числа e и n, а секретным ключом - числа d, p и q. После произведенного выбора открытого и секретного ключей по вышеизложенному алгоритму для шифрования данных необходимо выполнить следующие действия: - разбить шифруемый текст на блоки, каждый из которых может быть представлен в виде числа М (i)= 0,1,..., n -1; - зашифровать текст, рассматриваемый как последовательность чисел M (i) по формуле: C (i) = (M (i)e)mod n; (4.1) Чтобы расшифровать эти данные, используется секретный ключ { d, n } и выполняются следующие вычисления: M (i) = (C (i)d) mod n. (4.2) В результате получают исходный текст M (i).
Задание на лабораторную работу
1. Разработать программу, осуществляющую шифрование и дешифрование алгоритмом RSA. 2. Исходное открытое сообщение М должно состоять не менее, чем из 2 n символов. Допускается использование как русского, так и любого другого алфавита для написания исходного текста. 3. Зашифрованный текст оформить в виде самостоятельного файла. 4. В программе предусмотреть проверку, являются ли два числа взаимно простыми. 5. Результаты работы оформить в виде отчета. 6. Содержание отчета: - описание используемого метода, - описание исходных данных, - алгоритм работы программы, - текст программы, - результаты работы программы, - анализ результатов - выводы.
4.3. Контрольные вопросы
1. Что такое однонаправленные функции? 2. Основные свойства однонаправленных функций с потайным ходом? 3. Какие криптоалгоритмы используют однонаправленные функции? 4. Как реализуется программное возведение в степень для больших чисел? БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Шаньгин В.Ф. Защита информации в компьютерных системах и сетях /В.Ф.Шаньгин. - М: ДМК, 2012.-593 с. 2. Введение в криптографию: новые математические дисциплины. Учебник/под ред. В.В.Ященко.- СПб: Питер, 2001.-287 с. 3. Иванов М.А. Криптографические методы защиты информации в компьютерных системах и сетях./ М.А. Иванов.- М.: Кудиц-образ, 2001.-363с. 4. Анин Б. Защита компьютерной информации./ Анин Б. - СПб,Киев,М.: БХВ-Петербург, 2000.- 368 с. 5. Брюс Шнайер. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си./ Брюс Шнайер- М:Триумф, 2002. – 816 с.
ЗАДАНИЕ № 1. ШИФРОВАНИЕ ДАННЫХ МЕТОДАМИ ПОДСТАНОВКИ, ПЕРЕСТАНОВКИ И ПОЛИАЛФАВИТНЫМИ ШИФРАМИ Цель работы: Приобретение навыков шифрования информации с использованием простейших методов шифрования.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 1127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.26.154 (0.01 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

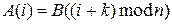 , (1.1)
, (1.1) 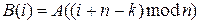 (1.2)
(1.2)