Заглавная страница
Избранные статьи
Случайная статья
Познавательные статьи
Новые добавления
Обратная связь

ТОП 10 на сайте

Приготовление дезинфицирующих растворов различной концентрации

Техника нижней прямой подачи мяча.

Франко-прусская война (причины и последствия)

Организация работы процедурного кабинета

Смысловое и механическое запоминание, их место и роль в усвоении знаний

Коммуникативные барьеры и пути их преодоления

Обработка изделий медицинского назначения многократного применения

Образцы текста публицистического стиля

Четыре типа изменения баланса

Задачи с ответами для Всероссийской олимпиады по праву

Мы поможем в написании ваших работ!

ЗНАЕТЕ ЛИ ВЫ?

Влияние общества на человека

Приготовление дезинфицирующих растворов различной концентрации

Практические работы по географии для 6 класса

Организация работы процедурного кабинета

Изменения в неживой природе осенью

Уборка процедурного кабинета

Сольфеджио. Все правила по сольфеджио

Балочные системы. Определение реакций опор и моментов защемления

Главная Избранные Случайная статья Познавательные Новые добавления Обратная связь FAQ

Розподіл балів модульних контролів

Стр 1 из 3Следующая ⇒

Функціональна електроніка

Та Електродинамічні процеси

Література:

1. Андрущак А., Готра З., Кушнір О. Прикладна електродинаміка інформаційних систем: Навчальний посібник / Львів: Видавничий центр НУ “Львівська політехніка”, 2012. – 324 с.

2. Хоружний В.А., Письмецький В.О. Функціональна мікроелектроніка, опто- та акустоелектроніка. – Харків, 1995, 186 с.

3. Сенько В.І., Панасенко М.В., Сенько Є.В. Електроніка і мікросхемотехніка. – Т.1. Елементна база електронних пристроїв. Київ, Обереги, 2000, 300 с.

4. Акаев А.А., Майоров С.А. Оптические методы обработки информации. М., 1988.

5. Носов Ю.Р. Оптоэлектроника. М., 1977.

6. Носов Ю.Р., Шилин В.А. Основы физики приборов с зарядовой связью. М., 1986.

7. Носов Ю.Р., Сидоров А.С. Оптроны и их применение. М., 1981.

Лабораторні заняття

№

П/п

Зміст /теми/ занять.

Годин и

ДФН

Бали

Ознайомлення з методами вимірювань та обладнанням для експериментів.

Дослідження поляризації електромагнітних хвиль НВЧ-діапазону. (Лаб. 2.1, стор. 173)

Дослідження ефективності екранування електромагнітних хвиль НВЧ-діапазону. (Лаб. 2.3, стор. 186)

Електромагнітні хвилі в прямокутних та циліндричних металевих хвилеводах. (Лаб. 2.4, стор. 195)

Поширення електромагнітних хвиль у діелектричних хвилеводах. (Лаб. 2.5, стор. 207)

Розподіл балів модульних контролів

Модульний контроль

Максимальна оцінка в балах

Поточний контроль

Контрольний захід (КЗ)

Модульна оцінка (ПК+КЗ)

Лабора -торні Прак -тичні РГР КР Разом балів (ПК) 1 2 3 4 5 6 7 8 4х5 4х5 - - Всього: 20 20 - - 40 60 100

ФІЗИЧНІ ОСНОВИ ФУНКЦІОНАЛЬНОЇ МІКРОЕЛЕКТРОНІКИ

МЕТА ВИВЧЕННЯ ДИСЦИПЛІНИ

Головним завданням сучасної мікроелектроніки є мікромініатюризація електронної апаратури на основі комплексу конструкторських, технологічних і схемних методів з метою зменшення її об'єму, маси, вартості, підвищення надійності та екологічності. Розвиток її на своєму традиційному шляху досяг настільки високого рівня технологічної інтеграції, що подальше її збільшення наштовхується на ряд фізичних і технологічних обмежень.

Паралельно з інтегральною мікроелектронікою розвивається інший напрям мікроелектроніки, що грунтується не на схемній радіотехніці з використанням статичних неоднорідностей і технологічної інтеграції, а на фізичних принципах інтеграції динамічних неоднорідностей, що виникають у процесі експлуатації електронної системи,— функціональна мікроелектроніка.

Динамічні неоднорідності, на відміну від неоднорідностей статичних, створюються не в процесі виготовлення електронного пристрою, а під впливом зовнішніх фізичних факторів у процесі його експлуатації.

Динамічними неоднорідностями в твердому тілі можуть бути електричні й магнітні домени та електродинамічні процеси між ними, магнітні вихори в надпровідниках другого роду, хвилі деформації кристала, пакети зарядів у потенціальних ямах тощо.

Таким чином, функціональна мікроелектроніка — це напрям мікроелектроніки, що грунтується на фізиці твердого тіла, електродинамічних процесах в ньому та принципі фізичного моделювання при здійсненні прийому, переробки, збереження, передачі й відображення інформації.

Які ж завдання необхідно розв'язати для широкого розвитку функціональної мікроелектроніки?

1. Одержати досконалі бездефектні матеріали. Тверде тіло є середовищем, де створюються динамічні неоднорідності й розвиваються процеси, що реалізують передаточну функцію.

2. Розробити фізичні основи динамічних неоднорідностей— мінімально можливі розміри, кінетику, деградацію, вплив зовнішніх факторів, взаємодію динамічних неоднорідностей різної фізичної природи тощо.

3. Розробити методи вимірювання основних фізичних характеристик динамічних неоднорідностей.

4. Шукати й синтезувати нові матеріали, активні середовища, придатні для формування в них динамічних неоднорідностей.

СТРУКТУРНА СХЕМА ФУНКЦІОНАЛЬНОЇ МІКРОЕЛЕКТРОНІКИ

Рис. 1.1. Галузі сучасної мікроелектроніки

Рис. 1.2. Основні напрями розвитку функціональної мікроелектроніки

Скалярні і векторні поля

Кожен раз, коли кожній точці деякої площини або простору відповідає число, говорять, що задана функція точки, або що є скалярне поле: U (x,y). Якщо кожній точці деякої області відповідає деякий вектор – задано векторне поле. Позначають векторне поле точки як (М) або (х, у, z).

Лінії рівня скалярного поля або горизонталі – це лінії, де U (x,y) = сonst.

У просторовому випадку рівняння U (x,y,z) = сonst – рівняння поверхні скалярного поля.

Векторне поле зображують за допомогою ліній, які у кожній точці дотикаються до вектора, що характеризує поле. Для уявлення про величину поля ці лінії проводять так, щоб їх число на одиницю площі, яка розташована перпендикулярно до ліній, було пропорційним до величини вектора.

У тих місцях, де поле сильніше, лінії проводять частіше, а там, де воно слабше, – рідше. Лінії векторів, які є силовими характеристиками поля (наприклад, лінії векторів

) називають силовими лініями поля. Нижче наведені приклади зображення різного виду ліній рівня скалярного поля.

Приклад 1: Приклад 2:

- зліва

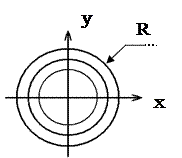
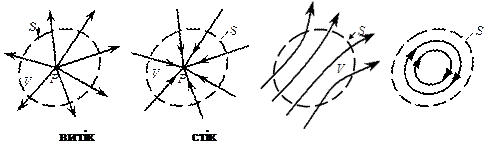
Лінії рівня у вигляді

Концентричних кіл

х² + y² = R² = const.

Або скалярне поле

U = x×y

Приклад 3.

Топографічний план:

Згущення: круті ділянки.

Додавання векторів

Додавання векторів зводиться до сумування їх компонентів:

; (1.5)

Для двохмірного варіанта (тобто, значення координати z рівне нулю) сума векторів знаходиться за правилом трикутника чи правилом паралелограма.

Скалярний добуток векторів

Скалярний добуток векторів 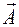і визначається таким чином:

(1.6)

де 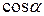– косинус кута між векторами і 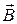. Звідси відома формула:

Властивості:

1. Якщо вектори ^, то ;

2. ;

3. ;

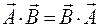4. ;

5. .

6. Якщо , тобто , то вектори 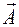і наз. ортогональними.

Подвійний векторний добуток

Він розкривається за формулою:

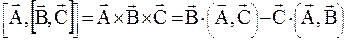. (1.9)

Тут скалярні добутки, що позначені за допомогою круглих дужок, входять як числа.

Градієнт

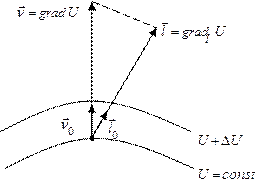
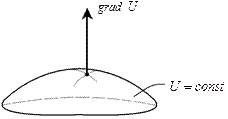
Нехай задано скалярне поле 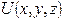. Введемо вектор 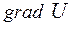, що називається градієнтом U, який направлений у сторону максимального збільшення U і рівний швидкості зміни U у цьому напрямку (див. рис. зліва).

Очевидно, що: 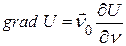, (1.10)

де 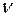– лінія, ортогональна до поверхні рівня. І: 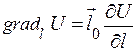. (1.11)

Тоді визначаючи проекції градієнта U в декартовій системі координат:

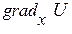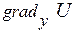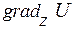, , , маємо: 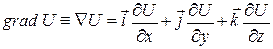. (1.12)

Скалярне поле U породжує векторне поле 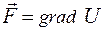. Таке векторне поле називається потенціальним, а скалярна функція – потенціалом. Поверхні рівня, на яких 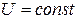, є еквіпотенціальними поверхнями. Тоді модуль градієнта рівний:

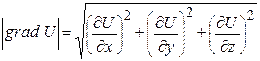Стрілка градієнта вказує на напрямок найбільшої крутизни (рис. зліва) Градієнт ще називають просторовою похідною (рис. зверху справа).

1.4. Силові лінії

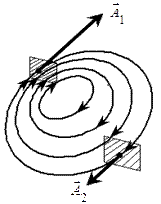
Для наглядного відображення векторний полів переважно будують картини так званих векторних, або силових ліній. Це лінії, дотичні до яких у кожній точці вказують напрямок вектора. Густина силових ліній може відповідати інтенсивності поля. При цьому кількість силових ліній, що проходять через ортогональну площадку, повинна бути пропорційна абсолютному значенню вектора, практично постійному в межах малої площадки (див. рис., де ).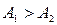

1.5. Потік вектора

Потік вектора через поверхню S (не обов’яз-ково замкнену) – це скалярна величина, яка чисельно рівна кількості ліній вектора, що пронизують дану площадку: 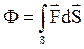, (1.13)

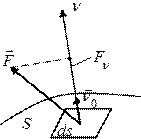де векторний диференціал 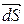розуміється як добуток звичайного (скалярного) диференціалу поверхні 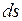на орт нормалі 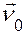, тобто 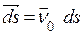. Тому 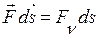. Якщо поверхня S замкнена, то 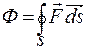, тоді 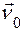– орт зовнішньої нормалі, який для незамкненої поверхні вибирається довільно. Потік Ф додатній, якщо силові лінії виходять з поверхні S назовні, і від’ємний, якщо вони входять всередину (тому що, кут між 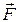і 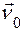у першому випадку гострий, а у другому – тупий). Потік вектора вимірюється числом його ліній, що виходять з поверхні, якщо густина ліній відповідає інтенсивності поля.

Є такі типи полів векторного поля 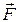в області V із поверхнею S:

Дивергенція

Потік вектора є інтегральною характеристикою поля, яка застосовується до кінцевого об’єму, але не дає інформації про розподіл зарядів в цьому об’ємі. У зв’язку з цим вводиться аналогічна диференціальна характеристика – дивергенція вектора, яка застосовується до точки. Зменшуючи поверхню, яка обмежує деякий об’єм простору до точки, отримаємо скалярну характеристику поля – дивергенцію.

Дивергенцією (а також розходженням) вектора 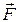називається величина, що визначається співвідношенням: 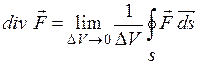. (1.14) Дивергенція – це скалярна функція координат. Позначаючи потік вектора 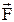через поверхню S як D Ф, можна написати:

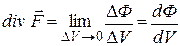або в декартових координатах: 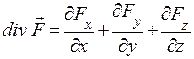(1.15)

Дивергенція – це диференціальна операція над компонентами вектора, що приводить до скалярної величини. Якщо в деякій точці 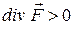, то ця точка є джерелом силових ліній – це є витік; якщо 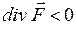, то точка є стоком. Якщо 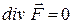, то лінії не починаються і не закінчуються в цій точці.

Циркуляція

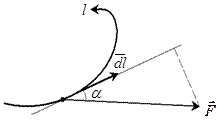Нехай задано довільне векторне поле 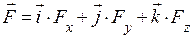і у цьому ж полі вибрана крива l, причому вказано додатній напрямок руху по ній (див. рис.). Лінійним інтегралом вектора 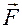по кривій l називається криволінійний інтеграл: 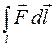. Враховуючи, що в декартових координатах диференціал дуги рівний 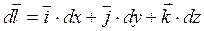, тоді будемо мати:

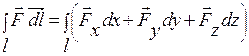
Якщо крива ℓ замкнута, то лінійний інтеграл вектора 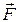вздовж неї так само називається циркуляцією вектора 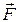вздовж ℓ:

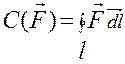. (1.16)

Ротор

Ротором (а також ротацією, вихором) вектора 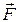називається векторна величина, що позначається символом 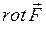. За визначенням, проекція 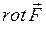на деякий напрямок 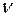(в точці, околом якої є площадка DS), є:

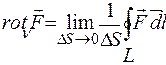. (1.17)

де 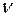– нормаль до площадки DS (орт 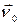); L– граничний контур D S, узгоджений з 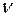правогвинтовою системою:

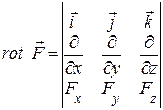
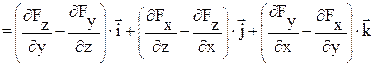. (1.18)

Ротор – це диференціальна операція над 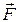, що приводить до нової векторної величини .

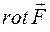Оператор Гамільтона

Англійський математик Вільям Гамільтон помітив, що основні диференційні операції, які проводяться над скалярними і векторними полями, можна дуже зручно записати, якщо ввести особливий символ: 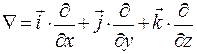. (1.19)

Цей символ отримав назву “ набла ” або “ оператор Гамільтона ”. (Слово “набла” по-грецьки означає “арфа”). Основні випадки застосування набла-вектора:

1. При множенні символічно Ñ на скалярну функцію U(x,y,z) отримуємо градієнт цієї ж функції: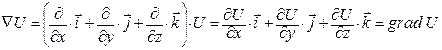

2. При множенні скалярно Ñ на векторну функцію F (x,y,z), отримуємо дивергенцію функції:

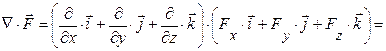
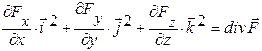
3. При множенні векторно набла-вектор Ñ на векторну функцію F (x,y,z), отримуємо ротор функції:

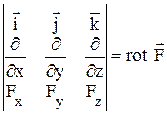
Диференціальний оператор діє тільки на той множник, який розташований безпосередньо за оператором. Приклади:

1. ;

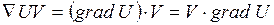2. ;

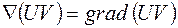3. ;

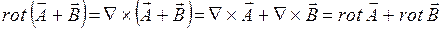4. 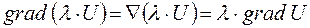, де 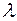– скаляр.

Приклади найпростіших полів

1. Трубчате (соленоїдальне) поле:

Поля, для яких 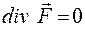, називають соленоїдальними. Оскільки , то поля є соленоїдальні.

2. Потенціальне (безвихрове) поле:

Це є поле, для якого . Раніше давали визначення потенціальному полю: Оскільки , тому потенціальні поля називають також безвихровими. Потенціальне поле 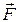характеризується інтенсивністю його витоків (стоків), тобто величиною як функцією координат.

Гармонічне поле

Потенціальні поля , для яких , можуть бути одночасно і соленоїдальними (), тоді вони називаються гармонічними.