
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Среднее арифметическое (выборочное среднее) ⇐ ПредыдущаяСтр 5 из 5
Среднее арифметическое (
где k — общее число вариантов, то формула вычисления среднего арифметического упрощается (повторяющиеся значения заменяются произведениями)
Если для признака построен интервальный ряд распределения, то среднее арифметическое вычисляется также как в случае дискретного ряда распределения, только вместо вариантов берутся середины интервалов. Показатели вариации Размах вариации. Лимиты Вариация — это изменчивость, рассеяние признака. Размах вариации (РВ) — это разность наибольшего и наименьшего значений признака в выборке, РВ = xmax – xmin. Лимиты (диапазон) — это значения xmax и xmin. Размах вариации показывает общую границу изменчивости признака. Показатель прост, но является слишком поверхностной оценкой, так как не дает представления об особенностях распределения значений внутри общих границ. Например, ряды наблюдений 1, 2, 4, 5, 7, 8, 10, 11 и 1, 5, 5, 6, 6, 7, 7, 11 имеют одни и те же лимиты (xmin = 1, xmax = 11), один и тот же размах вариации (РВ = 10), но значения признаков имеют совершенно отчетливые различия в расположении. В первом случае значения равномерно располагаются по области значений, во втором — концентрируются около значения признака, равного 6. Показатель вариации около центра Когда выбран показатель центра распределения, для оценки всей выборки удобно выбирать показатель вариации (изменчивости, рассеяния) отклонений значений признака от центра. Основным показателем центра распределения в математической статистике является среднее арифметическое. Если дан ряд наблюдений признака x 1, x 2,... xn, то достаточно найти среднее арифметическое (x 1 – Для оценки ряда отклонений от среднего арифметического в качестве показателей вариации рассматриваются: среднее линейное отклонение; дисперсия; стандартное отклонение. Если показателем центра распределения выбрана медиана, то для оценки вариации признака можно использовать квартильное отклонение.
Среднее линейное отклонение Среднее линейное отклонение (MD) — это среднее арифметическое абсолютных величин отклонений:
Формула достаточно проста и понятна, но на практике, как правило, не используется, так как плохо согласуется с теоретическими оценками теории вероятностей. Выборочная дисперсия Во избежании необходимости оценивать отклонения по абсолютной величине, используют оценку, которая носит название выборочной дисперсии или просто дисперсии (
В случае, когда признак является дискретным и для него составлен дискретный ряд распределения
формула для дисперсии получает вид
Если для признака составлен интервальный ряд распределения, то вместо вариантов берутся середины интервалов. Стандартное отклонение Выборочная дисперсия вычисляется как среднее квадратов отклонений. Возведение в квадрат несколько изменяет характер оценки вариации. Поэтому на практике чаще используют корень квадратный из дисперсии, т.е. стандартное отклонение Подставив выражение для выборочной дисперсии, получаем
Если построен вариационный ряд, то
где vi — варианты или середины интервалов, а mi — частоты. Стандартное отклонение называют также средним квадратическим или средним квадратичным отклонением. Стандартное отклонение имеет те же единицы измерения, что и основной признак. Стандартное отклонение позволяет с достаточной полнотой оценить характер отклонений признака от среднего арифметического. Если у двух рядов наблюдений одно и то же среднее арифметическое, то у ряда, в котором большие отклонения встречаются чаще, больше стандартное отклонение. Например, два ряда наблюдений имеют такие средние арифметические и стандартные отклонения: 1, 2, 4, 5, 7, 8, 10, 11;
1, 5, 5, 6, 6, 7, 7, 11; Лимиты, размахи и средние арифметические равны, но стандартное отклонение для первого ряда больше, т.к. большие отклонения встречаются чаще, чем во втором ряду.
Оценка формы распределения Асимметрия При оценке свойств измеряемого признака большое значение имеет симметрия частот отклонений относительно среднего арифметического. Она сказывается на форме полигона (гистограммы) распределения (форме распределения). Пусть по ряду наблюдений вычислены среднее арифметическое и ряд отклонений. Распределение частот симметрично, если отклонения со знаком "плюс" встречаются столько же раз, сколько такие же по абсолютной величине отклонения со знаком "минус". Симметрию легко выявить по полигону (ветви полигона симметричны относительно вершины) или по гистограмме. Для количественной оценки несимметричности распределения введен коэффициент асимметрии или просто асимметрия, который вычисляется по формуле
где s — стандартное отклонение. Если As = 0, распределение частот симметричное. Если As > 0, то чаще встречаются отклонения со знаком "плюс", и говорят о правосторонней асимметрии (полигон вытянут вправо относительно высшей точки). Если As < 0, то чаще встречаются отклонения со знаком "минус", и говорят о левосторонней асимметрии (полигон вытянут влево относительно высшей точки). На рис. 7 эти особенности схематично отображены. Рис. 7 Эксцесс Эксцесс (Ex) — это показатель, который описывает форму кривой распределения в смысле островершинности или плосковершинности. Обычно этот показатель применяют для описания унимодальных распределений частот. Вершина полигона острая, если небольшое число вариант около моды имеет превосходство в величине частоты (рис. 8). Если варианты в районе моды имеют примерно сравнимые частоты, то полигон будет плосковершинным (рис. 9). Значение эксцесса вычисляется по формуле
где s — стандартное отклонение. Если Ex = 0, распределение частот характеризуется как нормальное (встречается чаще всего). Если Es > 0, то распределение островершинное (рис. 8). Если Ex < 0, то распределение плосковершинное (рис. 9).
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2021-02-07; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.199.138 (0.009 с.) |
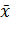 или M) является основной мерой центральной тенденции в математической статистике. Если x 1, x 2,... xn — первичный ряд наблюдений измеряемого признака в выборке объема n, то среднее арифметическое (выборочное среднее) вычисляется по известной формуле
или M) является основной мерой центральной тенденции в математической статистике. Если x 1, x 2,... xn — первичный ряд наблюдений измеряемого признака в выборке объема n, то среднее арифметическое (выборочное среднее) вычисляется по известной формуле  . Для сокращения записи сумму в числителе записывают с помощью знака суммы S (сигма большое). Тогда формула имеет вид
. Для сокращения записи сумму в числителе записывают с помощью знака суммы S (сигма большое). Тогда формула имеет вид 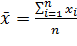 . Если признак является дискретным, и построен диcкретный ряд распределения вида
. Если признак является дискретным, и построен диcкретный ряд распределения вида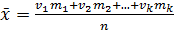 или
или 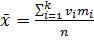 .
.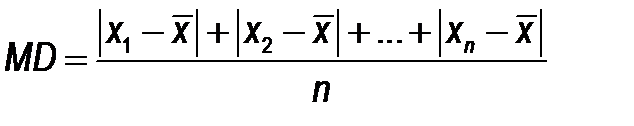 или
или 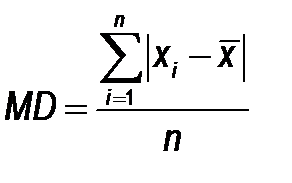 .
.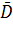 ). Для вычисления выборочной дисперсии в формуле для среднего отклонения абсолютные величины отклонений заменяют их квадратами, а в знаменателе вместо n записывают n –1 (это следствие из общей теории):
). Для вычисления выборочной дисперсии в формуле для среднего отклонения абсолютные величины отклонений заменяют их квадратами, а в знаменателе вместо n записывают n –1 (это следствие из общей теории):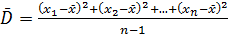 .
. , здесь k < n.
, здесь k < n.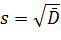 .
.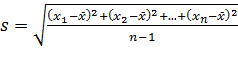 .
.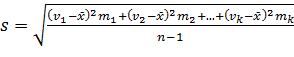 ,
,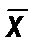 = 6; s = 3,625;
= 6; s = 3,625;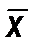 = 6; s = 2,777.
= 6; s = 2,777.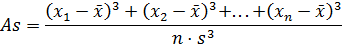
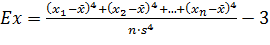 ,
,


