
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия электрического поля конденсатора.Содержание книги
Поиск на нашем сайте
Под энергией электрического поля конденсатора будем понимать энергию одной его обкладки, находящейся в поле, созданном другой обкладкой. Тогда: Формулы справедливы для любого конденсатора. Пример: С=2мкФ; U=1000В. t=10-6c. W=1 Дж
Плотность энергии.
Формула справедлива для полей любых конденсаторов и, кроме того, для полей, меняющихся со временем (неэлектростатических).
13. Деформа ́ ція (від лат. deformatio — «спотворення») — зміна розмірів і форми твердого тіла під дією зовнішніх сил(навантажень) або якихось інших впливів (наприклад, температури, електричних чи магнітних полів). При деформації точки твердого тіла змінюють своє положення. Точка із радіус-вектором
Деформа ́ ція (від лат. deformatio — «спотворення») — зміна розмірів і форми твердого тіла під дією зовнішніх сил(навантажень) або якихось інших впливів (наприклад, температури, електричних чи магнітних полів). При деформації точки твердого тіла змінюють своє положення. Точка із радіус-вектором Види деформацій[ред. • ред. код] Лінійна деформація[ред. • ред. код] Одновісний випадок[ред. • ред. код] Проявляється у розтягу-стисканні стержня вздовж його осі. Якщо вибрати у ненавантаженому стержні два перерізи, що розташовані на певній відстані і прикласти до нього зовнішні сили, то відстань між перерізами зміниться. Лінійна деформація ε у довільній точці тіла є границею відношення приросту довжини ΔL до початкової довжини L, коли сама довжина прямує до нуля.
Іншими словами при визначенні деформації в точці розглядаються зміни у її безпосередньому околі. Загальний випадок[ред. • ред. код] Для довільного тіла, що зазнає довільного деформування значення лінійних деформацій може відрізнятися у залежності від напрямку, у якому вони розглядаються. У цьому випадку лінійні деформації розглядаються в проекціях на осі декартових координат. Тоді деформація відрізка AB, що лежить на осі x і точка B яка після деформації переміститься у т. B' запишеться як:
Провівши подібний аналіз для осей y і z можна отримати відповідно εy i εz. Маючи дане поле переміщень
Деформація зсуву[ред. • ред. код] Аналогічно оцінюється деформація зсуву (зміна кутів) у безпосередньому околі точки. Кутова деформація γ є границею зміни кута між двома довільно обраними відрізками в тілі при прикладенні навантаження, коли довжини цих відрізків прямують до нуля. Маючи дане поле переміщень як і вище можна записати:
Об'ємна деформація[ред. • ред. код] Хоча деформації лінійні ε і кутові γ повністю описують деформований стан тіла, є інколи доцільним характеризувати інші види деформацій, як, наприклад, об'ємна деформація, що виступає як міра зміни об'єму тіла. З визначення об'ємна деформація то:
де: V(0) — початковий об'єм, V — кінцеве значення об'єму. Можна також довести, що в декартовій системі координат:
Тензорний запис деформації[ред. • ред. код] Використовуючи єдині позначення для обох типів деформації можна записати деформації у вигляді тензора деформації:
або у тензорному виді:
З порівняння тензорного запису з тардиційним для декартової системи координат можна отримати:
Об'ємна деформація: де: gij — контраваріантний метричний тензор. Типові види деформацій[ред. • ред. код] Найпоширеніші види деформації, котрі розглядаються опором матеріалів — згин, зсув (зріз), кручення, розтяг-стиск. Закон Гука Строга форма запису закону Гука[ред. • ред. код]
де Закон Гука був сформульований Робертом Гуком у 1660.
|
||||
|
Последнее изменение этой страницы: 2021-01-14; просмотров: 77; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.26.141 (0.005 с.) |

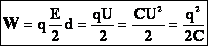
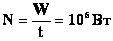 - опасно для жизни!
- опасно для жизни!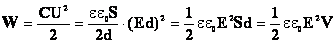
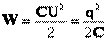
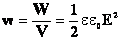 - плотность энергии (энергия единицы объема).
- плотность энергии (энергия единицы объема).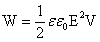
 при деформації має нове положення
при деформації має нове положення 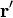 , тобто здійснить переміщення
, тобто здійснить переміщення 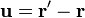 . Поле переміщень є однією з характеристик деформації, але воно незручне для математичного опису, оскільки, наприклад, при видовженні стрижня точки біля його початку зміщуються зовсім мало, а в кінці — доволі значно. Набагато важливіше те, наскільки точка тіла змістилася щодо сусідньої. Тому деформацію математично найзручніше описувати похідними від переміщення, які утворюють тензор, що отримав назву тензора деформації.
. Поле переміщень є однією з характеристик деформації, але воно незручне для математичного опису, оскільки, наприклад, при видовженні стрижня точки біля його початку зміщуються зовсім мало, а в кінці — доволі значно. Набагато важливіше те, наскільки точка тіла змістилася щодо сусідньої. Тому деформацію математично найзручніше описувати похідними від переміщення, які утворюють тензор, що отримав назву тензора деформації.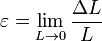
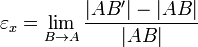
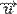 (компоненти вектора переміщень для усіх точок тіла) можна записати у загальному лінійні деформації як:
(компоненти вектора переміщень для усіх точок тіла) можна записати у загальному лінійні деформації як: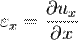 ;
; 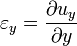 ;
; 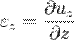
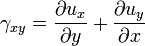 ;
; 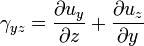 ;
; 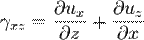
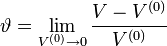
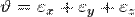
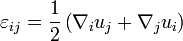 ,
,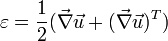

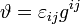 ,
,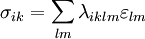 ,
,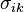 — тензор механічних напружень,
— тензор механічних напружень, 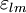 — тензор деформації, а
— тензор деформації, а 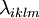 — тензор чертвертого рангу, який називається тензором модулів пружності і є характеристикою речовини.
— тензор чертвертого рангу, який називається тензором модулів пружності і є характеристикою речовини.


