Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Техническая результативность производства в длинном периодеСодержание книги
Поиск на нашем сайте
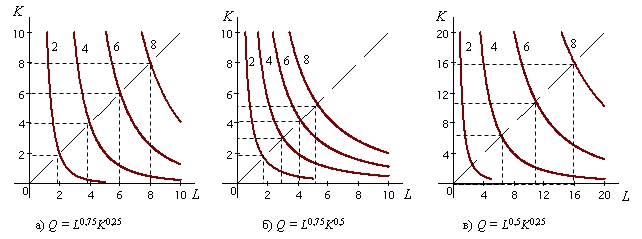
Так как в длинном периоде меняется не только количество используемого в производстве труда, но и объем капитала, то производственную функцию в нем можно представить в виде множества производственных функций в коротком периоде, различающихся объемами капитала. Шесть таких функций приведены в табл. 2.2. В столбцах показано изменение выпуска по мере увеличения труда при фиксированных объемах капитала, а в строках - при росте капитала и неизменных объемах труда. В целом это есть табличная форма представления производственной функции в длинном периоде. Типичной формой производственной функции в длинном периоде является степенная функция вида:
где А, Широкое применение в экономическом анализе получила функция Кобба - Дугласа2 Показатели степеней
При попытке оценить результативность производства в длинном периоде путем деления общего выпуска продукции на количество используемых факторов возникает затруднение из-за того, что нельзя суммировать число рабочих с числом станков или гектарами земли. Тем не менее определенную характеристику технологии можно получить, наблюдая за изменением выпуска при изменении объемов обоих факторов производства в одно и то же число раз, т.е. меняя масштаб производства. Результат воздействия на выпуск пропорционального изменения обоих факторов называют эффектом масштаба (returns to scale)3. Рост объемов труда и капитала в n раз может сопровождаться увеличением выпуска: 1) в n раз; 2) более, чем в n раз; 3) менее, чем в n раз. В первом случае говорят, что технология имеет неизменный эффект масштаба, во втором - растущий и в третьем - снижающийся. В табл. 2.3 приведены числовые примеры для каждого из них. Поскольку показатели степеней в производственной функции Q = AL
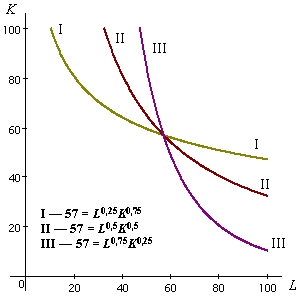
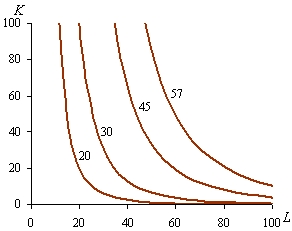
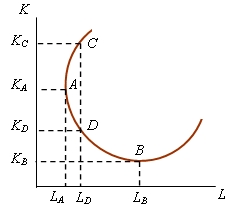
Изокванта является одним из основных инструментов графического анализа технической результативности производства. Поэтому выясним, чем определяются её конфигурация и расположение в пространстве K, L.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 89; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.15.34 (0.011 с.) |

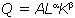 ,
, ,
, 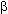 - положительные постоянные числа, характеризующие технологию производства.
- положительные постоянные числа, характеризующие технологию производства.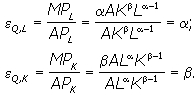
 Q,L =
Q,L =