
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Параллельность прямых и плоскостейСтр 1 из 5Следующая ⇒
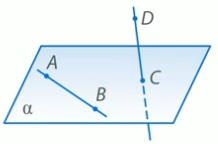
Тема: Параллельность прямых и плоскостей Урок: Скрещивающиеся прямые. Проведение через одну из скрещивающихся прямых Плоскости, параллельной другой прямой Тема урока На этом уроке мы рассмотрим определение скрещивающихся прямых и докажем теорему – признак скрещивающихся прямых. Определение скрещивающихся прямых Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Теорема 1 (признак скрещивающихся прямых) и ее доказательство Теорема (признак скрещивающихся прямых) Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся. Доказательство Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.
Рис. 1. Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость - α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана. Возможные случаи расположения прямых Три случая расположения прямых 1) Прямые a и b пересекаются в некоторой точке С:
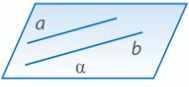
Рис. 2. 2) Прямые a и b параллельны: a ||b (Рис. 3.). Если прямые параллельны, то они лежат в одной плоскости и не пересекаются.
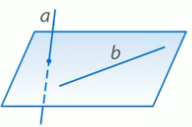
Рис. 3. Заметим, что и в первом, и во втором случае прямые лежали в одной плоскости. 3) Прямые a и b скрещиваются (Рис. 4.). То есть прямые a и b не лежат в одной плоскости.
Рис. 4. Пример скрещивающихся прямых в треугольной пирамиде Пример Дана треугольная пирамида ABCD, АВС – плоскость основания, точка D не лежит в плоскости АВС (Рис. 5.). Почему прямые АВ и DC скрещивающиеся?
Рис. 5. Прямая DC пересекает плоскость АВС в точке С, не лежащей на прямой АВ, а прямая АВ лежит в плоскости АВС. Значит, по признаку, прямые АВ и DC – скрещивающиеся. То есть противоположные ребра треугольной пирамиды лежат на скрещивающихся прямых.
Задача 1 Точка D не лежит в плоскости треугольника АВС, точки M,N,P – середины отрезков DA,DB и DC соответственно, точка K лежит на отрезке BN (Рис. 7.). Выясните взаимное расположение прямых.
Рис. 7.
1) ND и AB. Прямая ND - это другое обозначение прямой ВD. Прямая ВD и прямая АВ лежат в плоскости АВD и пересекаются. 2) PK и ВС. Прямые PK и ВС лежат в одной плоскости. Значит, они либо параллельные, либо пересекаются. Проведем среднюю линию NP (N,P – середины отрезков DB и DC соответственно). По свойству средней линии, прямая NP параллельна прямой ВС. Через точку Р можно провести только одну прямую, параллельную прямой ВС, и это прямая NP. Значит, любая другая прямая, проходящая через точку Р, не параллельна прямой ВС. Значит, PK и ВС пересекаются. 3) MN и AB. В треугольнике ABD точки M и N – середины сторон АD и ВD. Значит, МN – средняя линия. По свойству средней линии, МN параллельна АВ. 4) МР и АС. В треугольнике ADС точки M и Р – середины сторон АD и СD. Значит, МР – средняя линия. По свойству средней линии, МР параллельна АС. 5) КN и АС. Прямая КN и прямая ВD – это одна и та же прямая. Прямая АС лежит в плоскости АВС, прямая ВD пересекает плоскость АВС в точке, не лежащей на прямой АС. Значит, по признаку, прямые ВD и АС – скрещивающиеся. То есть, прямые КN и АС- скрещивающиеся. 6) МD и ВС. Прямая МD и прямая АD – это одна и та же прямая. Прямая ВС лежит в плоскости АВС, прямая АD пересекает плоскость АВС в точке, не лежащей на прямой ВС. Значит, по признаку, прямые АD и ВС – скрещивающиеся. То есть, прямые МD и ВС – скрещивающиеся. Задача 2 Докажите, что если АВ и СD скрещиваются, то АD и ВС тоже скрещиваются. Доказательство Предположим, что прямые АD и ВС не скрещивающиеся, то есть лежат в одной плоскости. Значит, все точки А, В, С,D лежат в этой плоскости, значит прямые АВ и СD тоже лежат в этой плоскости. Но прямые АВ и СD скрещивающиеся по условию. Получили противоречие. Значит, прямые АD и ВС – скрещивающиеся. Итоги урока Итак, мы познакомились со скрещивающимися прямыми: дали определение, доказали признак скрещивающихся прямых. Также мы доказали теорему о том, что через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна. Теперь нам известны все случаи взаимного расположения прямых в пространстве: они могут пересекаться, быть параллельными, быть скрещивающимися.
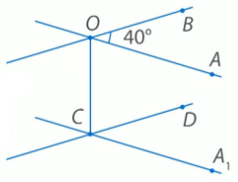
Задача 1 Прямые ОВ и СD параллельны, ОА и СD скрещиваются. Найдите угол между прямыми ОА и СD, если: 1) ∠ АОВ = 40°. Выберем точку С. Через нее проходи прямая СD. Проведем СА1 параллельно ОА (Рис. 7.). Тогда угол А1СD – угол между скрещивающимися прямыми ОА и СD. По теореме об углах с сонаправленными сторонами, угол А1СD равен углу АОВ, то есть 40°.
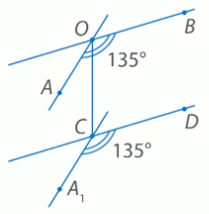
Рис. 7. 2) ∠ АОВ = 135°. Сделаем то же самое построение (Рис. 8.). Тогда угол между скрещивающимися прямыми ОА и СD равен 45°, так как он наименьший из углов, которые получаются при пересечении прямых СD и СА1.
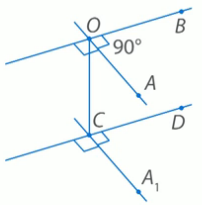
Рис. 8. 3) ∠ АОВ = 90°. Сделаем то же самое построение (Рис. 9.). Тогда все углы, которые получаются при пересечении прямых СD и СА1 равны 90°. Искомый угол равен 90°.
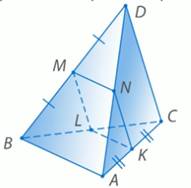
Рис. 9. Задача 2 1) Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.
Рис. 10. Доказательство Пусть нам дан пространственный четырехугольник ABCD. M,N,K,L – середины ребер BD,AD,AC,BC соответственно (Рис. 10.). Нужно доказать, что MNKL – параллелограмм. Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине. Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине. И МN, и LК параллельны АВ. Значит, МN параллельна LК по теореме о трех параллельных прямых. Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать. 2) Найдите угол между прямыми АВ и СD, если угол МNК = 135°. Как мы уже доказали, МN параллельна прямой АВ. NК – средняя линия треугольника АСD, по свойству, NК параллельна DС. Значит, через точку N проходят две прямые МN и NК, которые параллельны скрещивающимся прямым АВ и DС соответственно. Значит, угол между прямыми МN и NК является углом между скрещивающимися прямыми АВ и DС. Нам дан тупой угол МNК = 135°. Угол между прямыми МN и NК – наименьший из углов, полученных при пересечении этих прямых, то есть 45°. Итоги урока Итак, мы рассмотрели углы с сонаправленными сторонами и доказали их равенство. Рассмотрели углы между пересекающимися и скрещивающимися прямыми и решили несколько задач. На следующем уроке мы продолжим решение задач и повторение теории.
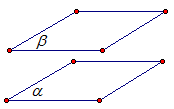
Тема урока На этом уроке мы дадим определение параллельных плоскостей и вспомним аксиому о пересечении двух плоскостей. Определения параллельных плоскостей Определение. Две плоскости называются параллельными, если они не пересекаются. Обозначение: Иллюстрация параллельных плоскостей (Рис. 1.)
Рис. 1. Аксиома А3 Существуют ли параллельные плоскости? Вспомним аксиому А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (Рис. 2.).
Рис. 2. То есть, еще остается случай, если две плоскости не имеют общей точки. Такие плоскости называются параллельными.
Задача 1 Плоскости Докажите, что прямая m параллельна плоскости Доказательство Предположим, что прямая m пересекается с плоскостью
Рис. 5. Задача 2 Докажите, что плоскости Доказательство Предположим, что плоскости
Рис. 6. Задача 3 Две стороны треугольника параллельны плоскости Доказательство Дан треугольник АВС и плоскость Через две пересекающиеся прямые АС и АВ проходит плоскость
Рис. 7. Итоги урока Итак, мы рассмотрели определение и признак параллельных плоскостей. На следующем уроке мы рассмотрим свойства параллельных плоскостей.
Тема урока Свойства параллельных плоскостей Свойство 1 Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Доказательство Пусть даны параллельные плоскости
Рис. 1. Прямые а и b лежат в одной плоскости, а именно в плоскости γ. Докажем, что прямые а и b не пересекаются.
Если бы прямые а и b пересекались, то есть имели бы общую точку, то эта общая точка принадлежала бы двум плоскостям и Итак, прямые а и b параллельны, что и требовалось доказать.
Свойство 2 Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
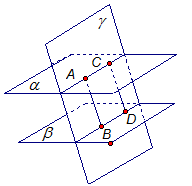
Рис. 2. Доказательство Пусть даны параллельные плоскости Две параллельные прямые АВ и СD образуют единственную плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости Прямые АВ и СD также параллельны (по условию). Значит, четырехугольник АВDС – параллелограмм, так как его противоположные стороны попарно параллельны. Из свойств параллелограмма следует, что отрезки АВ и СD равны, что и требовалось доказать. Свойство 3 Параллельные плоскости рассекают стороны угла на пропорциональные части. Доказательство Пусть нам даны параллельные плоскости
Рис. 3. Параллельные плоскости Значит, треугольники АВС и АВ1С1 подобны. Получаем:
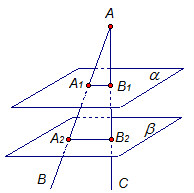
Свойство доказано. Решение задач Задача 1. Параллельные плоскости Найдите: а) АА2 и АВ2, если А1А2 =2 А1А =12 см, АВ1 =5 см. б) А2В2 и АА2, если А1В1 =18 см. АА1 =24 см,
Рис. 4. Решение: а) Пусть А1А = k, тогда по условию длина А1А2 =2 k =12 см., следовательно, k =6 см. Тогда отрезок АА2 =3 k =3∙6=18, т.е. АА2 =18 см. Две параллельные плоскости
Ответ: АА2 = 18 см, АВ2 = 15 см. б) Пусть А1А2 = k, тогда длина отрезка
Значит, Из подобия треугольников АА2В2 и АА1В1 следует, что
Ответ: А2В2 = 54 см, АА2 = 72 см. Итоги урока Итак, мы рассмотрели свойства параллельных плоскостей и использовали при решении некоторых задач. На следующем уроке мы рассмотрим тетраэдр.
Тема: Параллельность прямых и плоскостей
|
||||||||
|
Последнее изменение этой страницы: 2021-01-08; просмотров: 212; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.26.246 (0.068 с.) |
 (Рис. 2.). Как мы знаем, через две пересекающиеся прямые проходит единственная плоскость.
(Рис. 2.). Как мы знаем, через две пересекающиеся прямые проходит единственная плоскость.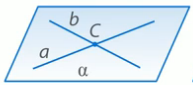


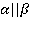 .
.

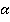 и
и 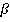 параллельны, прямая m лежит в плоскости
параллельны, прямая m лежит в плоскости 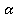 ). Но это невозможно, так как плоскости
). Но это невозможно, так как плоскости 
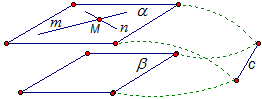
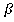 и притом только одна. Плоскость
и притом только одна. Плоскость 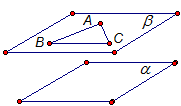
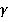 , которая пересекает плоскости
, которая пересекает плоскости 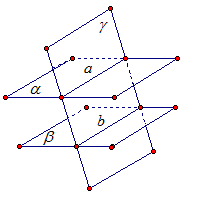
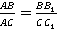 .
.
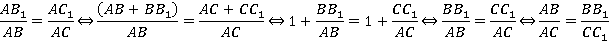
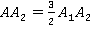 .
.
 см.
см.
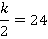

 см.
см.

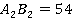 см.
см.


