Большие трудности вызывают у детей усвоение соотношения единиц времени и действия с этими величинами. Приведем фрагменты уроков.

I этап решения задачи — восприятие задачи

Вариант № 1 — иллюстрация (не является моделью, так как не отражает всю задачу, а только помогает представить сюжет задачи; наиболее уместна в тех случаях, когда дети совсем маленькие, речь идет о незнакомых объектах и когда дети — «образники»).

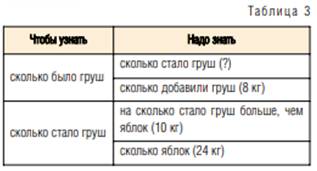
Вариант № 3 — перевод текста задачи на язык выражений с переменной (для алгебраического метода)

 х — было груш во второй корзине;

(х + 8) — стало груш во второй корзине;

(х + 8) – 10 — груш столько же, сколько яблок.

Так как известно, что яблок 24 кг, то можно составить уравнение.

II этап — поиск решения задачи

Вариант № 1 — по модели.

Искомый отрезок на чертеже (рис. 2) обозначен знаком «?». Видно, что он длиннее отрезка, изображающего количество яблок, которые были в корзине, на величину отрезка, который является разницей между отрезками, обозначающими 10 кг и 8 кг. Значит, надо сначала найти разность между 10 и 8, потом ее прибавить к 24, и найдем искомое число.

Вариант № 2 — рассуждения.

а) «От условия».

Рассуждения могут быть оформлены схемой (см. рис. 4) или таблицей (см. табл. 2).

Так как начали рассуждения от вопроса и пришли к данным, значит, рассуждения закончены.

Вариант № 3 — составить уравнение, которое является планом решения задачи.

а) Начало процесса составления уравнения рассмотрено нами на I этапе: так как яблок было 24 кг, а величина, выраженная в килограммах и равная этой, записана выражением (х + 8) – 10, то можно составить уравнение (х + 8) – 10 = 24;

б) пусть х — стало груш, тогда (x– 8) — было груш, (24 + 10) — стало груш. Так как одну и ту же величину записали разными выражениями, то можно составить уравнение х = 24 + 10. Так как надо узнать, сколько килограммов груш было найдено, то найдем х – 8.

III этап — выполнение плана решения задачи

Выполнение плана можно осуществить разными методами, т.е. воспользоваться для реализации намеченного плана средствами таких разделов математики, как арифметика, алгебра, геометрия, теория множества, логика. Кроме этого, выделен табличный метод решения задачи, где правильное заполнение таблицы позволит ответить на вопрос задачи. И наконец, можно использовать несколько средств, путей решения задачи, которые были описаны выше, тогда получается смешанный метод. Разные способы решения задачи.

Смешанный метод: смотрите на чертеж (см. рис. 4), выполненный в масштабе. Очевидно, что искомый отрезок длиннее отрезка, обозначающего количество яблок, на одну мерку, изображающую 2 кг. Выполняем единственное арифметическое действие, которым находим ответ на вопрос задачи: 24 + 2 = 26. Ответ: 26 кг груш было в корзине.

Геометрический метод. Делаем временную линейку с единичным отрезком, равным выбранному масштабу для нашего чертежа (см. рис. 3). Измеряем искомый отрезок. Получаем 26 ед. Переводим результат измерения в единицу той величины, о которой речь в задаче (кг), получаем ответ: 26 кг.

О т в е т: 26 кг груш было в корзине.

Алгебраический метод (решение уравнения)

1-й с п о с о б:                        2-й с п о с о б:

(х + 8) – 10 = 24                       х = 24 + 10

х + 8 = 24 + 10                              х = 34

х = 34 – 8                                 х – 8 = 34 – 8

 х = 26                                        х – 8 = 26

О т в е т: 26 кг груш было в корзине.

Арифметический метод (выполнение арифметических действий)

На I и II этапах были найдены 2 способа решения задач:

1-й способ:                                2-й способ:

 1) 24 + 10 = 34 (кг)                  1) 10 – 8 = 2 (кг)

2) 34 – 8 = 26 (кг)                      2) 24 + 2 = 26 (кг)

Форма записи для этих двух способов выбрана по действиям без пояснения, но возможно оформить арифметическое решение и по-другому.

На примере первого способа решения задачи рассмотрим остальные формы записи.

По действиям с пояснением.

1) 24 + 10 = 34 (кг) — стало груш.

2) 34 — 8 = 26 (кг) — было груш. О т в е т: 26 кг.

По действиям с вопросами.

1. Сколько килограммов груш стало?

24 + 10 = 34 (кг)

2. Сколько килограммов груш было?

34 – 8 = 26 (кг)

О т в е т: 26 кг.

Выражением: (24 + 10) – 8.

О т в е т: 26 кг груш было в корзине.

При записи ответа к задаче мы руководствуемся здравым смыслом.

Итак, на III этапе выполнение найденных планов осуществляется разными математическими средствами, т.е. задача решается разными методами. На II этапе мы смогли найти несколько разных планов решения задачи, т.е. найти несколько способов решения задачи в рамках одного и того же раздела математики, варьируя сочетания данных задачи. И наконец, задачу, решенную одним методом и одним способом, можно оформить по-разному.

IV этап — проверка решения

Если учесть, что на данный момент существуют две концептуальные точки зрения относительно сущности понятия величины: величина — это свойство и величина — это число, то какой точке зрения надо придерживаться? В некоторых учебниках математики и в учебниках физики величина — это свойство, а в учебниках геометрии под величиной понимают число.

Практика показывает, что при изложении и усвоении материала о величинах возникает ряд трудностей математического и методологического характера. Поэтому в этой статье мы опишем подход к понятию величины, основанный на трактовке древнегреческого философа Аристотеля (384–322 до н.э.), так как в основе его системы философии математики лежит понимание математических знаний как отражения объективного мира, что является методологической основой для многих математических понятий, в том числе для понятия величины.

Создавая систему философии математики, Аристотель писал: «Количеством называется то, что может быть разделено на составные части, каждая из которых является чем-то одним, данным налицо. То или другое количество есть множество, если его можно счесть, это — величина, если его можно измерить. Множеством при этом называется то, что делится на части не непрерывные, величиною — то, что делится на части непрерывные....Непрерывное есть само по себе нечто смежное. Смежное есть то, что, следуя за другим, касается его. Прерывное (дискретное) образование формируется соединением дискретных, далее не" делимых элементов. Но так как неделимое не имеет частей, им необходимо касаться целиком, но касающееся целиком не образует непрерывного» [2].

Исходя из философских рассуждений Аристотеля, величина предмета не может быть числом, так как его нельзя разделить на части непрерывные: число — абстрактное понятие. Следовательно, величина — это свойство предмета, оно определяет реальную сущность понятия величины. О том, что величина — свойство, говорит и тот факт, что величина является характеристикой объектов и явлений. А то, что характеризует объект или явление, называют свойством. Тогда по правилу силлогизма вели" чина предмета — это его свойство.

Свойство выражает характеристику предмета, которая обусловливает его различие или общность с другими предметами и обнаруживается в его отношении к ним. Каждый предмет обладает множеством свойств. К свойствам предметов относятся: масса, время, пол, цвет, запах, сообразительность, честность, форма, длина, площадь, знания, скорость, твердость, сила, температура и др.

Если рассматривать множества элементов различной природы, то можно заметить, что элементы каждого множества обладают какими-то общими свойствами хотя бы по" тому, что они входят в одно и то же множество: например, множество объектов, имеющих цвет, или множество объектов, имеющих длину. Общим свойством называют свойство, присущее всем предметам данного множества. Специфическое или индивидуальное проявление общего свойства в каждом элементе множества называют значением данного свойства. Ведь у каждого предмета того или иного множества, напри" мер, свой цвет или длина, т.е. значение цвета или длины.

Если значения цвета несут в себе качественную характеристику, порождая ответ на вопрос «Какой цвет?» (зеленый, красный, синий и т.д.), то значения длины кроме качественной характеристики (длинный — короткий) несут в себе количественную характеристику, порождая ответ на вопрос «Сколько?», и их можно записать определенным образом. Причем ответ на вопрос «Сколько?» наводит на размышление: «столько же», «много» или «мало», но по сравнению с чем?

Например, площадь, занимаемая посаженным картофелем на дачном участке, занимает «столько же» (относительно площади свеклы) места, что и площадь посажен" ной свеклы, «много» (относительно площади редиски) по сравнению с площадью посаженной редиски, но «мало» (относительно площади дачного участка) по сравнению с площадью всего дачного участка. Здесь речь идет о внешней определенности предмета, которая может выражаться количеством, если найдены критерии сравнения.

Длины предметов можно сравнивать приложением, массы — взвешиванием, емкость — вместимостью, время — продолжительностью события и т.д. Надо заметить, что сравнивают только однородные свойства предметов, т.е. такие, которые характеризуют одно реальное состояние предмета: или линейную протяженность, или инертность, или трехмерную протяженность, или продолжительность события и т.д.

Если, например, длина елочки занимает на прямой «столько же» места, что и длина волны, «много» места по сравнению с длиной стрелы, но «мало» места по сравнению с длиной палки, то значение длины елочки может выражаться количеством волн и записываться определенным образом — (|) волн; количеством стрел и записываться — (| | _|) стрел; количеством палок и записываться — (_|) палок. При этом длину волны, длину стрелы, длину палки называют единицами длины елочки.

Сравнение, которое «отвечает» на вопрос: «Равны ли длины елочки и волны?», устанавливает отношение равновеликости (елочка равна волне по длине). Отношение равновеликости рефлексивно, симметрично, транзитивно, т.е. является отношением эквивалентности, а следовательно, порождает разбиение множества предметов на классы эквивалентности равных по длине предметов.

Сравнение, которое «отвечает» на вопросы: «Во сколько раз длина елочки больше длины стрелы?» (в (| | _|) раза) и «Во сколько раз длина елочки меньше длины палки?» (в (_|) раза), устанавливает отношение кратности. Отношение кратности антисимметрично и транзитивно, т.е. является отношением нестрогого порядка.

Если задать вопрос: «На сколько длина елочки больше длины стрелы и меньше длины палки?», то ответ тоже будет выражаться количеством и запишется определенным образом: на (| _|) стрелы и на (|) елочку. Сравнение, которое «отвечает» на вопрос: «На сколько длина елочки больше длины стрелы и меньше длины палки?», устанавливает разностное отношение. Разностное отношение не подчиняется свойству транзитивности, но оно порождает отношение «больше» (или «меньше»), которое является отношением строгого линейного по" рядка.

Таким образом, длина елочки порождает ответы на вопросы: «Какова длина елочки по сравнению с длинами волны, стрелы и палки?» (равная, длинная или короткая), «Сколько волн, стрел и палок укладывается по длине елочки?» ((|) волна, (| | _|) стрелы и (_|) палки) и записывается определенным образом.

Свойства предметов: масса, время, длина, площадь, скорость, температура и др. — являются непрерывными, если любые смежные части предмета обладают той же величиной; их значения порождают ответы на вопросы «Какой?» (равный или относительно противоположный) и «Сколько?» (относительно конкретно); и их можно за" писать определенным образом. Такие свойства принято называть величинами.

Величина является обобщающим понятием непрерывных особых свойств предметов, является их абстракцией. Иначе говоря, величина — абстрактное понятие, выражающее качественно и количественно непрерывное свойство предмета. Качество определяется равенством (такой же) или относительной противоположностью (большой — маленький, тяжелый — легкий, высокий — низкий, толстый — тонкий, длинный — короткий и т.д.), количество определяется относительно выбранной единицы величины. Та" ким образом, абстрагирование от свойств предметов порождает понятие величины, реальная сущность которой определяется реальными свойствами предметов.

Если использовать формальную запись величины предметов: (|) волна, (| | _|) стрелы, (_|) палки и др., то мы переходим на второй уровень абстракции свойств предметов, который определяет формальную сущность понятия величины предметов (см. схему).

При постижении реальной и формальной сущностей понятия величины преодолевается разрыв между формальной записью (в том числе именованным числом) значения величины и реальным свойством пред" мета. Поэтому под величиной предмета с точки зрения реальности понимают свойство предмета, а с формальной точки зрения — формальную запись величины (именованное число). При таком подходе к понятию величины можно найти «точки соприкосновения» между всеми существующими трактовками понятия величины.

Определение: общее непрерывное свойство совокупности предметов, значения которого порождают ответы на вопросы «Какой?» (равный или относительно противоположный) и «Сколько?» (относительно конкретно) и их можно записать определенным образом, называется величиной.

Это определение величины построено конструктивно: через род и видовое отличие. Родовым понятием величины является «общее непрерывное свойство совокупности предметов», видовым отличием — «значения которого порождают ответы на вопросы «Какой?» (равный или относительно противоположный) и «Сколько?» (относительно конкретно) и их можно записать определенным образом».

Сформулированное определение можно использовать для распознавания величины предмета. Например:

— масса является общим непрерывным свойством совокупности предметов, и ее значения порождают ответы на вопросы: «Какая масса каждого из совокупности предметов такая же? тяжелее или легче? (равная или относительно противоположная)», «Сколько единиц содержится в массе каждого из совокупности предметов?» (относительно конкретно). Масса — величина;

— цвет тоже является общим непрерывным свойством совокупности предметов, но его значения порождают ответ только на вопрос: «Какой цвет каждого из совокупности предметов красный? голубой? зеленый? или другой?» (относительно не противоположный). Следовательно, цвет — не величина;

— синий цвет (синева) — общее непрерывное свойство совокупности предметов, и его значения порождают ответ на вопрос: «Какой синий цвет каждого из совокупности предметов такой же? Темный или светлый?» (равный или относительно противоположный). Но на вопрос: «Сколько единиц содержится в синем цвете каждого из совокупности предметов?» ответа нет, так как единица синего цвета не определена (не придумана). Синий цвет — не величина. Хотя если ввести единицу интенсивности си" него цвета и построить шкалу обозначений для каждого значения синевы (шкалу измерения), то синий цвет станет величиной.

Если А = {а, b, с, d, e,...} — множество предметов, обладающих величиной Ω, то отношение равновеликости порождает разбиение множество А на классы равных предметов по величине Ω: А = {А1, А2, А3, А4, А5,...}. Тогда отношения кратности или больше определят строгий линейный порядок между классами равных предметов по величине Ω. Множество А = {А1, А2, А3, А4, А5,...} станет упорядоченным по величине Ω, что позволяет построить шкалу обозначений для каждого значения вели" чины Ω (шкалу измерения).

Из вышесказанного можно сформулировать признаки определения величины предмета.

Величина предмета порождает ответ на вопрос «Какой?» (равный или относительно противоположный: большой — маленький, тяжелый — легкий, высокий — низкий, толстый — тонкий, длинный — короткий, сильный — слабый и т. д.) — качественная характеристика.

ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА

Цифра 0

— Сегодня мы познакомимся с цифрой 0. Это самая загадочная и необычная цифра, которой обозначают «отсутствие» чего-либо. Прибавьте 0 к 5 — получится 5. Ведь мы ничего к числу не прибавили — вот оно и осталось без изменения. Отнимите 0 от 6 — получится опять-таки 6. Сосчитайте, сколько в нашем классе сковородок. (Ни одной, значит, 0.)

Казалось бы, что о нем говорить: 0, он и есть 0 — пустышка. Недаром никчемного человека называют «ноль без палочки». Значит, подумает кто-то, ноль вовсе пустяковая цифра, без которой легко обойтись. Но это не так. Если разобраться, то выйдет, что 0 — очень даже важная «персона». Как, например, написать число 10, если нет 0? Долгие века люди не находили ответа на вопрос, как сделать так, чтобы запись цифр была простой и понятной. Так, в Индии за две тысячи лет до начала нашего летосчисления появился ноль. Его обозначили так же, как и сейчас. Но ведь мы уже привыкли к нему, а тогда это было великим открытием. Назывался он в то время просто кружком. А в древней Индии кружок — сунья. Арабы перевели это слово как цифр. Не правда ли, напоминает что-то?

Правильно! Цифр — цифра. Так уж получилось, что арабским именем нуля стали называть все остальные знаки. Все они теперь цифры: и 0 — цифра, и 5 — цифра, и 9 — цифра. А само слово ноль возникло позже от латинского nullum — ничто.

История линейки

— Знаете ли вы, что в 1989 году у линейки был юбилей. Ей исполнилось 200 лет. Однако линейкой пользовались и в более ранние времена. В Средневековье, например, немецкие монахи для разметки линий на листках пергамента (так называлась бумага) пользовались тонкими свинцовыми пластинками. А в ряде стран Европы, в том числе и в Древней Руси, для этих целей применялись железные прутья. Их называли шильцами. В разных странах люди измеряли одно и то же расстояние по-разному. Это было очень неудобно. Наконец, во Франции в 1789 году решено было ввести единую систему мер. В Париже изготовили платиновые линейки с делениями, которые стали образцами мерок для всего мира. По их образцу изготовили деревянные линейки. В Россию линейка попала после войны 1812 года в качестве военного трофея.

Числа 3 и 7

— Какую цифру вы любите больше всего? Семерку? А может, единицу? Вас удивляет такой вопрос: как можно любить или не любить какие-то цифры или числа? Однако не все так думают. У некоторых людей есть числа «хорошие» и «плохие». Например, числа 3 и 7 издревле считаются хорошими. Так уж сложилась их история. Сейчас мы можем легко сосчитать все карандаши в пенале, стулья на кухне. А в далекие времена человеку с трудом удавалось досчитать до двух. И каждый раз за двойкой начиналось что-то неизведанное, загадочное. Считали так: «один», «два», «много». Поэтому число 3, которое при счете должно было идти за числом 2, обозначало «все».

Долгое время у многих народов пределом счета была именно тройка. Так, число 3 стало излюбленным в мифах и сказках. Поэтому в сказках 3 медведя, 3 богатыря, 3 брата, 3 сестры и т.д.

Особым почетом в древности была окружена семерка. Отголоски почитания этого числа дошли до наших дней. Вспомните пословицы русского народа: «Семь бед — один ответ», «Семеро одного не ждут». Наша неделя состоит из семи дней. Древние заметили, что 7 нельзя поделить на равные части. Вот и назвали 7 — «не деля».

Умножение на пальцах

— Пальцевой счет был необходим в торговых местах, где сталкивались представители разных народов, не имевших общего языка. Знаки, изображаемые на пальцах, были понятны всем без слов. Этот прием умножения используется для чисел, которые больше 5, но меньше 10:

6 · 9 6 · 8 6 · 7 6 · 6 

7 · 9 7 · 8 7 · 7 7 · 6

8 · 9 8 · 8 8 · 7 8 · 6

9 · 9 9 · 8 9 · 7 9 · 6

Чтобы выполнить умножение на пальцах, нужно вытянуть на одной и другой руках столько пальцев, на сколько единиц каждый множитель превышает число 5. Сумма чисел вытянутых пальцев дает десятки произведения. Произведение чисел, соответствующее оставшимся не загнутым пальцам, дает единицы ответа. Полученные десятки и единицы нужно сложить. Это будет искомым произведением. Например, нужно было умножить 7 на 8. На одной руке показывали 3 пальца (8 > 5 на 3), на другой 2 (7 > 5 на 2). 3 + 2 = 5 — это десятки произведения чисел 7 · 8. На одной руке остались не загнутыми 2 пальца, на другой — 3. 2 · 3 = 6 — это единицы произведения: 7 и 8. Итак, 7 · 8 = 50 + 6 = 56.

Как люди научились измерять время

— Считать предметы мы умеем с первого класса. Это очень просто — один, два, три... Измерить расстояние тоже несложно. А как и чем измерять время? Самыми древними «часами», которые никогда не останавливались и не ломались, оказалось солнце. Утро, вечер, день — не очень-то точные мерки, но поначалу первобытному человеку этого было достаточно. Потом люди стали больше наблюдать за небом и обнаружили, что через определенное время на небосклоне появляется яркая звезда. Эти наблюдения сделали египтяне, и они же назвали эту звезду Сириус. Когда появлялся Сириус, в Египте отмечали наступление Нового года. Так появилась хорошо известная сейчас мера времени — год. Оказалось, что промежуток между появлением Сириуса состоит из 365 дней. Как видите, подсчеты древних египтян оказались достаточно точными. Ведь и наш год состоит из 365 дней. Но год слишком уж долгая мера времени. А для того чтобы вести хозяйство: посев, сбор, подготовку урожая, — нужны были более мелкие единицы времени, и люди вновь обратились к небу и звездам. На этот раз на помощь пришла луна, или по-другому — месяц. Все вы наблюдали за луной и знаете, что через определенное время она меняет свою форму: от тоненького серпа до яркого круглого диска (полнолуния). Промежуток между двумя полнолуниями и назвали месяцем. Оказалось, что месяц состоит примерно из 29 дней. Вот как точно в древнем мире умели определять время.

А семидневная неделя возникла в Вавилоне благодаря тем планетам, которые появлялись на небосклоне и были известны вавилонянам:

суббота — день Сатурна;

воскресенье — день Солнца;

понедельник — день Луны;

вторник — день Марса;

среда — день Меркурия;

четверг — день Юпитера;

пятница — день Венеры.

Если бы в Вавилоне были известны и другие планеты нашей Солнечной системы, возможно, наша неделя состояла бы не из 7, а из 9, 10 или 8 дней. Смена этих светил в течение месяца происходила примерно 4 раза. Вот и оказалось, что в месяце 4 недели.

Итак, самое сложное — найти мерки времени — было сделано уже в древнем мире. Этими мерами пользуются по сей день. Только вот называют их по(разному. На Руси название дней недели произошли от порядкового номера дня в неделе:

понедельник — по неделе, начинающей неделю;

вторник — второй день;

среда — середина недели;

четверг — четвертый день;

пятница — пятый день;

суббота, воскресенье — эти названия пришли из церковного словаря.

Выходит, что все главные меры времени (год, месяц, неделя) люди позаимствовали у природы еще много лет назад. Хотя этими мерками нельзя было измерить точное время, но главный шаг все-таки был сделан.

Из истории мер массы. Система мер у русского народа

— Сегодня мы узнаем, как люди научились определять массу различных предметов. Определите, что весит больше: карандаш или тетрадь? Теперь возьмите 8 карандашей в одну руку и тетрадь в другую. Что получилось? Значит, 1 тетрадь весит 8 карандашей. Вот мы и придумали новую единицу массы — «1 карандаш». Теперь в «карандашах» можно измерять все что угодно. Так поступали древние торговцы, используя различные подручные средства. Например, на Руси древнейшей мерой массы была гривна (или фунт) — кусок металла, масса которого по нынешним меркам равна примерно 410 граммам. Фунт делится на 96 золотников. Почему именно на 96, ведь гораздо проще было бы использовать круглое число? Оказывается, древние гири весили 1, 2, 3, 6, 12, 24, 48 золотников. Если все гири сложить вместе, то получится 1 + 2 + 3 + + 6 + 12 + 24 + 48 = 96 золотников. Так, 1 золотник весил примерно 4 грамма. Помните пословицу: «Мал золотник, да дорог»? Действительно, золотник весил очень мало.

В аптекарском деле применялась унция, которая равна примерно 30 граммам. Чтобы измерить более тяжелые предметы, использовался пуд, который равнялся 40 фунтам, или 16 кг, тонна (столько весила бочка с жидкостью), берковец (корзина, заполненная доверху).

История возникновения знаков плюс (+) и минус (–)

— Вы когда-нибудь задумывались над тем, откуда в наших тетрадях и учебниках появились такие необходимые и в то же время простые знаки «+» и «–»? Оказывается, их история уходит в глубокую древность. Обычно виноторговец черточками отмечал, сколько мер вина он уже продал. Так, уменьшение количества стало обозначаться знаком «–», который позже назвали минусом. Приливая в бочку новые запасы, торговец перечеркивал столько расходных черточек, сколько мер он восстановил. Так, возможно, появился знак «+», обозначающий прибавление, увеличение.

Иногда исторические факты со временем искажаются и не всегда бывают достоверными, поэтому многие ученые считают, что происхождение этих знаков имеет совсем другие корни. Давайте познакомимся и с другим мнением.

Раньше, когда знаки плюс и минус не были известны древним математикам, сумму чисел записывали так: 1 и 2 или на латинском 1 et 2. Для краткости стали писать 1 t 2, а потом 1 + 2.

История возникновения названий месяцев года

— Названия месяцев и их продолжительность ведут свое начало из Рима. Первым у римлян считался месяц, название которого произошло от имени бога войны Марса. Догадайтесь, что это за месяц? (Март). Рим славился своими мифами и легендами, поэтому многие вещи и предметы называли в честь вымышленных героев. Так, божество Янус дало название январю. Остальные месяцы стали называться от своих порядковых номеров. Были и такие месяцы, которые называли именами правителей государств: Юлий Цезарь (июль), император Август (август).

Но не только римляне были такими изобретательными. Многие старинные славяно-русские названия месяцев года существуют и по сей день в некоторых языках. В основном все они произошли от названия сельскохозяйственных работ или природных явлений каждого месяца:

январь — сечень (сечь, рубить дрова);

февраль — сухень или лютень (лютый, холодный ветер высушивал деревья);

март — березень (сожжение деревьев до золы для удобрения почвы);

апрель — квитень (цветение растений);

май — травень (появление травы);

июнь — червень (пробуждение насекомых);

июль — липень (цветение липы);

август — жнивень или серпень (пора жатвы);

сентябрь — вересень (вересеня — жатва);

октябрь — жовтень;

ноябрь — листопад;

декабрь — снежинь или грудень (груда — замерзший ком земли).

Из истории календаря

— Вы уже знаете, что календарь появил(ся много тысяч лет назад. Но каким он был? Похожим на современный или другим?

Сначала люди вообще не записывали чисел, а завязывали узелки на веревочках, представляя, что каждый узелок — это один день, или делали зарубки на деревянных брусках. Год в календарях древних начинался не зимой, как у нас, а летом. Отсчет вели от самого продолжительного дня в году, по нашему календарю это 21 июня. Календари были солнечные и лунные, в зависимости от того, за каким небесным телом велось наблюдение. Год по солнечным и лунным календарям начинался в разное время. Представляете, как было неудобно людям ориентироваться во временах года!

Но вот четыре тысячи лет назад в Англии создали первый письменный календарь. Он был высечен из камня. Само слово календарь произошло от латинского калере, обозначавшее выкликать, выкрикивать. Специальные служащие криками объявляли появление серпа луны в начале месяца. В то время у людей было множество приспособлений, которые мы можем назвать календарем. И все же наиболее удачным оказался египетский календарь, составленный по солнечному году. Египтяне установили, что в году 12 месяцев по 30 дней в каждом и еще 5 добавочных дней. Все трудности при создании календаря возникали по причине того, что ни месяц, ни год нельзя было разделить на целое число суток. И эти «лишние» доли, накапливаясь за годы, образовывали новые сутки. Чтобы решить эту проблему, император Юлий Цезарь приказал прибавлять эти новые сутки к каждому четвертому году, который называли високосным, т.е. 365 дней + 1 день. Но и эта мера оказалась недостаточной. Тогда римский папа Григорий III приказал с 4 октября сразу перейти к 15 октября, нагнав, таким образом, упущенные 10 суток. С этого момента начался новый стиль счисления времени, при котором високосными нельзя было считать года 1700, 1800, 1900, 2100, 2200, 2300 и т.д. Этот стиль назвали григорианским, в честь его учредителя Григория III, и распространили во многих государствах, в том числе и у нас. Летосчисление договорились вести условно от Рождества Христова, а новый год начинать с 1 января.

Миллион — 1 000 000;

1 000 миллионов = 1 миллиард, или биллион;

1 000 биллионов = 1 триллион;

1 000 триллионов = 1 квадраллион;

1 000 квадраллионов = 1 квинтиллион.

Измерение площади на Руси

— Мы часто говорили о практическом применении математических знаний в жизни человека. Необходимость заставила человека уже в древности измерять не только длину, расстояние, но и площадь предмета. В обычной жизни площадью мы называем большое, открытое пространство на улице, покрытое асфальтом. Но оказывается, что площадь можно найти и у крышки, и у тетради, и у учебника, и у пола в классе, и у земельного участка. Для измерения площади у русского народа были свои особые мерки: копна, выть, соха, обжа, коробья, веревка, жеребья. Но основными стали десяти и честь. Десятиной называлась поверхность квадрата со стороной 50 сажен (1 сажень = 2,1336 м). Хозяйственная десятина — поверхность прямоугольника со сторонами 40 и 80 сажен. Казенная десятина — поверхность прямо угольника со сторонами 30 и 80 сажен.

Сейчас мы не используем этих мер площади. От древних землемеров нам досталось только само слово площадь.

Из истории часов

— Хозяйственная деятельность человека требовала умения определять точное время. Сначала своеобразными часами было солнце. Так как Земля вращается вокруг своей оси, то кажется, что солнце движется по небосводу. Если вы наблюдательны, то наверняка замечали, что утром солнце «встает» с одной стороны горизонта, а «садится» на противоположной. В полдень же оно находится в самой высокой точке. А замечали ли вы, как при этом «движется» тень от предметов? Греки заметили это несколько тысяч лет тому назад и изобрели солнечные часы, которые достаточно точно показывали время, но были хороши только днем в ясную погоду.

Чтобы определять время ночью, люди использовали звездные часы. Ученые заметили, что все небесные тела кажутся движущимися из-за вращения Земли, и только одна-единственная яркая звезда остается неподвижной. Эта звезда называется Полярной. По положению созвездий относительно этой Полярной звезды и определялось ночное время.

Основная сложность в этих природных часах состояла в том, что по ним невозможно было засекать минуты и секунды. Так появились водяные и песочные часы, с помощью которых можно было измерять 1, 3, 5, 10... минут. До сих пор в языке сохранились такие выражения: «Ваше время истекло», «Время быстро течет». И только сравнительно недавно появились современные механические, а потом и электронные часы.

Название статьи: «Изучаем величины»

Автор: М. С. Матханова

Выходные данные: журнал «Начальная школа» выпуск №8 2004 г.

Электронный ресурс: https://n-shkola.ru/storage/archive/1408533174-323628675.pdf

 

При изучении тем «Единицы длины, массы» у некоторых учащихся вызывают затруднения упражнения вида: «Вырази в метрах: 17 км, 8 км 060 м и т.п., т.е. замена мелких единиц крупными и наоборот».

Я подготовила таблицу, с помощью которой ученики выполняют подобные задания без затруднений.

           В первой строке записаны единицы длины, начиная с наименьшей; во второй аналогично записаны единицы массы. Запись о p О (:) означает, что при переводе из мелких единиц в крупные мы будем выполнять деление. Например, надо 200 кг выразить в центнерах. На таблице видим, что килограмм (кг) расположен левее центнера (ц), значит, килограмм — более мелкая единица массы, чем центнер. Следовательно, надо выполнить деление: 1 ц = 100 кг, значит, 200: 100 = 2, следовательно, 2 ц = 200 кг.

Запись О p о (v) означает, что при переводе из крупных единиц в мелкие надо выполнять умножение. Например, надо узнать, сколько метров в 4 км. На таблице видно, что метр расположен левее километра, а при переводе из большей единицы измерения в меньшую производим умножение: 1 км = 1 000 м, 4 1 000 = 4 000, значит, 4 км = 4 000 м.

 Название статьи: «Проблемно-поисковые технологии при изучении геометрического материала»

Автор: Л. Д. Носенко

Выходные данные: журнал «Начальная школа» выпуск № 9 2004 г.

Электронный ресурс: https://n-shkola.ru/storage/archive/1407239479-1875461508.pdf

 

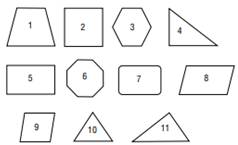
Тема: «Обобщение по теме «Единицы длины» (IV класс).

М 5 дм 45 м 4 м 50 см

Дм 4 дм 50 см

Сравни:

3 км 598 м … 35 080 м

16 дм … 1 м 60 см

5*. Реши задачу.

Чемпион по скорости роста среди растений — бамбук. Его стебель может вырасти за сутки на 40 см. На сколько увеличится высота бамбука за месяц, в котором 30 дней?

IV. Психологическая разгрузка. Задание на проверку глазомера. Двум парам учащихся предлагается показать названные величины, не используя при этом никаких измерительных инструментов.

Длина китайского крокодила — 2 м 50 см. Наиболее крупный крокодил (щучий аллигатор) в длину достигает 6 м 30 см.

Точность выполнения задания проверяется рулеткой.

V. Решение частных задач по применению имеющихся знаний.

1. Решение практической задачи: посчитать длину плинтуса класса.

— В процессе решения этой задачи мы нашли сумму длин сторон нашего класса. Как это назвать иначе? (Периметр.) Что такое периметр? Как еще можно вычислить периметр?

2. Работа с геометрическими фигурами. Учитель заранее чертит на доске следующие геометрические фигуры (см. рис. на с. 92).

— Назовите изображенные геометрические фигуры.

Выберите геометрическую фигуру (одну или несколько), периметр которой находится по формулам, где a, b, c — длины сторон многоугольников:

(a + b) * 2   (№ 5, 8, 2, 9)

a + b + c       (№ 4)

 a - 2 + b        (№ 11)

 a - n, где n — количество сторон многоугольника (№ 2, 3, 6, 9, 10)

a + b + c - 2 (№ 1) № 7 — «ловушка» (ни одна формула не подходит для вычисления периметра данной фигуры).

3. Практическая работа.

— Подберите числовые значения для сторон треугольника (фигура 4). Могут ли быть любые наборы чисел?

Из имеющихся у вас полосок сложите треугольник со сторонами 2 см, 6 см и 3 см.

После неудачных попыток проводится обсуждение. Самостоятельно или с помощью учителя четвероклассники делают вывод о том, что сумма двух сторон треугольника обязательно должна быть больше третьей стороны. Подобное задание выполняется и с другими фигурами.

VI. Рефлексия.

— Какие открытия для себя вы сделали сегодня? Какие знания, приобретенные на этом уроке, могут вам пригодиться в дальнейшем?

 

 

Название статьи: «К вопросу о формировании ключевых математических компетенций младших школьников»

Автор: А. В. Тихоненко

Выходные данные: журнал «Начальная школа» №4 2006 г.

Электронный ресурс: https://n-shkola.ru/storage/archive/1407237078-66353042.pdf