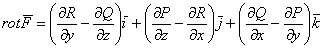Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление циркуляции векторного поля ⇐ ПредыдущаяСтр 2 из 2
1.Циркуляция (
Согласно общему принципу интегрирования, данный интеграл объёдиняет проекции «торчащих» из контура векторов – длины самого контура (чем длиннее, тем больше циркуляция); – скорости течения (чем длиннее векторы «эф», тем больше их бесконечно малые проекции и тем больше значение Если распишем криволинейный интеграл циркуляции для векторного поля
2. Вычисление по ф ормуле Стокса Циркуляция векторного поля
Нам следует вычислить поверхностный интеграл по верхней стороне треугольника. По сути, в правой части записан поверхностный интеграл 2-го рода – уже сведённый к поверхностному интегралу 1-го рода Найдём роторную функцию поля
Соленоидальное векторное поле Векторное поле a ¯(M) называется соленоидальным в области V, если во всех точках этой области diva ¯(M)=0 Согласно этому определению, поле не может иметь в области V источников и стоков, таким свойством обладает магнитное поле соленоида, что и объясняет происхождение термина. Соленоидально поле ротора любого достаточно гладкого поля: divrota ¯(M)=∇⋅[∇× a ¯]=0 Поток соленоидального векторного поля через поверхность σ, ограничивающую область Vσ ∈ V, равен нулю. Это прямое следствие формулы Остроградского.
СОДЕРЖАНИЕ
Теоретическая часть курсовой работы 1.1Тема 15. Криволинейные интегралы Тема 18. Гармонический анализ и элементы функционального анализа Тема 19. Операционное исчисление 1.3.1 Общие сведения о преобразовании Лапласа: оригинал и изображение Решение дифференциальных уравнений операторным методом Тема 20. Элементы теории поля 1.4.1 Вычисление производной функции в заданной точке по направлению заданного вектора и градиента функции
1.4.2 Вычисление поверхностного интеграла первого рода по поверхности S 1.4.3 Вычисление потока векторного поля через внешнюю поверхность пирамиды, образуемую плоскостью и координатными плоскостями 1.4.4 Вычисление циркуляции векторного поля 1.4.5 Соленоидальное векторное поле Практическая часть курсовой работы Список использованной литературы Список использованной литературы 1.Математический анализ /Векторное поле/, Е.Г.Пахомова, 2013 2.Справочное пособие по высшей математике. Т.2: Математический анализ: И.И. Ляшко, А.К. Боярчук, Я.Г. Гай, Г.П. Головач, 2015 3.Сайт mathprofi.ru 4. Математический анализ: Учебное пособие для студентов учреждений высшего профессионального образования / В.И. Гаврилов, Ю.Н. Макаров, В.Г. Чирский, 2017
Военный УЧЕБНО-НАУЧНЫЙ ЦЕНТР ВВС «Военно-воздушная академия им. профессора Н.Е. Жуковского и Ю.А. Гагарина»
___________________________________________
Курсовая работа по дисциплине: «Математический анализ» Вариант № 8
Исполнил: к-т Киселев А.А. уч.гр.21-95 воинское звание, фамилия и инициалы, номер учебной группы) Преподаватель: __________________ фамилия и инициалы
Воронеж – 2020
|
|||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 74; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.175.180 (0.008 с.) |
 ) векторного поля
) векторного поля 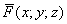 по контуру
по контуру 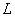 – это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру:
– это скалярная величина, численно равная криволинейному интегралу 2-го рода по этому контуру: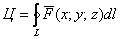
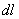 контура, что и является оценкой движения жидкости. И непосредственно из интеграла видно, что циркуляция зависит от двух вещей:
контура, что и является оценкой движения жидкости. И непосредственно из интеграла видно, что циркуляция зависит от двух вещей: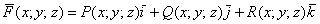 подробно, то перед нами «откроется» её физический смысл:
подробно, то перед нами «откроется» её физический смысл:
 , натянутую на данный контур в направлении, которое соответствует направлению обхода контура:
, натянутую на данный контур в направлении, которое соответствует направлению обхода контура:
 .
.