Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент силы относительно неподвижной точки и относительно неподвижной оси. Работа сил при вращательном движении. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси.Содержание книги
Поиск на нашем сайте
 
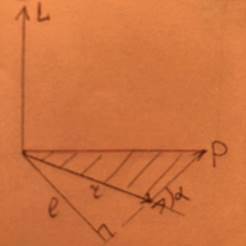
          Момент силы F относительно неподвижной точки О - физическая величина - векторное произведение радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F: M = [ rF ] M - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F Момент силы F относительно неподвижной точки О - физическая величина - векторное произведение радиуса-вектора r, проведенного из точки О в точку А приложения силы, на силу F: M = [ rF ] M - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F Модуль момента силы M = F r sinα = Fl, где α - угол между r и F, l - плечо силы.
Пусть сила F приложена в точке B, находящейся от оси вращения на расстоянии r, α - угол между направлением силы и радиусом-вектором r. Работа силы равна работе, затраченной на поворот тела. При повороте тела на бесконечно малый угол dφ точка B проходит путь ds = rdφ, и работа dA равна проекции силы на направление смещения на величину смещения:
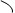  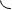 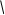            dA = dT - работа равна изменению кинетической энергии; dA = dT - работа равна изменению кинетической энергии;но dT = d 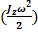 = Jzω dω, = Jzω dω,поэтому Mzdφ = Jzω dω, или Mz 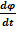 = Jzω = Jzω 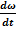 ; ;с учетом ω = 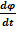 получим Mz = Jz получим Mz = Jz 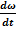 = Jzε - уравнение динамики вращательного движения. = Jzε - уравнение динамики вращательного движения.При совпадении оси вращения с главной осью инерции M = J 
Момент импульса материальной точки и твердого тела. Закон сохранения момента импульса. Момент импульса (количества движения) материальной точки А - физическая величина, определяемая векторным произведением L = [ rp ] = [ rmv ], Lz = В замкнутой системе M = 0,
Дифференциальное уравнение гармонических колебаний груза на пружине, математического и физического маятников, и его решение. Основные характеристики гармонических колебаний.
|
||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-17; просмотров: 144; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |


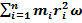 = ω
= ω 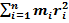 = Jzω
= Jzω 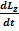 = Jz
= Jz  = M
= M