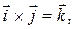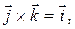Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами. Линейное пространствоСтр 1 из 2Следующая ⇒
Глава 2. ВЕКТОРНАЯ АЛГЕБРА
§1. Векторы, основные определения
Опр. Вектором называется направленный отрезок (отрезок, у которого различают начало и конец). Если А – начало, В – конец, то вектор обозначают
Часто вектор обозначают одной буквой
Опр. Длиной или модулем вектора Опр. Вектор, у которого начало и конец совпадают, называется нуль-вектором и обозначают Будем рассматривать только свободные векторы, т.е. те, которые можно переносить в любое место пространства, сохраняя длину и направление. Опр. Векторы
Опр. Векторы 1) имеют равные модули; 2) коллинеарны; 3) направлены в одну сторону.
Опр. Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.
Линейные операции над векторами. Линейное пространство I. Сложение векторов Правило треугольника
Правило параллелограмма
Отложить от т. О вектор
II. Вычитание векторов Опр. Разностью двух векторов Если Из определения вытекает правило построения
или
Итак:
III. Умножение вектора на число Опр. Произведением вектора 1) коллинеарный вектору 2) имеющий длину 3) тоже направление, что и
или
Операции сложения векторов и умножения вектора на число называются линейными. Они обладают свойствами: 1) 2) 3) 4) 5) 6) 7) 8)
Множество векторов пространства, удовлетворяющих свойствам 1–8, образуют линейное (векторное) пространство, которое обозначается R 3.
Проекция вектора на ось
Опр. Проекцией вектора
Свойства проекций 1. Проекция вектора
2. Проекция суммы векторов на ось равна сумме проекций слагаемых векторов на ту же ось.
3. При умножении вектора на число проекция на ось также умножается на это число.
4. Проекции двух равных векторов на одну и ту же ось равны.
III. Модуль вектора
По теореме о длине диагонали параллелепипеда
V. Направляющие косинусы
Направление вектора в пространстве определяется углами
По свойству 1 проекций:
или Тогда
I. Определение Опр. Скалярным произведением векторов
Придадим (3.5) другой вид (по свойству 1 проекций).
I. Определение Опр. Векторным произведением вектора 1) модуль вектора
2) вектор 3) направление вектора
Обозначается:
Глава 2. ВЕКТОРНАЯ АЛГЕБРА
§1. Векторы, основные определения
Опр. Вектором называется направленный отрезок (отрезок, у которого различают начало и конец). Если А – начало, В – конец, то вектор обозначают
Часто вектор обозначают одной буквой
Опр. Длиной или модулем вектора Опр. Вектор, у которого начало и конец совпадают, называется нуль-вектором и обозначают Будем рассматривать только свободные векторы, т.е. те, которые можно переносить в любое место пространства, сохраняя длину и направление. Опр. Векторы
Опр. Векторы 1) имеют равные модули; 2) коллинеарны; 3) направлены в одну сторону.
Опр. Векторы называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.
Линейные операции над векторами. Линейное пространство I. Сложение векторов Правило треугольника
Правило параллелограмма
Отложить от т. О вектор
II. Вычитание векторов Опр. Разностью двух векторов Если Из определения вытекает правило построения
или
Итак:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-09; просмотров: 80; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.193.158 (0.105 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (или
(или 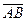 ).
).
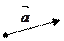
 .
.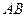 . Обозначают
. Обозначают  .
. .
. 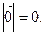
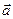 и
и 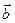 , расположенные на одной прямой или параллельных прямых, называются коллинеарными.
, расположенные на одной прямой или параллельных прямых, называются коллинеарными.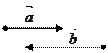

 и
и  называются равными, если они:
называются равными, если они: Опр. Вектор
Опр. Вектор  называется противоположным вектору
называется противоположным вектору 

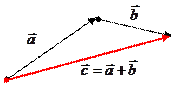 Суммой векторов
Суммой векторов  и
и  , который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов.
, который соединяет начало 1-го вектора с концом 2-го, при условии, что точка приложения 2-го вектора находится в конце 1-го. Распространяется на любое конечное число векторов. Частный случай. Сложение коллинеарных векторов.
Частный случай. Сложение коллинеарных векторов.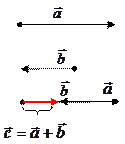

 . Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой
. Построить на этих векторах как на сторонах параллелограмм. Вектор, служащий диагональю параллелограмма, проведенный из т. О, является суммой  .
.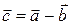 , который будучи сложенным с вектором
, который будучи сложенным с вектором  то
то  .
.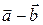 .
.
 направлен из конца вычитаемого к концу уменьшаемого.
направлен из конца вычитаемого к концу уменьшаемого.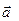

 Частный случай.
Частный случай.
 ;
; , противоположное направлению
, противоположное направлению 

 единичный вектор (орт) вектора
единичный вектор (орт) вектора 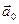 коллинеарен
коллинеарен 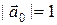 . Тогда
. Тогда (3.1)
(3.1) .
.


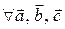
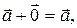

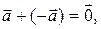


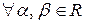

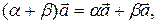
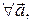
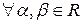
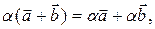
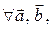

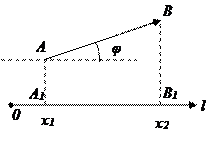 Пусть даны: l – некоторая ось и
Пусть даны: l – некоторая ось и 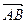 – произвольный вектор.
– произвольный вектор. проекция А на ось l,
проекция А на ось l,  координата
координата 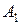 на l;
на l; проекция B на ось l,
проекция B на ось l, 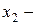 координата
координата  на l.
на l.
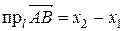 .
.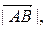 умноженному на косинус угла
умноженному на косинус угла  между
между 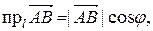 где
где 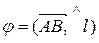 .
.
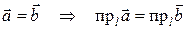 .
.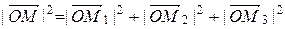 или
или 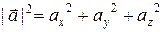 .
.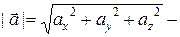 модуль вектора
модуль вектора 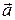 .
.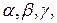 которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е.
которые вектор составляет с осями Ox, Oy, Oz. Косинусы этих углов, т.е. 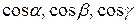 называются направляющими косинусами вектора.
называются направляющими косинусами вектора.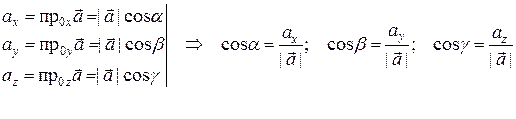

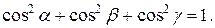
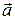 и
и 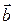 называется число, равное произведению модулей этих векторов на косинус угла между ними.
называется число, равное произведению модулей этих векторов на косинус угла между ними.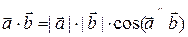 . (3.5)
. (3.5) проекция
проекция  на ось, определяемую
на ось, определяемую 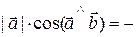 проекция
проекция 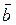 .
. (3.6)
(3.6)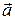 на вектор
на вектор 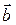 называется вектор
называется вектор  , который определяется следующим образом:
, который определяется следующим образом: численно равен площади параллелограмма, построенного на векторах
численно равен площади параллелограмма, построенного на векторах 
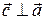 ,
, 
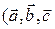 ориентированы как
ориентированы как  прав. тройка).
прав. тройка).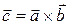 или
или 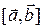 .
. Частные случаи:
Частные случаи: