
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование процессов с помощью уравнения парной линейной регрессии
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров. Параметризация модели осуществляется следующим образом. Линейная регрессия сводится к нахождению уравнения вида:
Уравнение вида Информационный этап заключается в формировании массива исходных (фактических, эмпирических, реальных) данных х i и у i. На этапе идентификации находят численные значения параметров
Т.е. из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.):
Рисунок 1.1 - Линия регрессии с минимальной дисперсией остатков.
После несложных преобразований, получим следующую систему линейных уравнений для оценки параметров
Решая систему уравнений (6), найдем искомые оценки параметров
где
Следует отметить, что в данных формулах используются фактические значения массивов данных х i и у i.
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях. Параметр На этапе верификации оценивают качество полученной модели и ее пригодность для прогноза. Для этого необходимо: - оценить тесноту связи между фактором и результатом; - оценить качество подбора линейной функции; - оценить значимость уравнения регрессии в целом; - оценить значимость отдельных параметров уравнения регрессии. Для оценки тесноты связи между фактором и результатом для линейной регрессии используют линейный коэффициент корреляции
Между коэффициентами b и если b > 0, то r > 0, если b < 0, то r < 0. Линейный коэффициент корреляции находится в пределах: Если - отсутствие связи между признаками; - наличие нелинейной формы связи. Интерпретация значений если | если r ≈ 0 → связи нет, или → связь нелинейная. Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции
где
Остаточная дисперсия результативного признака (не объясненная уравнением) находится по формуле (16):
Общая дисперсия результативного признака находится по формуле (17):
Соответственно величина После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценить значимость уравнения регрессии – это означает установить, соответствует ли математическая модель, выражающая зависимость между Y и Х, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y. Оценка значимости уравнения регрессии производится для того, чтобы узнать, пригодно уравнение регрессии для практического использования (например, для прогноза) или нет. При этом выдвигают основную гипотезу о незначимости уравнения в целом, которая формально сводится к гипотезе о равенстве нулю параметров регрессии, или, что то же самое, о равенстве нулю коэффициента детерминации: Оценка значимости уравнения регрессии в целом производится на основе Согласно основной идее дисперсионного анализа, общая сумма квадратов отклонений переменной где
Схема дисперсионного анализа имеет вид, представленный в таблице 1.2 ( Таблица 1.2 – Схема дисперсионного анализа
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину
Фактическое значение Для парной линейной регрессии Величина
Значимость отдельных параметров уравнения оценивается с помощью t -статистики по формулам:
где
Стандартная ошибка коэффициента регрессии
где Стандартная ошибка параметра
Стандартная ошибка параметра r xy определяется по формуле (27):
Для оценки существенности каждого параметра фактическое значение Существует связь между
Таким образом, проверка гипотез о значимости коэффициента регрессии и коэффициента корреляции проводится одинаково. Если коэффициент регрессии статистически значимый, то коэффициент корреляции тоже статистически значимый. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации: Средняя ошибка аппроксимации не должна превышать 8–10%. Для построения прогноза по уравнению регрессии необходимо подставить в уравнение Однако точечный прогноз очень ненадежен. Вероятность того, что реальное значение у совпадет с прогнозным
где Среднюю ошибку прогноза можно определить по формуле (30):
где
Стандартная ошибка
Таким образом, можно сделать вывод, что при х = х p, Пример расчета параметров парной линейной регрессии
В таблице 1.3 приведены данные о доле в расходах, направленной на потребление продуктов питания и заработной плате по нескольким регионам Уральского Федерального округа. Так как заработная плата характеризует одну из статей доходов домохозяйств, причем основную, а доля расходов на потребление продуктов питания – основную статью расходов, эти два показателя должны быть связаны между собой. Х – заработная плата; У – доля расходов на потребление продуктов питания, так как доля расходов зависит от заработной платы. Задание: 1) параметризация: подобрать уравнение связи; 2) идентификация: идентифицировать параметры уравнения, измерить тесноту связи между фактором и результатом; 3) верификация: оценить надежность модели, сделать выводы; 4) прогнозирование: - оценить уровень потребления при заданной заработной плате 58,0 млн.руб. - оценить уровень потребления при заданной заработной плате равной ( Порядок решения: 1) Параметризация: выберем для подбора параметров уравнение парной линейной регрессии, как получившее наибольшее распространение, наиболее легко идентифицируемое и интерпретируемое. Общий вид уравнения парной линейной регрессии в соответствии с формулой (4) следующий: у = а + bх + e 2) На этапе идентификации необходимо вместо буквенных обозначений параметров а и b найти числа, соответствующие данной парной регрессии. Найдем параметры а и b по формулам (7) и (8). Все предварительные расчеты приведены в таблице 3.
Таблица 1.3 – исходные данные для расчетов
Итого |
405,2 |
384,3 |
22162,3 |
21338,4 |
23685,8 |
210,3 |
0,646 |
230,47 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ср. знач. |
57,9 |
54,9 |
3166,0 |
3048,3 |
3383,7 |
30,05 |
0,092 |
32,924 |
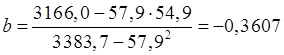
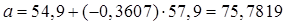
Также для определения параметров уравнения можно воспользоваться встроенной функцией категории «Статистические» → «ЛИНЕЙН». Подробнее об использовании этой функции см. Приложение 3.
Таким образом, по формуле (3) мы получили следующее уравнение парной линейной регрессии:
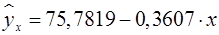
Вывод: при увеличении доходов на 1 млн. руб. потребление снижается на 360,7 тыс. руб.
|
|
Оценим тесноту связи между фактором и результатом с помощью линейного коэффициент корреляции 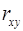 (14), (9), (17):
(14), (9), (17):
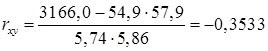
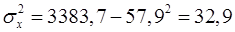

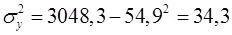
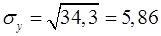
Вывод: связь обратная, слабая. При увеличении доходов потребление снижается с невысокой вероятностью.
3) На этапе верификации оценим качество модели. Для этого рассчитаем ошибку аппроксимации, коэффициент детерминации, F -критерий, t -статистику.
Рассчитаем ошибку аппроксимации по формуле (29) и столбцу 10 таблицы 3:
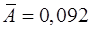 , или 9,2%.
, или 9,2%.
Вывод: Ошибка аппроксимации на превышает 8-10%, модель довольно точно описывает данные.
Рассчитаем коэффициент детерминации по формуле (15), (16) и (17) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:
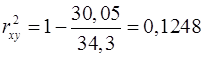
Вывод: уравнение объясняет всего 12,5% вариации результата
Рассчитаем F -критерий по формулам (19) и (21) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:

Определим F табл по таблице Приложения 1. Степени свободы числителя и знаменателя определим по таблице 2 (стр10). Число наблюдений – 7, параметр при х один – это b. Таким образом, k 1 = 1, k 2 = 5.
F табл = 6,61
Вывод: F факт < F табл следовательно гипотезу о статистической незначимости уравнения связи нужно принять. Уравнение связи статистически незначимо, то есть значения параметров могли быть получены случайным образом.
Рассчитаем t -статистику для каждого параметра по формулам (22)-(28) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:
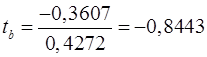
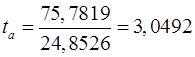
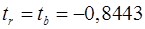
Определим t табл для 5 степеней свободы и вероятности 0,95 по таблице Приложения 3. При поиске табличного значения учтем, что t-критерий симметричен относительно оси х, поэтому сравниваем значения фактические и табличные по модулю.
t табл = 2,4669
Вывод: 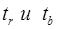 меньше t табл следовательно с вероятностью 95% параметры r и b признаются статистически незначимыми.
меньше t табл следовательно с вероятностью 95% параметры r и b признаются статистически незначимыми.
В свою очередь,  больше t табл следовательно с вероятностью 95% параметр а признается статистически значимым.
больше t табл следовательно с вероятностью 95% параметр а признается статистически значимым.
4) прогнозирование: оценим уровень потребления при заданной заработной плате 58,0 млн. руб. на доверительном интервале с заданной вероятностью по формулам (30) и (31).
Для нахождения 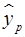 подставим в уравнение связи заданное значение х:
подставим в уравнение связи заданное значение х:
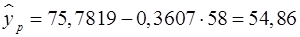 млн. руб.
млн. руб.
Вывод: при уровне заработной платы на уровне 58 млн. руб. потребление составит 54,86 млн. руб. Однако точечный прогноз явно не реален, вероятность того, что реальное значение у совпадет с прогнозным 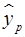 , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал.
, очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал.
Стандартную ошибку прогноза  определим по формуле (32) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:
определим по формуле (32) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:
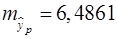
Тогда среднюю ошибку прогноза определим по формуле (30). Для этого самостоятельно зададим требуемый уровень надежности (90%, 95% или 99%) и по таблице Приложения 3 для 5 = 7 - 2 степеней свободы определим t табл. Пусть уровень надежности равен 90%, тогда t табл = 2,0150.
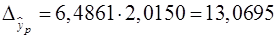 млн. руб.
млн. руб.
Тогда границы доверительного интервала составят:
(54,86-13,07) млн. руб. < 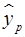 < (54,86+13,07) млн. руб.
< (54,86+13,07) млн. руб.
или 41,79 млн. руб. < 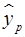 < 67,93 млн. руб.
< 67,93 млн. руб.
Вывод: с вероятностью 90% при заработной плате на уровне 58 млн. руб. потребление составит [41,79; 67,93].
Далее оценим уровень потребления при заданной заработной плате равной (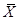 +5%).
+5%).
Для этого сначала рассчитаем уровень заработной платы, для которого нужно построить прогноз. Средняя заработная плата по данным таблицы 3 составляет 57,9 млн. руб. Найдем уровень заработной платы (Xi) для построения прогноза как:
57,9 х (1 + 0,05) = 60,8 млн. руб.
5) Далее проведем все действия аналогично предыдущему прогнозу. Сначала оценим уровень потребления при заданной заработной плате 60,8 млн. руб. на интервале с заданной вероятностью по формулам (30) и (31).
Для нахождения 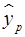 подставим в уравнение связи заданное значение Xi:
подставим в уравнение связи заданное значение Xi:
 млн. руб.
млн. руб.
Вывод: при уровне заработной платы на уровне Xi = ( +5%) млн. руб. потребление составит 53,86 млн. руб. Однако точечный прогноз явно не реален, вероятность того, что реальное значение у совпадет с прогнозным
+5%) млн. руб. потребление составит 53,86 млн. руб. Однако точечный прогноз явно не реален, вероятность того, что реальное значение у совпадет с прогнозным 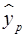 , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал прогноза.
, очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал прогноза.
Стандартная ошибку прогноза 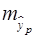 зависит от уравнения связи, поэтому для всех прогнозов по данному уравнению она постоянна. Поэтому, если не менять уровень надежности, то и средняя ошибка не изменится. Поэтому можно сразу построить прогноз:
зависит от уравнения связи, поэтому для всех прогнозов по данному уравнению она постоянна. Поэтому, если не менять уровень надежности, то и средняя ошибка не изменится. Поэтому можно сразу построить прогноз:
(53,86-13,07) млн. руб. < 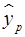 < (53,86+13,07) млн. руб.
< (53,86+13,07) млн. руб.
или 40,79 млн. руб. < 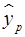 < 66,93 млн. руб.
< 66,93 млн. руб.
Вывод: с вероятностью 90% при заработной плате на уровне (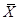 +5%) млн. руб. потребление составит [40,79; 66,93].
+5%) млн. руб. потребление составит [40,79; 66,93].
С помощью мастера диаграмм нанесем на график исходные данные и линии, характеризующие взаимосвязь, см. пример на рисунке 2.
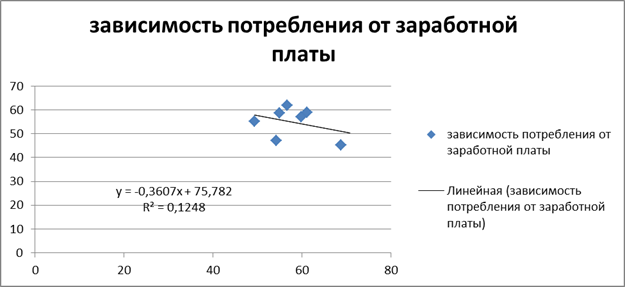
Рисунок 1.2 – Зависимость потребления от заработной платы
Для того, чтобы нанести на диаграмму уравнение связи и оценку аппроксимации (R2) воспользуемся функцией «Дополнительные параметры линии тренда» меню «Диаграмма», как на рисунке 3.
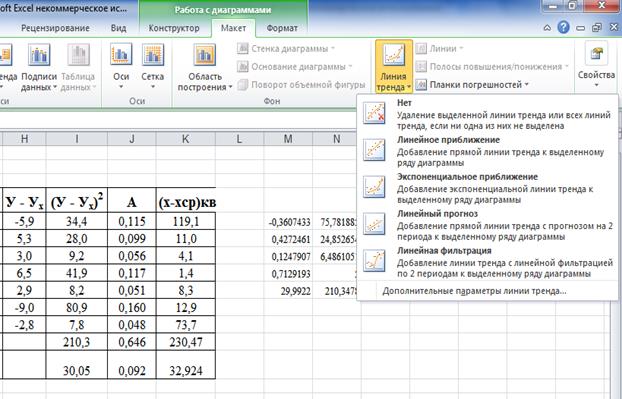
Рисунок 1.3 – Работа с диаграммой MS Excel
 (3)
(3)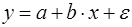 (4)
(4) находить теоретические значения результативного признака, подставляя в него фактические значения фактора
находить теоретические значения результативного признака, подставляя в него фактические значения фактора 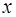 .
.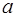 и
и  . Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров
. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров 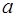 и
и 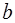 , при которых сумма квадратов отклонений фактических значений результативного признака
, при которых сумма квадратов отклонений фактических значений результативного признака 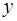 от теоретических
от теоретических  минимальна:
минимальна: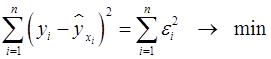 . (5)
. (5)
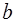 :
: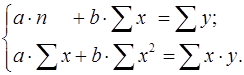 (6)
(6)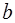 . Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (6):
. Можно воспользоваться следующими готовыми формулами, которые следуют непосредственно из решения системы (6): , (7)
, (7)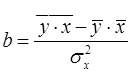 , (8)
, (8)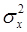 – дисперсия признака
– дисперсия признака 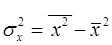 , (9)
, (9)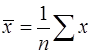 , (10)
, (10)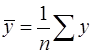 , (11)
, (11)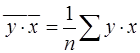 , (12)
, (12)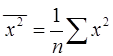 (13)
(13) , который можно рассчитать по следующим формулам:
, который можно рассчитать по следующим формулам: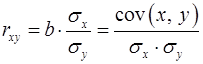 , (14)
, (14) существует следующая зависимость:
существует следующая зависимость: . Чем ближе абсолютное значение
. Чем ближе абсолютное значение  имеем строгую функциональную зависимость).
имеем строгую функциональную зависимость).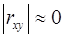 , то это может означать:
, то это может означать: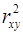 , называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака
, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака 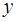 , объясняемую регрессией, в общей дисперсии результативного признака:
, объясняемую регрессией, в общей дисперсии результативного признака: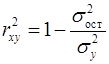 , (15)
, (15)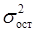 – остаточная дисперсия результативного признака (не объясненная уравнением);
– остаточная дисперсия результативного признака (не объясненная уравнением); – общая дисперсия результативного признака.
– общая дисперсия результативного признака.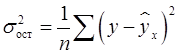 , (16)
, (16) , (17)
, (17) характеризует долю дисперсии
характеризует долю дисперсии 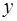 , вызванную влиянием остальных, не учтенных в модели, факторов.
, вызванную влиянием остальных, не учтенных в модели, факторов.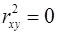 . Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.
. Альтернативная ей гипотеза о значимости уравнения — гипотеза о неравенстве нулю параметров регрессии.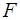 - критерия Фишера, созданного на основе теории дисперсионного анализа. Если расчетное значение F факт с n1= k и n2 = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного (Fтабл) при заданном уровне значимости, то модель считается значимой.
- критерия Фишера, созданного на основе теории дисперсионного анализа. Если расчетное значение F факт с n1= k и n2 = (n - k - 1) степенями свободы, где k – количество факторов, включенных в модель, больше табличного (Fтабл) при заданном уровне значимости, то модель считается значимой. раскладывается на две части – «объясненную» и «необъясненную» (18):
раскладывается на две части – «объясненную» и «необъясненную» (18):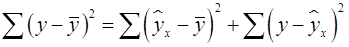 , (18)
, (18)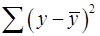 – общая сумма квадратов отклонений;
– общая сумма квадратов отклонений;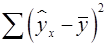 – сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);
– сумма квадратов отклонений, объясненная регрессией (или факторная сумма квадратов отклонений);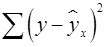 – остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов (необъясненная).
– остаточная сумма квадратов отклонений, характеризующая влияние неучтенных в модели факторов (необъясненная).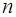 – число наблюдений,
– число наблюдений,  – число параметров при переменной
– число параметров при переменной  ).
).
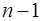
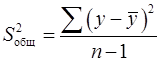
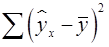

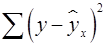
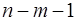

 -критерия Фишера:
-критерия Фишера: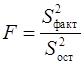 , (19)
, (19) при уровне значимости
при уровне значимости 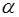 и степенях свободы
и степенях свободы 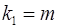 и
и  . При этом, если фактическое значение
. При этом, если фактическое значение 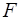 -критерия больше
-критерия больше 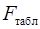 , то признается статистическая значимость уравнения в целом.
, то признается статистическая значимость уравнения в целом.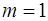 , поэтому
, поэтому 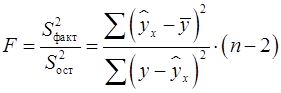 , (20)
, (20)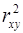 , и в линейной регрессии ее можно рассчитать по следующей формуле (21):
, и в линейной регрессии ее можно рассчитать по следующей формуле (21):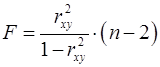 , (21)
, (21) , (22)
, (22)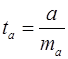 , (23)
, (23)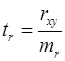 , (24)
, (24)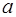 , b, r xy – параметры уравнения регрессии,
, b, r xy – параметры уравнения регрессии,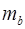 ,
,  ,
,  – стандартные ошибки соответствующих параметров;
– стандартные ошибки соответствующих параметров;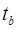 ,
, 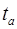 ,
, 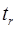 – фактические значения t-статистики или критерия Стьюдента по каждому параметру соответственно.
– фактические значения t-статистики или критерия Стьюдента по каждому параметру соответственно.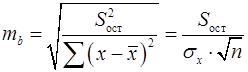 , (25)
, (25)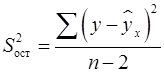 – остаточная дисперсия на одну степень свободы.
– остаточная дисперсия на одну степень свободы.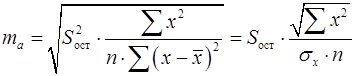 . (26)
. (26)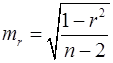 , (27)
, (27) -критерия Стьюдента, определённое по формулам (22), (23), (24) сравнивается с табличным значением при определенном уровне значимости
-критерия Стьюдента, определённое по формулам (22), (23), (24) сравнивается с табличным значением при определенном уровне значимости 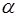 и числе степеней свободы
и числе степеней свободы 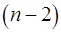 . Если
. Если 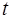 -критерий фактический больше
-критерий фактический больше 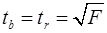 , (28)
, (28)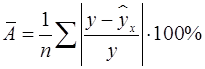 . (29)
. (29)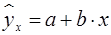 соответствующее значение
соответствующее значение 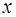 . Таким образом, определяется
. Таким образом, определяется 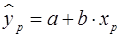 как точечный прогноз у при
как точечный прогноз у при 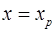 .
. , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определяют доверительный интервал прогноза по формуле (29):
, очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определяют доверительный интервал прогноза по формуле (29):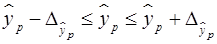 (30)
(30)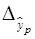 – средняя ошибка прогноза при заданной степени вероятности.
– средняя ошибка прогноза при заданной степени вероятности. , (31)
, (31)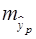 – стандартная ошибка у;
– стандартная ошибка у; – задается самостоятельно, в соответствии со степенью свободы и желаемой вероятностью 1-α.
– задается самостоятельно, в соответствии со степенью свободы и желаемой вероятностью 1-α.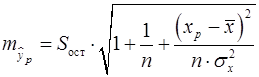 (32)
(32)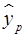 попадает в интервал
попадает в интервал  с вероятностью 1-α.
с вероятностью 1-α.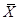 +5%).
+5%).


