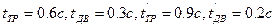Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания к выполнению задачи 1Содержание книги
Поиск на нашем сайте
1. Релейно-контактной схемой называют графическое отображение устройства, в состав которого входят электромагнитные реле, многократные координатные соединители, искатели, а также другие ручные или автоматические переключатели с механическими контактами (ключи, кнопки и т.д.). В релейно-контактных схемах различают реагирующие элементы и контактные цепи. К реагирующим элементам относятся приемные и промежуточные реле, а также исполнительные элементы, непосредственно выполняющие функции, для которых предназначена схема: лампы, электромагниты и т.п., включаемые и выключаемые схемой. Контактными цепями называют цепи, в которых путь для тока образуется при помощи контактов реле или контактов других устройств (например, кнопок, ключей). Входом контактной схемы считается один из полюсов источника электропитания, а выходом- точки подключения контактной схемы к реагирующим элементам. Теория контактных схем оперирует понятиями и закономерностями алгебры логики. В алгебре логики каждый отдельный аргумент может принимать только два значения: “истинно”, условно обозначаемое 1, и “ложно”, условно обозначаемое 0. Применительно к релейно-контактным схемам 1 означает замкнутое, а 0 – разомкнутое состояния контактной цепи. Математическое отображение релейно-контактных схем осуществляется с помощью следующих символических обозначений элементов: прописными буквами А, Б, Х обозначаются обмотки реле, электромагнитов или другие устройства, воспринимающие сигналы; строчными буквами а, б, х обозначаются замыкающие (фронтовые) контакты коммутационных устройств, а строчными буквами с чертой над ними На рис. 1 показано графическое обозначение замыкающего (фронтового) контакта (рис. 1,а) и размыкающего (тылового) контакта (рис. 1,б).
Рисунок 1 - Обозначение фронтового и тылового контактов нейтрального реле в электрических схемах.
Если действия контактов вызывает замыкание цепи, то переменные а, б, х принимают значение 1, и наоборот, переменные а, б, х становятся равными 0, если в результате действия контактов происходит размыкание цепи. Очевидно, что для невозбужденного реле К а=0 и Состав схем и взаимное соединение между контактами описываются с помощью основных операций алгебры логики. Операция «конъюнкция» (И) обозначается знаком умножения и соответствует последовательному включению контактов. Условное обозначение элемента, реализующего функцию f=a b (в дальнейшем знак умножения опускается), представлено на рис. 2,а. Эта функция приобретает значение 1, если оба аргумента равны 1, т.е. цепь будет замкнута, если замкнуты оба последовательно включенных контакта. Операция «дизъюнкция» (ИЛИ) обозначается символом Ú (первая буква союза «или то или другое» латинского языка). Условное обозначение элемента, реализующего функцию f=a Ú b, представлено на рис. 2,б.
Рисунок 2 - Обозначение логических элементов и их реализация логических функций на контактах реле.
Данная функция приобретает значение 1, если хотя бы одно из слагаемых равно 1, т.е. цепь замыкается, когда хотя бы один из контактов замкнут. Операция «отрицание» (НЕ) обозначается чертой над аргументом. Аргумент Введенные символы и логические операции позволяют релейно-контактную схему отобразить структурной формулой. При выполнении п. 1 задачи 1 требуется по заданной структурной формуле построить соответствующую ей релейно-контактную схему. В схеме контакты реле включаются последовательно, если они согласно структурной формуле должны выполнять операцию логического умножения, и параллельно при выполнении операции логического сложения. В качестве примера рассмотрим следующую структурную формулу:
При наличии отрицания (черты) над суммой или произведением каких-либо двух аргументов выражение следует преобразовать с учетом соотношений (13) и (14), приведенных ниже. Тогда
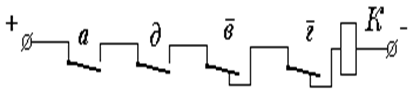
Релейно-контактная схема, соответствующая рассматриваемой структурной формуле, приведена на рис. 3.
Рисунок 3 - Релейно-контактная схема, соответствующая формуле
2.Для упрощения (минимизации) структурных формул необходимо учитывать основные законы и соотношения алгебры логики. Соотношения, согласующиеся с правилами обычной алгебры
x Ú 0=x; (1) x 0=0; (2) x 1=x; (3) x Ú y=y Ú x; (4) x y=y x; (5) x (y z)= (x y) z; (6) x Ú (y Ú z)= (x Ú y) Ú z; (7) x(y Ú z)= x y Ú x z; (8) Соотношения, не имеющие эквивалентов в обычной алгебре:
x Ú 1=1; (9) x Ú x=x; (10) x x=x; (11) x Ú (x y)=x; (12) x (x Ú y)=(x x) Ú (x y)=x Ú (x y)=x; (13) (x Ú y)(x Ú z)=x Ú yz; (14) x Ú x (x Ú y)(x Ú (x y) Ú (x (x (x Ú ( (
Различные конъюнкции, входящие в состав формулы, объединяют в группы, содержащие общие элементы, и выносят эти элементы за скобки; указанные операции полезно производить с таким расчетом, чтобы в скобках оставались выражения вида Члены структурной формулы умножают на единицу, представленную в виде выражения К формуле добавляют новые слагаемые из числа тех, которые имеются; затем группируют и выносят общие члены так, чтобы в скобках оставались выражения равные 1. Осуществим упрощение формулы
Учитывая, что: а) (а Ú е)(а Ú г)= а Ú ег (см. соотношение (6)); б) е Ú в)
Структурная формула релейно-контактной схемы примет вид
3. При построении релейно-контактной схемы по полученной формуле следует учитывать, что логическая операция сложения моделируется параллельным соединением контактов реле, а операция умножения - последовательным соединением контактов. Релейно-контактная схема, соответствующая примерной структурной формуле, приведена на рис. 4.
Рисунок 4 - Релейно-контактная схема, соответствующая формуле
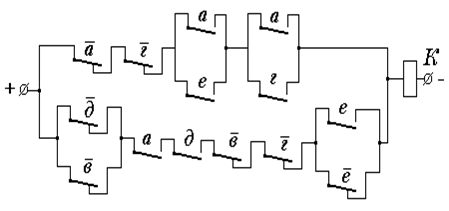
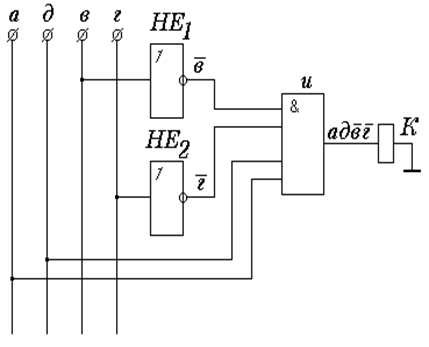
4. Функциональная схема, соответствующая упрощенной форме примерной структурной формулы и выполненная на элементах, реализующих функции отрицания, конъюнкции и дизъюнкции, представлена на рис.5. При построении схемы следует учитывать, что вначале необходимо выполнить операции отрицания, затем операции умножения и, наконец, операции сложения.
Рисунок 5 - Функциональная схема, соответствующая формуле
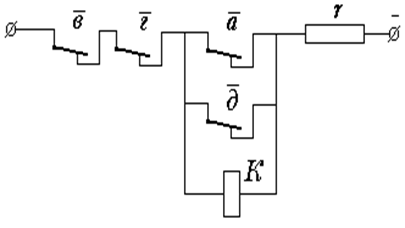
5. Преобразование релейно-контактных схем методом инверсирования позволяет получить эквивалентные по действию схемы, отличающиеся от исходных способом воздействия контактов на реле и другие элементы. При инверсировании релейных схем осуществляется переход от последовательного включения контактных цепей к их параллельному включению относительно обмоток реле или обратный переход от параллельного включения к последовательному с заменой характера действия контактов на обратный. Инверсирование релейных схем часто приводит к включению контактных цепей между полюсами источников тока, что может вызвать короткое замыкание. Поэтому в такие схемы вводятся ограничивающие резисторы, а в соответствующие формулы – символ r. Особенностью инверсирования релейных схем является возможность инверсировать не всю схему, а только отдельные ее части. При этом необходимо, чтобы инверсируемая часть схемы содержала обмотку реле. Операция инверсирования схемы (или части ее) обозначается чертой над структурной формулой, отображающей схему. В рассматриваемом примере в результате упрощений была получена следующая структурная формула схемы:
По заданию требуется преобразовать данную схему так, чтобы в эквивалентной схеме были только замыкающие контакты. Для этого произведем частичное ниверсирование схемы
Схема, соответствующая полученной формуле, приведена на рис. 6.
Рисунок 6 - Релейно-контактная схема, соответствующая формуле
6. Произведем частичное инверсирование схем так, чтобы в эквивалентной схеме были только размыкающие контакты
Для данной формулы схема приведена на рис. 7.
Рисунок 7 - Релейно-контактная схема, соответствующая формуле
Тема 2. Анализ работы релейно-контактных схем с помощью временных диаграмм.
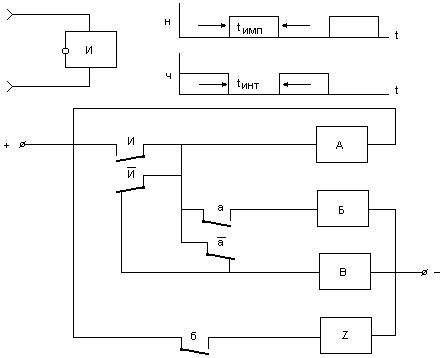
Задача 2. Задана релейно-контактная схема (рис.8), состоящая из приемного реле И, срабатывающего от импульсов постоянного тока, и четырех взаимосвязанных реле А, Б, В, Z, работой которых управляет контакты реле И. Для заданной схемы известно, что при последовательном включении обмоток реле А и Б, а также реле А и В, реле А, Б и А, В будут возбуждены.
Рисунок 8 - Схема взаимосвязанных реле.
Для анализа схемы необходимо: 1. Построить временную диаграмму работы всех реле схемы при поступлении в обмотку реле И двух импульсов с учетом временных параметров реле А, Б, В, Z. Временные параметры этих реле при включении для заданного варианта, определяемого последней цифрой шифра студента, приведены в таблице 2, а временные параметры при выключении для заданного варианта, определяемого предпоследней цифрой шифра студента, приведены в таблице 3.
Таблица 2 – Временные параметры реле при включении
Таблица 3 - Временные параметры реле при выключении
Студенты, сумма цифр шифра которых является нечетной (Н), составляют временную диаграмму при поступлении в обмотку реле И двух импульсов, начиная построение с интервала, а студенты, сумма цифр шифра которых является четной (Ч) – с импульса (Н и Ч на рис.8). Длительность импульсов и интервалов между ними одинакова для всех вариантов и равна Приемное реле И имеет следующие временные параметры, одинаковые для всех вариантов.
В исходном состоянии реле А, Б, В, Z обесточены. Временную диаграмму построить для промежутка времени, равного 25 с. 2. Записать структурные формулы для моментов включения реле А, Б, В, Z, а также тех моментов времени, когда происходят изменения в цепях питания включенных реле (при срабатывании и отпускании реле И).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-11-23; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.105.215 (0.01 с.) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

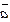 ,
, 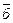 ,
, 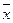 - размыкающие контакты.
- размыкающие контакты.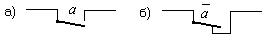
 = 1, а для возбужденного
= 1, а для возбужденного  = 0, а=1.
= 0, а=1.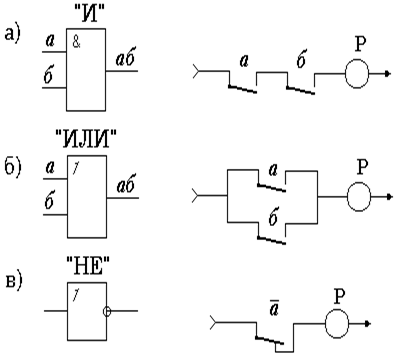
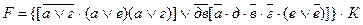
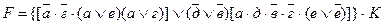
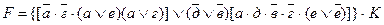
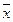 =1; (15)
=1; (15)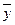 )=x; (17)
)=x; (17)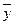 ) Ú y=x Ú y; (19)
) Ú y=x Ú y; (19) )=
)= 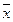
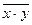 )=
)= 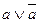 =1 либо выражения, к которым могут быть применены различного рода соотношения.
=1 либо выражения, к которым могут быть применены различного рода соотношения.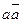 , равную нулю; указанные операции выполняют так, чтобы в структурной формуле образовать группы, поддающиеся дальнейшему упрощению.
, равную нулю; указанные операции выполняют так, чтобы в структурной формуле образовать группы, поддающиеся дальнейшему упрощению.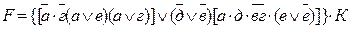 .
.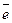 =1 (см. соотношение (7));
=1 (см. соотношение (7));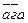 =0;
=0; 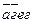 =0;
=0; 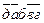 =0 (см. соотношение (8)), получим
=0 (см. соотношение (8)), получим 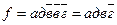 .
.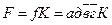
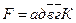
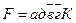
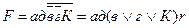 .
.
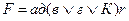
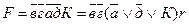 .
.
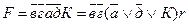 .
.
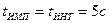 .
.