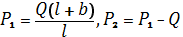Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: особенности расчета ферм при загружении вне узловой нагрузкой.Содержание книги
Поиск на нашем сайте
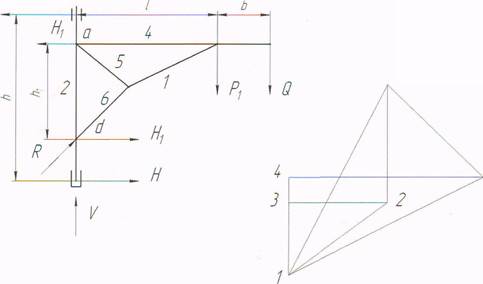
Продолжительность ____2____ часа (Общие положения и правила оформления практических работ.) Рассмотрим построение диаграммы усилия на примере фермы настенно-поворотного крана. Узлы этой фермы из-за конструктивных соображении несовпадают с опорными узлами. Поэтому внеузловую нагрузку Н, необходимо разнести по узлам а и d, соблюдая для нахождения H1 = Нh/h1 законы статики. Аналогично следует поступить с силой Q, заменив ее силами P1 иР2.
Перед построением диаграммы для обозначения действующих сил и усилий в стержнях намечаются соответствующие поля арабскими цифрами 1,2,3,…6. Тогда при обходе узлов по часовой стрелке силы и усилия в стержнях будут обозначаться так: сила Р, как 4-1, усилие в стержне bс как 5-1, а в стержне аb как5-4 и т.д. Построение начинается с того узла, где сходятся не более двух стержней обходя узел по часовой стрелке. Из произвольной точки чертежа откладываем в масштабе силу Р1, сохраняя ее направление (4-1). Далее из точки 1 проводим линию, параллельную стержню сb, а из начала силы Р1, (точка 4) — линию, параллельную стержню ab. Линия пересекается в точке 5. Образованные отрезки прямых 5-1 и 5-4 определяют соответственно принятому масштабу сил усилия в стержнях сb и аb. Усилие в стержне сb направлено к узлу (стержень сжат), а усилие в стержень ab от узла (стержень растянут). Переходим далее к узлу С. Из точки 1 проводим прямую, параллельную стержню dс, а из точки 5 прямую, параллельную- ас. Точка пересечения прямых 6 определит усилие в стержнях. В заключении рассмотрим узел д,, где определим усилие в стержне аd. Стержень аb, испытывающий при движении тележки внеузловую нагрузку, рассчитывается как на поперечный изгиб, так и на действие продольной силы. Аналогично поперечный изгиб учитывается на концах стержня аd длиной (h-h)/2.
СТРУКТУРА МЕТОДИЧЕСКИХ РЕКОМЕНДАЦИЙ ПО ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №___8___ Тема: Расчет однопролетных балок Продолжительность ____2____ часа (Общие положения и правила оформления практических работ.) Формулировка задачи Для одной из однопролетных балок, изображенных на рис. 1.1.1 – 1.1.25 требуется: − построить эпюры внутренних силовых факторов и линии влияния внутренних усилий в сечениях n и k;
− определить усилия в сечениях n и k по линиям влияния от заданной нагрузки и сравнить их с усилиями на эпюрах. Исходные данные для расчета принять из табл. 1.1. Таблица 1.1
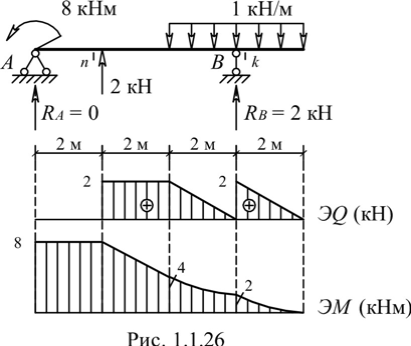
Пример решения задачи Исходные данные: схема балки на рис. 1.1.25; a= 2 м; b= 2 м; c= 2 м; d= 2 м; M= 8 кН м; F= 2 кН; q= 1 кН/м. а) Эпюры внутренних силовых факторов (рис. 1.1.26)
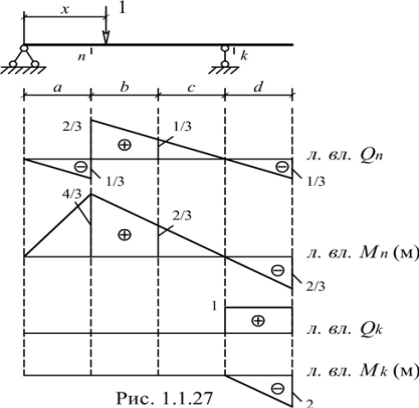
б) Линии влияния внутренних силовых факторов в сечениях n и k (рис. 1.1.27)
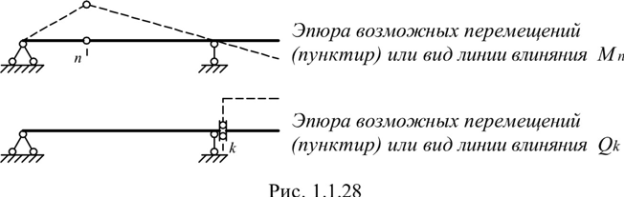
в) Определение внутренних усилий S (изгибающего момента или поперечной силы) в сечениях n и k по формуле влияния: S = M ⋅tgα + F ⋅ y + q ⋅ω, где M – сосредоточенный момент («+» - направлен по часовой стрелке, «-» - направлен против часовой стрелки); α – наклон линии влияния в месте приложения M; F – сосредоточенная сила («+» - направлена вниз, «-» - направлена вверх); y – ордината линии влияния под силой; q – интенсивность распределенной нагрузки («+» - направлена вниз, «-» - направлена вверх); ω – площадь линии влияния под нагрузкой. M кНм, = (−8) ⋅ (−1/ 6) + (−2) ⋅ (2 / 3) +1⋅0 = 0 n Q, = (−8) ⋅0 + (−2) ⋅0 +1⋅ (−2) = −2 k M кНм, = (−8) ⋅0 + (−2) ⋅0 +1⋅ 2 = 2 k Q кН. Значение усилий совпали с соответствующими усилиями на эпюрах. Пояснение к решению задачи 1. Для построения линий влияния в балках целесообразно воспользоваться статико-кинематическим методом. Суть метода заключается в том, что вначале определяется вид линии влияния. Для этого из балки удаляется связь, линию влияния усилия в которой требуется построить. В полученном таким образом механизме с одной степенью свободы строится эпюра возможных перемещений (рис. 1.1.28). В теории линий влияния на основе принципа возможных работ доказано, что вид линии влияния совпадает с очертанием этой эпюры. При известном очертании линии влияния любую ее ординату несложно вычислить из законов статики. Для этого достаточно установить единичный груз над ординатой, отделить часть балки, содержащей искомое усилие, и рассмотреть равновесие этой части.
Примечание. Знак линии влияния определиться автоматически, если возможное перемещение механизму задать в направлении, совпадающем с положительным направлением искомого усилия.
2) При определении усилий по линиям влияния следует помнить, что внешний сосредоточенный момент вносится в формулу влияния со знаком «+», если направлен по часовой стрелке, внешняя сосредоточенная сила и распределенная нагрузка со знаком «+», если направлены вниз. Такие правила приняты при выводе формулы влияния. Знак же тангенса определяется обычным образом, т.е. в первой и третьей четвертях он положительный (если линия влияния не перевернута).
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-12-19; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.124.80 (0.01 с.) |