
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные виды напряжённо-деформированного состояния (НДС)
Экзаменационный билет № 12 1. Нагельные соединения. Классификация. Признаки напряженно-деформированного состояния. Расчет.
Нагелем называется длинный гибкий стержень (пластинка), который, соединяя элементы деревянных конструкций между собой, препятствует их взаимному сдвигу. Сам нагель при этом работает преимущественно на поперечный изгиб.
Нагели используются в стыках растянутых элементов, в составных стержнях и балках на податливых связях, в узлах деревянных ферм. Нагельные соединения отличаются податливостью: усилия распределяются между нагелями достаточно равномерно, что способствует повышению надежности таких соединений. Простота изготовления и надежность нагельных соединений обеспечили их распространение и в современном строительстве. Классификация нагелей: – по материалу: стальные (С 245, С 255); деревянные (из твердых пород древесины: дуба, березы); пластмассовые (из конструкционных стеклопластиков, типа АГ-4с);
– по форме поперечного сечения: цилиндрические (болты, штыри, гвозди, шурупы, глухари – шурупы большого диаметра с головкой под ключ); пластинчатые (нагели Деревягина);
– по способу постановки: собственно нагели, устанавливаемые в предварительно просверленные отверстия, при этом диаметр отверстия равен диаметру нагеля (dотв=dнаг); нагели, завинчиваемые в предварительно просверленные отверстия, при этом dотв= 0,8dнаг (шурупы и глухари); нагели диаметром менее 6 мм (гвозди), забиваемые в древесину без предвари-тельного сверления отверстий;
– по способу приложения внешних сил и числу швов, пересекаемых одним нагелем, различают два вида нагельных соединений (рис.2.5): симметричные (двух- и многосрезные) и несимметричные (одно-, двух- и многосрезные). Напряженно-деформированное состояние — совокупность напряжений и деформаций, возникающих при действии на материальное тело внешних нагрузок, температурных полей и других факторов. Совокупность напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде тензора напряжений, {\displaystyle T_{\sigma }} {\displaystyle {T_{\varepsilon }}=\left[{\begin{matrix}\varepsilon _{x}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{y}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{z}\\\end{matrix}}\right]}
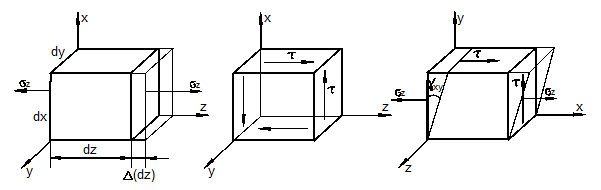
Основные виды напряжённо-деформированного состояния (НДС) До сих пор мы рассматривли в основном простейшие виды НДС – растяжение – сжатие, плоский чистый сдвиг и их комбинацию (рис. 3.3).
а) б) в) Рис. 3.3
Они встречаются при растяжении и сжатии стержня и его кручении, а также при изгибе (рис. 3.4). При растяжении и сжатии (рис. 3.4, а) осевая
а) Растяжение б) Кручение
в) Изгиб Рис. 3.4
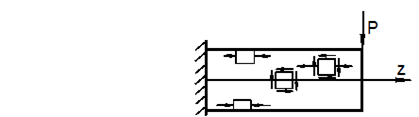
При плоском чистом сдвиге (рис. 3.4, б) деформация сдвига
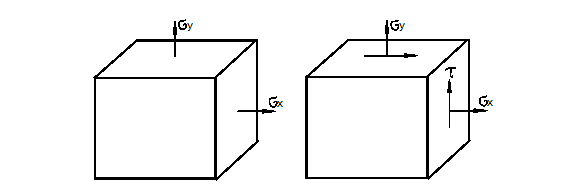
Часто на практике встречаются двухосное растяжение и его комбинация с чистым сдвигом (рис. 3.5).
а) б) Рис. 3.5
В последнем случае состояние называют плоским напряжённым состоянием. Оно возникает в тонкостенных элементах конструкций, таких как плиты (пластины) и оболочки (рис. 3.6). При двухосном растяжении деформации в направлениях x и y могут быть найдены на основании законов (11) для одноосного растяжения. Представим
а) б) Рис. 3.6
Для плоского напряжённого состояния (рис. 3.6, б) с учётом (12) получаем:
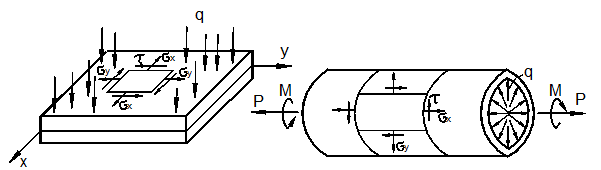
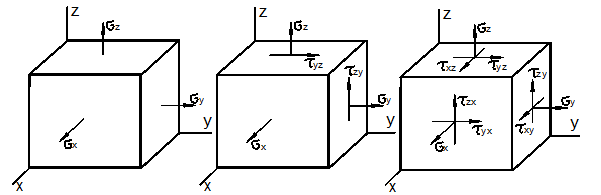
При трёхосном растяжении (рис. 3.7, а) на основании законов (11) аналогичным образом получаем:
а) Трёхосное б) Плоская в) Объёмное напряжённое растяжение деформации состояние Рис. 3.7
Если сложить соотношения (15), то получим закон упругого изменения объёма:
где
На практике часто встречается напряжённое состояние, изображённое на рис. 3.7, б. Оно возникает в удлинённых телах со стеснённой в этих направлениях деформацией. Примером могут служить подпорная стенка, тело плотины, железнодорожный рельс и др. В этих случаях призматическое тело как бы зажато между двумя опорами, а нагрузка вдоль тела остаётся неизменной (рис. 3.8).
а) б) в) г) Рис. 3.8
Произвольная точка А тела при деформации остаётся лежать в одной плоскости, параллельной плоскости x, y. Напряжённое состояние отличается от плоского тем, что возникает напряжение
Характерным примером возникновения объёмной НДС могут служить контактные задачи. Например, задачи о контакте колёс вагона с рельсами, задача о вдавливании шарика в подшипнике, шаровой опоры в фундамент и др. (рис. 3.9, а).
а) б) Рис. 3.9
Кубик, опущенный в воду (рис. 3.9, б), будет испытывать всестороннее сжатие напряжениями
где Другим близким примером могут служить полупространства, представляющие собой модель грунтовой среды. Слой грунта толщины z оказывает на нижележащие слои давление
откуда
где
называется коэффициентом бокового давления среды. Если
При этом изменение объёма
Рис. 3.10
Его можно разложить на сумму двух состояний – трёхосное растяжение и сложный сдвиг в трёх координатных плоскостях. На основании принципа независимости действия сил (напряжений), используя (19) и
Уравнения (20) можно разрешить относительно напряжений:
где
Коэффициент Из (20), (21) следует ещё одна форма записи обобщённого закона Коши – Гука в форме трёх законов: 1. Закон упругого изменения объёма Складывая в (20) относительные удлинения, получаем:
где 2. Закон упругого формоизменения Составим на основании (20), (23) выражение:
Аналогично можно найти разности
представляющие закон упругого формоизменения. Соотношения (24) связывают компоненты девиаторов напряжений и деформаций. 3. Закон упругого упрочнения материала Величину
называют модулем девиатором напряжений. Из (24) следует:
Подставляя полученные выражения в (25), находим:
где величина
носит название модуля- девиатора деформаций. Соотношение (26) выражает собой закон упругого упрочнения материала. В частном случае простого растяжения
Таким образом, закон упругого упрочнения (26) с точностью до постоянного множителя
2. Деревянные перекрытия. Оформление расчетных материалов расчетно-графической работы Четкие правила унифицируют письменное составление расчетов для каждой РГР, вне зависимости от предмета исследования. В случае расчетных материалов действуют правила: · Символы для составления формул должны обязательно соответствовать международной системе единиц (СИ); · Числовые значение величин в формуле обязательны; · Итоговый результат требует указание размерности, промежуточные вычисления не указываются; · Степень точности числовых значений до тысячных; · Формулы разделяются точкой с запятой, если между ними нет текста. Оформление графических материалов РГР Основа расчетно-графической работы это обилие схем, графиков и формул. Они переплетаются с пояснительным текстом, и вместе создают грамотный и логично-построенный результат. Правила соответствуют ГОСТ и подразумевают:
· Обязательно наличие схемы перед каждым новым расчетом. · Нумерация схем сквозная. Пример: 1 – Расчетная схема и название схемы. · Схемы размещаются так, чтобы удобно было их рассматривать и согласно размеру страницы. · Переменные величины в диаграммах указываются в виде шкал и в произвольном масштабе. · На осях и координатах диаграмм указываются делительные штрихи. · Поле графика должно быть заполнено согласно масштаба координатов. · Надписи на схемах и диаграммах выполняют чертежным шрифтов по ГОСТ 2.304-81. Следуя четкому и понятному алгоритму оформления, можно составить грамотную РГР. Польза ее составления заключается в получении практического опыта и оценки за труды. Оформлять лучше сразу же в процессе создания, чтобы экономить время и сделать все корректно.
Экзаменационный билет № 12 1. Нагельные соединения. Классификация. Признаки напряженно-деформированного состояния. Расчет.
Нагелем называется длинный гибкий стержень (пластинка), который, соединяя элементы деревянных конструкций между собой, препятствует их взаимному сдвигу. Сам нагель при этом работает преимущественно на поперечный изгиб.
Нагели используются в стыках растянутых элементов, в составных стержнях и балках на податливых связях, в узлах деревянных ферм. Нагельные соединения отличаются податливостью: усилия распределяются между нагелями достаточно равномерно, что способствует повышению надежности таких соединений. Простота изготовления и надежность нагельных соединений обеспечили их распространение и в современном строительстве. Классификация нагелей: – по материалу: стальные (С 245, С 255); деревянные (из твердых пород древесины: дуба, березы); пластмассовые (из конструкционных стеклопластиков, типа АГ-4с);
– по форме поперечного сечения: цилиндрические (болты, штыри, гвозди, шурупы, глухари – шурупы большого диаметра с головкой под ключ); пластинчатые (нагели Деревягина);
– по способу постановки: собственно нагели, устанавливаемые в предварительно просверленные отверстия, при этом диаметр отверстия равен диаметру нагеля (dотв=dнаг); нагели, завинчиваемые в предварительно просверленные отверстия, при этом dотв= 0,8dнаг (шурупы и глухари); нагели диаметром менее 6 мм (гвозди), забиваемые в древесину без предвари-тельного сверления отверстий;
– по способу приложения внешних сил и числу швов, пересекаемых одним нагелем, различают два вида нагельных соединений (рис.2.5): симметричные (двух- и многосрезные) и несимметричные (одно-, двух- и многосрезные).
Напряженно-деформированное состояние — совокупность напряжений и деформаций, возникающих при действии на материальное тело внешних нагрузок, температурных полей и других факторов. Совокупность напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде тензора напряжений, {\displaystyle T_{\sigma }} {\displaystyle {T_{\varepsilon }}=\left[{\begin{matrix}\varepsilon _{x}&\varepsilon _{xy}&\varepsilon _{xz}\\\varepsilon _{yx}&\varepsilon _{y}&\varepsilon _{yz}\\\varepsilon _{zx}&\varepsilon _{zy}&\varepsilon _{z}\\\end{matrix}}\right]} Основные виды напряжённо-деформированного состояния (НДС) До сих пор мы рассматривли в основном простейшие виды НДС – растяжение – сжатие, плоский чистый сдвиг и их комбинацию (рис. 3.3).
а) б) в) Рис. 3.3
Они встречаются при растяжении и сжатии стержня и его кручении, а также при изгибе (рис. 3.4). При растяжении и сжатии (рис. 3.4, а) осевая
а) Растяжение б) Кручение
в) Изгиб Рис. 3.4
При плоском чистом сдвиге (рис. 3.4, б) деформация сдвига
Часто на практике встречаются двухосное растяжение и его комбинация с чистым сдвигом (рис. 3.5).
а) б) Рис. 3.5
В последнем случае состояние называют плоским напряжённым состоянием. Оно возникает в тонкостенных элементах конструкций, таких как плиты (пластины) и оболочки (рис. 3.6). При двухосном растяжении деформации в направлениях x и y могут быть найдены на основании законов (11) для одноосного растяжения. Представим
а) б) Рис. 3.6
Для плоского напряжённого состояния (рис. 3.6, б) с учётом (12) получаем:
При трёхосном растяжении (рис. 3.7, а) на основании законов (11) аналогичным образом получаем:
а) Трёхосное б) Плоская в) Объёмное напряжённое растяжение деформации состояние Рис. 3.7
Если сложить соотношения (15), то получим закон упругого изменения объёма:
где
На практике часто встречается напряжённое состояние, изображённое на рис. 3.7, б. Оно возникает в удлинённых телах со стеснённой в этих направлениях деформацией. Примером могут служить подпорная стенка, тело плотины, железнодорожный рельс и др. В этих случаях призматическое тело как бы зажато между двумя опорами, а нагрузка вдоль тела остаётся неизменной (рис. 3.8).
а) б) в) г) Рис. 3.8
Произвольная точка А тела при деформации остаётся лежать в одной плоскости, параллельной плоскости x, y. Напряжённое состояние отличается от плоского тем, что возникает напряжение
Характерным примером возникновения объёмной НДС могут служить контактные задачи. Например, задачи о контакте колёс вагона с рельсами, задача о вдавливании шарика в подшипнике, шаровой опоры в фундамент и др. (рис. 3.9, а).
а) б) Рис. 3.9
Кубик, опущенный в воду (рис. 3.9, б), будет испытывать всестороннее сжатие напряжениями
где Другим близким примером могут служить полупространства, представляющие собой модель грунтовой среды. Слой грунта толщины z оказывает на нижележащие слои давление
откуда
где
называется коэффициентом бокового давления среды. Если
При этом изменение объёма
|
|||||||||
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.137.150 (0.009 с.) |

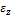 и поперечные деформации
и поперечные деформации 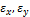 определяются законами Гука и Пуассона:
определяются законами Гука и Пуассона: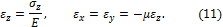
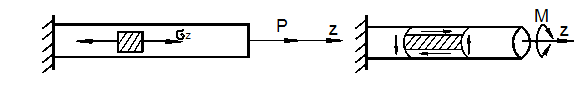

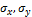 ) в виде суммы деформаций в каждом из направлений x и y от этих сил:
) в виде суммы деформаций в каждом из направлений x и y от этих сил: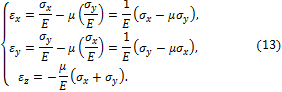
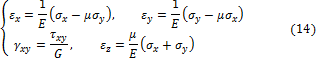
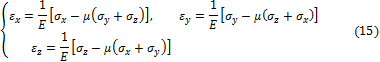
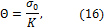
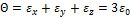 – относительное изменение объёма, (17)
– относительное изменение объёма, (17)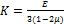 – модуль объёмной деформации. (18)
– модуль объёмной деформации. (18)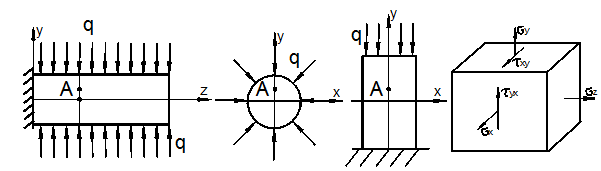
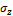 . Соответствующее деформированное состояние тела носит название плоской деформации. Относительные деформации определяются соотношениями закона Гука, полученные использованием принципа независимости действия сил (напряжений). Накладывая на соотношения (5) при трёхосном растяжении плоский чистый сдвиг с напряжениями
. Соответствующее деформированное состояние тела носит название плоской деформации. Относительные деформации определяются соотношениями закона Гука, полученные использованием принципа независимости действия сил (напряжений). Накладывая на соотношения (5) при трёхосном растяжении плоский чистый сдвиг с напряжениями 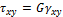 , получаем:
, получаем: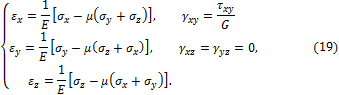
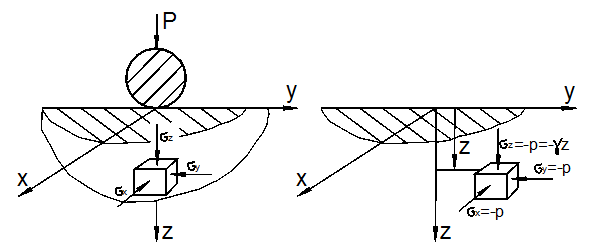
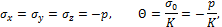
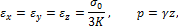
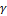 - удельный вес воды.
- удельный вес воды.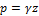 , где
, где 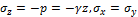 . Деформации
. Деформации 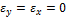 , и согласно (12):
, и согласно (12):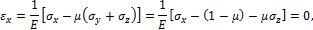
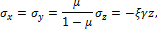
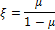
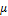 =0,5, то
=0,5, то 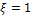 и частица будет испытывать всестороннее сжатие, т.к.:
и частица будет испытывать всестороннее сжатие, т.к.: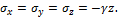
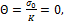 так как
так как 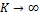 . Такая среда называется несжимаемой.
. Такая среда называется несжимаемой.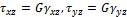 , получаем:
, получаем: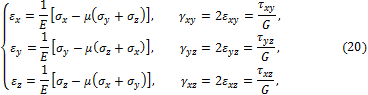
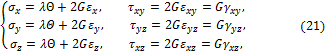
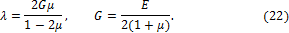
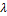 называют модулем Коши – Ламе.
называют модулем Коши – Ламе.
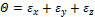 - относительное изменение объёма,
- относительное изменение объёма, 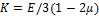 - модуль деформации.
- модуль деформации.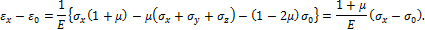
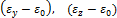 . В результате получаем соотношения
. В результате получаем соотношения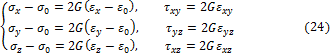
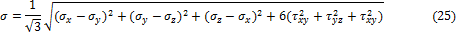
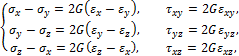

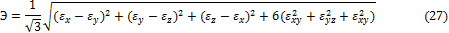
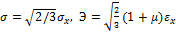 и соотношение (26) принимает вид
и соотношение (26) принимает вид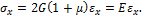
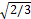 совпадает графически с упругим участком диаграммы растяжения.
совпадает графически с упругим участком диаграммы растяжения.


