
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные операции над векторами. Умножение вектора на число, его свойства, условие коллинеарности векторов.Содержание книги
Поиск на нашем сайте
Суммой
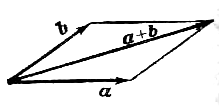
Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы
Сложение многих векторов производится при помощи последовательного применения правила треугольника (см. рис. 3, где изображено построение суммы четырех векторов
Разность Произведение Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Имеют место следующие две основные теоремы о проекциях векторов: 1). Проекция суммы векторов на какую-нибудь ось равна сумме ее проекций на эту же ось:
2). При умножении вектора на число его проекция умножается на то же число:
В частности, если
то
и
Если
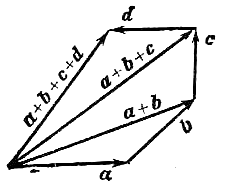
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. Признаком коллинеарности двух векторов
является пропорциональность их координат:
Тройка векторов 1). Вектор 2). Каждый из векторов 3). Векторы Каким бы ни был вектор
коэффициенты этого разложения являются координатами вектора Произведением вектора 1) 2) и обозначается Теорема. (Свойства умножения вектора на число.) 1. Свойство ассоциативности: равенство 2. Свойство дистрибутивности умножения относительно сложения чисел:
3. Свойство дистрибутивности умножения относительно сложения векторов:
4. Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости Необходимым и достаточным условием коллинеарности ненулевого вектора
|
||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 143; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.005 с.) |

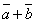 двух векторов
двух векторов  и
и  называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора 
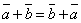 .
.
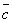 ,
, 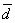 ).
).
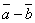 двух векторов
двух векторов  . Легко видеть, что
. Легко видеть, что  . Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».
. Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».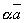 (или также
(или также 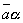 ) вектора
) вектора  называется вектор, модуль которого равен произведению модуля вектора
называется вектор, модуль которого равен произведению модуля вектора 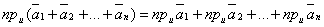
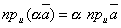 .
. ,
, 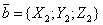 ,
,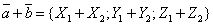 ,
, .
. , то для любого числа
, то для любого числа 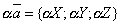 .
.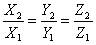 .
.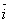 ,
, 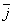 ,
,  называется координатным базисом, если эти векторы удовлетворяют следующим условиям:
называется координатным базисом, если эти векторы удовлетворяют следующим условиям: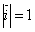 ,
,  ,
, 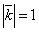 .
. ;
;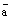 на действительное число
на действительное число  называется вектор
называется вектор 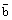 , удовлетворяющий следующим двум условиям:
, удовлетворяющий следующим двум условиям: ;
; , если
, если  и
и 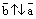 , если
, если 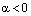 ;
;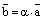 .
.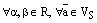 верно
верно .
.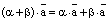 .
. верно равенство
верно равенство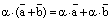 .
. верно равенство
верно равенство 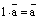 .
. и вектора
и вектора 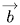 является существование такого числа
является существование такого числа 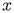 , которое удовлетворяет равенству
, которое удовлетворяет равенству 



