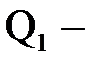Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методика проведения работы с помощью математической модели нестационарной теплопроводности при нагреве различных материаловСодержание книги
Поиск на нашем сайте
Для проведения расчетов необходимо:
1.Вписать в программу Ф.И.О. студента, код группы 2.Ввести заданные значения плотности, теплопроводности и теплоемкости материала 3.Распечатать программу и запустить счет 4. Ввести периодичность печати А1=500 циклов счета, что соответствует 5 секундам реального времени 5. Нажать на клавишу ENTER 6. Повторить счет не менее 12 раз 7.Распечатать результаты вычислений и перенести их в таблицу 2. 8. Построить поля температур для различных моментов времени 9. Построить график зависимости температур в характерных точках пластины от времени Таблица 5.2– Результаты вычислений
Рисунок 5.1 – Блок-схема программы расчета СПИСОК ОБОЗНАЧЕНИЙ В ПРОГРАММЕ а= А1 – периодичность по времени, с. А2=Dt - шаг интегрирования, с А3 – счетчик времени, с В – коэффициент теплоотдачи, Вт/м2К В1- длина образца, м В2 – ширина образца, м В3 – толщина, м В4=Dх – продольный размер расчетной ячейки, м Вi = Fo = М1(J)- поле температур, оС М17(J) =Т(J)+DТ- вновь рассчитанное поле температур, оС N- число расчетных ячеек, j=0- холодный конец, j-59 – нагретый Р1=Ср- теплоемкость образца, Дж/кг К Р8= Р9= Р11= Р12= Р13=Dх2 - промежуточная величина
Р14= Т – температура нагретого конца стержня (образца), оС Т1- температура окружающей среды, оС Т3 =l - теплопроводность образца, Вт/м К Т9=r - плотность образца, кг/м3
конвекцией, Вт/м3 ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
1. Рассчитать значения безразмерной температуры и критерия Фурье и построить график изменения q в средней части пластины от безразмерного времени (Fo). q = (T3-T2) / (T1-T2) 2. Вычислить значение коэффициента теплопроводности образца
где Q- мощность нагрева на стационарном режиме теплопроводности, Q = I × U
3. Сравнить результаты численного исследования и лабораторного эксперимента 4. Проанализировать полученные результаты и сделать выводы о характере нестационарного процесса, влиянии теплоемкости, плотности, теплопроводности и геометрических размеров образца на характеристики нестационарного процесса. 5. Сделать выводы об информативности численного и экспериментального методов исследования нестационарной теплопроводности, возможностях применений подходов, использованных в настоящей работе, в других задачах.
Контрольные вопросы:
1. Что входит в полную математическую постановку задачи нестационарной теплопроводности? 2. Запишите разностный аналог второй производной температуры от линейной координаты. 3. По какому закону изменяется температура по времени при нагревании пластины? 4. У каких материалов стационарный режим наступает быстрее? 5. Какие обобщенные координаты используются для универсального описания нестационарной теплопроводности? Лабораторная работа 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.117.122 (0.007 с.) |

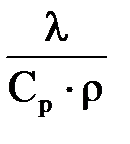 - коэффициент температуропроводности
- коэффициент температуропроводности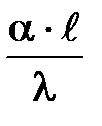 - критерий Био
- критерий Био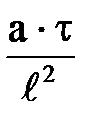 - критерий Фурье (безразмерное время)
- критерий Фурье (безразмерное время)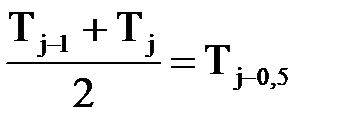
 – температура на границе ячеек j и j-1
– температура на границе ячеек j и j-1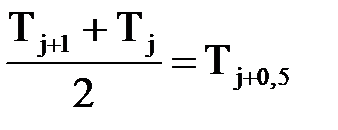 – температура на границе ячеек j и j+1
– температура на границе ячеек j и j+1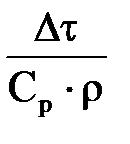 - промежуточная величина
- промежуточная величина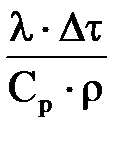 - промежуточная величина
- промежуточная величина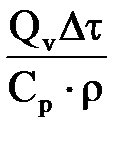 - количество теплоты, отданное конвекцией за время Dt
- количество теплоты, отданное конвекцией за время Dt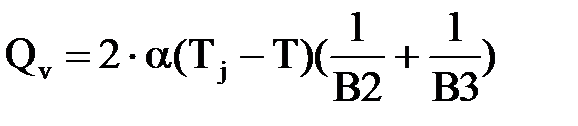 - мощность теплового потока отдаваемого
- мощность теплового потока отдаваемого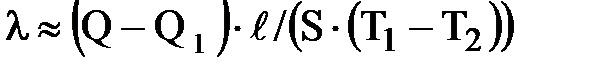
 ,
,