
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные параметры закона РелеяСодержание книги
Поиск на нашем сайте
Среднее арифметическое Rср переменной случайной величины (эксцентриситета, биения, разностенность и др.), ее среднее квадратическое отклонение σR и среднее квадратическое отклонение σ0 значений координат X и Y конца радиус-вектора R связаны между собой следующими соотношениями:
(2)
Rср=1,92∙σR=1,253∙σ0 (3)
Фактическое поле рассеивания значений переменной величины радиус-вектора R (эксцентриситета, биения, разностенность и др.) находят из выражений: ∆=5,252∙σR; (4)
∆=3,44∙σ0; (5)
При анализе погрешностей обработки конкретных заготовок расчетное значение среднего квадратического отклонения σR радиус вектора определяют по величине среднего квадратичного S, установленного путем измерений партии – выборки деталей и последующего вычисления по формуле (6)
где S – среднее квадратическое отклонение; Xi – текущий действительный размер;
mi – частота (количество заготовок данного интервала размеров) n – количество заготовок в партии; Для перехода от эмпирической величины S к расчетной σR используют уравнение σR=p∙S, (8) где p –поправочный коэффициент, учитывающий погрешность определения среднего квадратического отклонения при малых размерах партии измеренных заготовок N см. таблицу №2. [1]
Таблица №2
Обработка результатов измерений. Построение практической кривой распределения Построение производиться в следующей последовательности: 6.1.1. Из всего ряда фактических размеров выбирают наибольшее отклонение параметра, характеризующего размах: R=Xmax 6.1.2. Определяют величину интервала h, которая берется в пределах 1/7…1/10 величины размаха R: h= (1/7…1/10) ∙R (9) причем величина первого интервала, который начинается в точке 0, должна быть вдвое меньше каждого из последующих интервалов. При построении практической кривой рассматривают частоты интервалов как средние точности распределения на них, поэтому частота не начального интервала, который вдвое короче остальных, должна быть удвоена.
6.1.3. Весь ряд замеров разбивают на группы отклонений с интервалом h и определяют абсолютную частоту mi попадания размеров в каждый интервал. Результаты заносят в таблицу №3 Таблица №3
6.1.4. В координатах (mi; xi) из середины каждого интервала откладывается абсолютная частота попадания в заданный интервал mi. Полученные точки соединяются прямыми линиями.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.70.133 (0.008 с.) |

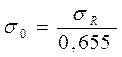
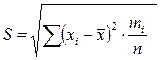 =
= 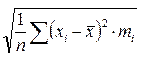 , (6)
, (6)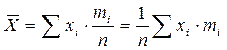 (7)
(7)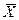 – среднее арифметическое значение действительных размеров заготовок данной партии;
– среднее арифметическое значение действительных размеров заготовок данной партии;


