
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равновесие на рынке труда и капиталаСодержание книги Поиск на нашем сайте
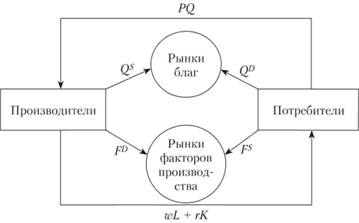
Пример 7.1 Допустим, что отраслевые функции спроса и предложения двух взаимозаменяемых благ А и В имеют вид:
Вследствие частичной взаимозаменяемости благ при повышении цены одного из них растет спрос на другое благо. Поскольку при выпуске благ применяются одни и те же факторы производства, то в случае повышения цены одного из благ производители увеличивают его предложение за счет сокращения предложения другого блага. Приравняв друг к другу спрос и предложение на рынке блага А, найдем его равновесную цену, зависящую от цены блага В:
Уравнение (7.1) определяет цену, которая обеспечивает равенство объемов спроса и предложения на рынке блага А при любой цене блага В, в том числе и неравновесной. Все значения Р A, которые обеспечивают равновесие на рынке блага А при неравновесных значениях Р B, являются ценами частичного равновесия: на одном рынке равновесие, на другом нет. Так, если Р B = 25, то цена Р A = 8,4 + 0,6 × 25 = 23,4 уравнивает объемы спроса и предложения на рынке блага А:
хотя на рынке блага В существует дефицит:
Чтобы найти то значение Р A, которое соответствует совместному равновесию на обоих рынках, нужно предварительно определить множество цен частичного равновесия на рынке блага В. Она определяется из условия равновесия на этом рынке:
Решение системы уравнений (7.1) и (7.2) дает значения цен, обеспечивающих совместное равновесие на обоих рынках:
Проверим состояние рынков при этих ценах:
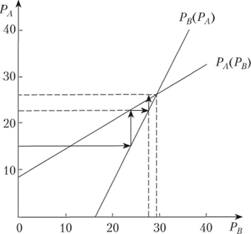
Наглядно процесс установления совместного равновесия на двух рассматриваемых рынках изображен на рис. 7.1.
Рис. 7.1. Устойчивое совместное равновесие на двух рынках Допустим, на рынке блага A объемы спроса и предложения совпали при Р A = 15. Тогда в соответствии с (7.2) на рынке блага В равновесие установится при 23,8. Но тогда по (7.1) для сбалансированности рынка блага А требуется Р A = 22,7. Через несколько шагов установится совместное равновесие при Р A = 26; Р B = 29,3. Рисунок 7.1 показывает, что совместное равновесие при заданных функциях спроса и предложения является устойчивым. Однако так бывает не всегда. Если бы спрос и предложения на рынках отображался следующими функциями:
то совместное равновесие на обоих рынках обеспечивали бы цены Р A = 2,7; Р B = 2. Но это неустойчивое равновесие, что иллюстрирует рис. 7.2. При определенных параметрах функций спроса и предложения прямые Р A(Р В) и Р В(Р A) вообще могут не пересечься в квадранте положительных цен; это означает, что совместного равновесия нс может быть.
Если достижение совместного равновесия хотя бы только на двух рынках связано с выполнением целого ряда условий, то возможно ли существование общего экономического равновесия в экономике с множеством рынков благ и факторов производства? Для ответа на этот вопрос нужна модель, описывающая функционирование всего национального хозяйства. В ней кроме взаимодействия производителей и потребителей на рынках благ необходимо отразить взаимодействие между субъектами общественного хозяйства на рынках факторов производства, где формируются доходы потребителей, определяющие их спрос на блага. Первым экономистом, построившим такую модель, был Леон Вальрас[1].
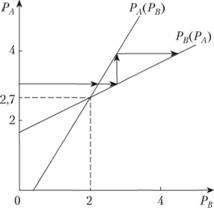
Рис. 7.2. Неустойчивое совместное равновесие на двух рынках Общее экономическое равновесие (ОЭР). С включением в модель рынков факторов производства экономика предстает в виде замкнутой системы, схематически представленной на рис. 7.3.
Рис. 7.3. Взаимозависимость рынков благ и факторов производства На рынках благ домашние хозяйства осуществляют расходы, а фирмы получают доходы; на рынках факторов, наоборот, домашние хозяйства имеют доходы в виде заработной платы и дивидендов, а фирмы несут расходы по оплате труда и капитала. Предполагается, что экономические агенты не делают сбережений, т.е. все доходы расходуются на покупку благ и факторов производства. Так, если в экономике используются два фактора производства (L, К) и производятся два блага (Л, В), то для каждого экономического субъекта выполняется равенство
Равенство (7.3) означает, что расходы субъекта на покупку благ и факторов производства (левая часть) равны его доходам от продажи благ и предоставления услуг труда и капитала (правая часть). Представим его в другом виде:
В скобках представлен результат сделок экономического субъекта на каждом из рынков; их суммарный результат равен нулю. Сложив результаты сделок всех участников на всех рынках, получим следующее равенство:
Каждое из слагаемых правой части равенства (7.4) характеризует конъюнктуру на отдельном рынке: если оно равно нулю, то на рынке достигнуто равновесие; в противном случае на рынке существует дефицит или избыток. Из равенства (7.4) вытекают два важных свойства национальной экономики.
Во-первых, при отсутствии общего экономического равновесия сумма избытков на одних рынках равна сумме дефицитов на других рынках. Во-вторых, если некоторая система цен обеспечивает равновесие на любых трех рынках (превращает в нуль разность в любых трех скобках), то равновесие будет и на четвертом рынке (нулю будет равна и разность в четвертой скобке). Этот вывод, верный для любого числа рынков, назван законом Вальраса. В соответствии с законом Вальраса система из п уравнений, представляющих условия равновесия на п взаимосвязанных рынках, содержит только п – 1 независимых уравнений и потому не имеет однозначного решения. Для преодоления этого препятствия необходимо либо добавить еще одно независимое уравнение, либо исключить одно неизвестное. Первый вариант используется в макроэкономике; в качестве дополнительного берется уравнение, определяющее равенство спроса и предложения на рынке денег. В микроэкономике применяется второй вариант. Для объяснения микроэкономических явлений достаточно знать систему относительных цен, которая основана на том, что определенное количество одного товара служит масштабом цен при измерении ценности всех других товаров. Цена избранного товара принимается за единицу и тогда число неизвестных оказывается равным числу независимых уравнений. Как известно из математики, само по себе такое равенство не гарантирует существования решения соответствующей системы уравнений, особенно если искомые переменные должны иметь положительные значения. В этом мы могли убедиться в предыдущем разделе данной главы. Однако К. Эрроу и Г. Дебре доказали, что модель Л. Вальраса имеет однозначное решение, если:
Пример 7.2 Экономика состоит из двух представительных домашних хозяйств, потребляющих два блага (А и В), и двух представительных фирм, одна из которых производит благо А, другая – благо В. Хозяйство ведется в условиях совершенной конкуренции, поэтому каждый из его участников воспринимает цены в качестве экзогенных параметров. Предпочтения домашних хозяйств относительно потребляемых благ и свободного времени отображаются следующими функциями полезности:
Бюджеты домашних хозяйств образуются из заработной платы и доходов от капитала. У первого домашнего хозяйства имеется К 1 = 40 капитала, а у второго – К 2 = 60. Поэтому бюджетные уравнения домашних хозяйств имеют вид:
Технология производства благ отображается функциями:
Таковы исходные данные. По ним, опираясь на изученное содержание предыдущих глав, нужно определить:
Приступим к решению этой задачи. Так как предпочтения потребителей отображаются функцией полезности Стоуна, то их функции спроса на блага и предложения труда выводятся так, как показано в Приложение к гл. 3; в роли блага С теперь выступает свободное время (280 -
Функции спроса фирм на труд и капитал выведены в параграфе 6.2. В рассматриваемом примере они получаются такими:
Подставив найденные величины в функцию средних затрат длительного периода
Средние затраты у обеих фирм оказались неизменными при любом выпуске из-за того, что их технологии имеют неизменную отдачу от масштаба. Следовательно, равновесные цены благ будут равны средним затратам:
Добавим к равенствам (7.5) условия равновесия на рынке капитала, труда и рынке блага А:
В соответствии с законом Вальраса при равновесии на этих трех рынках на рынке блага В тоже будет равновесие. В системах (7.5)-(7.8) – пять независимых уравнений с шестью неизвестными. Приняв w = 1, из решения системы получаем значения остальных пяти переменных: r = 2,26; Р A = 2,15; Р B = 3; Q A = 196; Q B = 80. Остальные результаты функционирования хозяйства приведены в табл. 7.1–7.4. Таблица 7.1 Равновесие на рынках благ
Таблица 7.2 Пример 7.1 Допустим, что отраслевые функции спроса и предложения двух взаимозаменяемых благ А и В имеют вид:
Вследствие частичной взаимозаменяемости благ при повышении цены одного из них растет спрос на другое благо. Поскольку при выпуске благ применяются одни и те же факторы производства, то в случае повышения цены одного из благ производители увеличивают его предложение за счет сокращения предложения другого блага. Приравняв друг к другу спрос и предложение на рынке блага А, найдем его равновесную цену, зависящую от цены блага В:
Уравнение (7.1) определяет цену, которая обеспечивает равенство объемов спроса и предложения на рынке блага А при любой цене блага В, в том числе и неравновесной. Все значения Р A, которые обеспечивают равновесие на рынке блага А при неравновесных значениях Р B, являются ценами частичного равновесия: на одном рынке равновесие, на другом нет. Так, если Р B = 25, то цена Р A = 8,4 + 0,6 × 25 = 23,4 уравнивает объемы спроса и предложения на рынке блага А:
хотя на рынке блага В существует дефицит:
Чтобы найти то значение Р A, которое соответствует совместному равновесию на обоих рынках, нужно предварительно определить множество цен частичного равновесия на рынке блага В. Она определяется из условия равновесия на этом рынке:
Решение системы уравнений (7.1) и (7.2) дает значения цен, обеспечивающих совместное равновесие на обоих рынках:
Проверим состояние рынков при этих ценах:
Наглядно процесс установления совместного равновесия на двух рассматриваемых рынках изображен на рис. 7.1.
Рис. 7.1. Устойчивое совместное равновесие на двух рынках Допустим, на рынке блага A объемы спроса и предложения совпали при Р A = 15. Тогда в соответствии с (7.2) на рынке блага В равновесие установится при 23,8. Но тогда по (7.1) для сбалансированности рынка блага А требуется Р A = 22,7. Через несколько шагов установится совместное равновесие при Р A = 26; Р B = 29,3. Рисунок 7.1 показывает, что совместное равновесие при заданных функциях спроса и предложения является устойчивым. Однако так бывает не всегда. Если бы спрос и предложения на рынках отображался следующими функциями:
то совместное равновесие на обоих рынках обеспечивали бы цены Р A = 2,7; Р B = 2. Но это неустойчивое равновесие, что иллюстрирует рис. 7.2. При определенных параметрах функций спроса и предложения прямые Р A(Р В) и Р В(Р A) вообще могут не пересечься в квадранте положительных цен; это означает, что совместного равновесия нс может быть. Если достижение совместного равновесия хотя бы только на двух рынках связано с выполнением целого ряда условий, то возможно ли существование общего экономического равновесия в экономике с множеством рынков благ и факторов производства? Для ответа на этот вопрос нужна модель, описывающая функционирование всего национального хозяйства. В ней кроме взаимодействия производителей и потребителей на рынках благ необходимо отразить взаимодействие между субъектами общественного хозяйства на рынках факторов производства, где формируются доходы потребителей, определяющие их спрос на блага. Первым экономистом, построившим такую модель, был Леон Вальрас[1].
Рис. 7.2. Неустойчивое совместное равновесие на двух рынках Общее экономическое равновесие (ОЭР). С включением в модель рынков факторов производства экономика предстает в виде замкнутой системы, схематически представленной на рис. 7.3.
Рис. 7.3. Взаимозависимость рынков благ и факторов производства На рынках благ домашние хозяйства осуществляют расходы, а фирмы получают доходы; на рынках факторов, наоборот, домашние хозяйства имеют доходы в виде заработной платы и дивидендов, а фирмы несут расходы по оплате труда и капитала. Предполагается, что экономические агенты не делают сбережений, т.е. все доходы расходуются на покупку благ и факторов производства. Так, если в экономике используются два фактора производства (L, К) и производятся два блага (Л, В), то для каждого экономического субъекта выполняется равенство
Равенство (7.3) означает, что расходы субъекта на покупку благ и факторов производства (левая часть) равны его доходам от продажи благ и предоставления услуг труда и капитала (правая часть). Представим его в другом виде:
В скобках представлен результат сделок экономического субъекта на каждом из рынков; их суммарный результат равен нулю. Сложив результаты сделок всех участников на всех рынках, получим следующее равенство:
Каждое из слагаемых правой части равенства (7.4) характеризует конъюнктуру на отдельном рынке: если оно равно нулю, то на рынке достигнуто равновесие; в противном случае на рынке существует дефицит или избыток. Из равенства (7.4) вытекают два важных свойства национальной экономики. Во-первых, при отсутствии общего экономического равновесия сумма избытков на одних рынках равна сумме дефицитов на других рынках. Во-вторых, если некоторая система цен обеспечивает равновесие на любых трех рынках (превращает в нуль разность в любых трех скобках), то равновесие будет и на четвертом рынке (нулю будет равна и разность в четвертой скобке). Этот вывод, верный для любого числа рынков, назван законом Вальраса. В соответствии с законом Вальраса система из п уравнений, представляющих условия равновесия на п взаимосвязанных рынках, содержит только п – 1 независимых уравнений и потому не имеет однозначного решения. Для преодоления этого препятствия необходимо либо добавить еще одно независимое уравнение, либо исключить одно неизвестное. Первый вариант используется в макроэкономике; в качестве дополнительного берется уравнение, определяющее равенство спроса и предложения на рынке денег. В микроэкономике применяется второй вариант. Для объяснения микроэкономических явлений достаточно знать систему относительных цен, которая основана на том, что определенное количество одного товара служит масштабом цен при измерении ценности всех других товаров. Цена избранного товара принимается за единицу и тогда число неизвестных оказывается равным числу независимых уравнений. Как известно из математики, само по себе такое равенство не гарантирует существования решения соответствующей системы уравнений, особенно если искомые переменные должны иметь положительные значения. В этом мы могли убедиться в предыдущем разделе данной главы. Однако К. Эрроу и Г. Дебре доказали, что модель Л. Вальраса имеет однозначное решение, если:
Пример 7.2 Экономика состоит из двух представительных домашних хозяйств, потребляющих два блага (А и В), и двух представительных фирм, одна из которых производит благо А, другая – благо В. Хозяйство ведется в условиях совершенной конкуренции, поэтому каждый из его участников воспринимает цены в качестве экзогенных параметров. Предпочтения домашних хозяйств относительно потребляемых благ и свободного времени отображаются следующими функциями полезности:
Бюджеты домашних хозяйств образуются из заработной платы и доходов от капитала. У первого домашнего хозяйства имеется К 1 = 40 капитала, а у второго – К 2 = 60. Поэтому бюджетные уравнения домашних хозяйств имеют вид:
Технология производства благ отображается функциями:
Таковы исходные данные. По ним, опираясь на изученное содержание предыдущих глав, нужно определить:
Приступим к решению этой задачи. Так как предпочтения потребителей отображаются функцией полезности Стоуна, то их функции спроса на блага и предложения труда выводятся так, как показано в Приложение к гл. 3; в роли блага С теперь выступает свободное время (280 -
Функции спроса фирм на труд и капитал выведены в параграфе 6.2. В рассматриваемом примере они получаются такими:
Подставив найденные величины в функцию средних затрат длительного периода
Средние затраты у обеих фирм оказались неизменными при любом выпуске из-за того, что их технологии имеют неизменную отдачу от масштаба. Следовательно, равновесные цены благ будут равны средним затратам:
Добавим к равенствам (7.5) условия равновесия на рынке капитала, труда и рынке блага А:
В соответствии с законом Вальраса при равновесии на этих трех рынках на рынке блага В тоже будет равновесие. В системах (7.5)-(7.8) – пять независимых уравнений с шестью неизвестными. Приняв w = 1, из решения системы получаем значения остальных пяти переменных: r = 2,26; Р A = 2,15; Р B = 3; Q A = 196; Q B = 80. Остальные результаты функционирования хозяйства приведены в табл. 7.1–7.4. Таблица 7.1 Равновесие на рынках благ
Таблица 7.2 13.2. 13.3. Эффективность в обмене Концепция экономической эффективности включает в себя экономику распределения, или обмена. Под эффективным распределением (обменом) благ понимается такое их распределение между потребителями, при котором невозможно распределить блага таким образом, чтобы благосостояние одного или нескольких потребителей улучшилось без ухудшения благосостояния другого или других. Иными словами, распределение (обмен) является Парето-эффективным, если блага нельзя перераспределить так, чтобы кому-то стало лучше, но никому - хуже. Анализ построим на следующих предположениях:
На рис. 13.3 Исходное распределение находится в точке А, через которую проходят кривые безразличия Обмен, начавшийся из точки А и передвигающий распределение благ за пределы заштрихованной части, ухудшает положение одного из потребителей, и потому он будет невозможен. Перемещение из А в В неэффективно, поскольку кривые Кривая контрактов иллюстрирует все распределения, после которых невозможны дальнейшие взаимовыгодные сделки между потребителями. Такие распределения называют Парето-эффективными. На рис. 13.4 показаны три Парето-эффективных распределения (Е, F, G), несмотря на то, что каждое включает различные наборы благ, при этом ни один из потребителей не может улучшить своего положения без ухудшения состояния другого. Указанные точки являются эффективными в распределении благ между потребителями, но они не равнозначны для них. Так, передвигаясь по контрактной линии от точки Е к точке F, мы улучшаем состояние одного потребителя, но ухудшаем состояние другого потребителя. На конкурентных рынках имеется много покупателей и продавцов. Это означает, что если потребителей не устраивают условия обмена, они могут найти других, которые предложат им лучшее, в результате чего формируется конкурентное равновесие. Конкурентное равновесие - это набор цен, при котором объем спроса равен объему предложения благ на каждом рынке. Итак, при конкурентном равновесии потребителей:
В условиях, когда имеется много потребителей и производителей, обеспечить эффективное распределение благ достаточно сложно. Это возможно в том случае, если на всех рынках существует совершенная конкуренция. Эффективное распределение возможно посредством распределения всех благ государственными органами, т.е. при централизованной системе. Однако конкурентное решение нередко предпочтительней благодаря минимуму требуемой информации, ибо все потребители должны знать только свои собственные предпочтения и цены. 13.4. Оптимальность по Парето Понятие «оптимальность по Парето» тесно связано с понятиями «Парето-предпочтительности» и «Парето-несравнимости» и может быть определено только во взаимной увязке. Парето-предпочтительным считается такое состояние экономики относительно другого ее состояния, когда в первом случае благосостояние хотя бы одного вида выше, а всех остальных не ниже, чем во втором случае. Понятие Парето-предпочтительности применимо только в тех случаях, когда та или иная пара точек в пространстве благосостоянии может быть соединена прямой с неотрицательным наклоном. Парето-несравнимость - это такое состояние экономики, когда любая точка, расположенная на границе возможных благосостоянии, несравнима в отношении любой другой точки на этой границе. Оптимальность по Парето гласит: «Следует считать, что любое изменение, которое никому не причиняет убытков и которое приносит людям пользу (по их собственной оценке), является улучшением». Оптимальное по Парето распределение и использование производственных ресурсов выступает необходимой предпосылкой для достижения эффективности производства. Оптимальность по Парето является одним из самых распространенных критериев оптимальности. Он предназначен для того, чтобы определить, улучшает ли предложенное изменение в экономике общий уровень благосостояния. В зарубежной экономической теории проблема достижения общественной эффективности распределения ресурсов разработана итальянским экономистом Вильфредо Парето (1848-1923). Согласно его концепции, общество находится в состоянии общего экономического равновесия и социальной эффективности распределения ресурсов, которое предполагает оптимальное распределение в сфере производства при минимальном использовании ресурсов и эффективное распределение в сфере потребления, которое обеспечивает максимум удовлетворения потребностей. Рыночная экономика в условиях совершенной конкуренции автоматически достигает оптимума по Парето. Оптимальность по Парето неприменима к ситуации, когда предложенное изменение приносит пользу одним, в то же время наносит потери другим. Имеется много различных оптимальных по Парето вариантов распределения ресурсов, при которых мера удовлетворения, достигаемая разными группами общества, может существенно отличаться. Экономическая теория не может определить, какое из оптимальных по Парето распределений ресурсов общества является наилучшим с социальной точки зрения. Выбор среди оптимальных вариантов применения ресурсов является проблемой социальной справедливости, требующей использования функции общественного благосостояния. Перемещение из одной точки эффективного по Парето распределения к другой такой же точке нередко предполагает государственное вмешательство в процесс перераспределения доходов и ресурсов общества. Выделяют три условия обеспечения оптимальности по Парето. Первое условие. Оптимальное распределение благ между потребителями исходит из соблюдения условия, согласно которому предельная норма замещения двух благ должна быть одинаковой для обоих потребителей. Предположим, что в экономике производятся два блага А и В, тогда:
Второе условие. Оптимальное распределение ресурсов в производстве. Для производства благ X и Y имеется два ресурса i и j. В этом варианте должно соблюдаться равенство, согласно которому соотношение предельных продуктов i и j используемых для производства блага X, равно соотношению предельных продуктов i и j в производстве блага Y, а именно:
Третье условие. Оптимальный объем производства. Граница производственных возможностей показывает количество благ X и Y, которые могут быть произведены в условиях полного использования ресурсов. Оптимальным объем производства для любых двух благ будет при соблюдении следующих соотношений:
Это значит, что отношение предельных издержек к предельной полезности должно быть одинаковым для обоих благ. 13.5. 13.6. Общественный выбор Общественный выбор означает выявление и согласование предпочтений индивидов в латентной группе. В теории конституционного выбора любое решение признается оптимальным по Парето, если оно принято единогласно. Но в этом случае затраты на выявление и согласование предпочтений очень высоки, что предполагает выявление оптимума между количеством индивидов в группе, чье согласие требуется для принятия решения, и затратами согласования предпочтений данных индивидов. Когда размер решающей подгруппы составляет лишь один индивид, к тому же заранее известный, то модель такой латентной группы называется диктатурой. Главная проблема общественного выбора - это проблема рационального поведения голосующих, и заключается в том, что, с позиции отдельного индивида нерационально осуществлять значительные старания с целью извлечения информации, способствующей более рациональному общественному выбору. Общественный выбор в условиях прямой и представительной демократии существенно различается. В условиях прямой демократии каждый член латентной группы лично голосует по любому вопросу; в условиях представительной демократии решения принимают либо особым образом избранные представители членов группы, либо депутаты. Представительная демократия имеет определенные достоинства, основным из которых является наличие возможности извлечения пользы из общественного разделения труда. Депутаты делают выбор более оптимально, поскольку специализируются на принятии решений. Однако при представительной демократии могут быть такие решения, которые не отвечают интересам даже простого большинства. Значительный вклад в теорию общественного выбора внесли американские экономисты, лауреаты Нобелевской премии по экономике Дж. Бьюкенен, К. Эрроу, индийский экономист А. Сен. Теорема К. Эрроу о невозможности. Американский экономист К. Эрроу в конце 40-х гг. XX в. сделал попытку исследовать проблему общественного выбора в более общем значении - существует ли способ трансформации индивидуальных предпочтений в коллективные. При этом Эрроу сформулировал предпосылки, при которых такое превращение возможно. Суть теоремы о невозможности заключается в том, что нельзя создать систему принятия коллективных решений, удовлетворяющую требованиям полной упорядоченности, транзитивности, универсальности, Парето-совместимости, отсутствия диктатуры, назависимости от других альтернатив. Этот вывод Эрроу в экономической литературе назван теоремой Эрроу о невозможности. Другими словами, общественный выбор нельзя признать в одно и то же время и рациональным, и не диктаторским. Теорема Эрроу не означает, что осуществление рациональных общественных решений в принципе невозможно. Речь в ней идет только об отсутствии гарантий рациональности. При одинаковых индивидуальных предпочтениях решение об общественном предпочтении не является сложным. В этой связи высказываются суждения об «единообразии» индивидуальных предпочтений посредством системы обязательного образования, регулируемой государством. Оппоненты теории о невозможности выступают против таких общих требований к общественным и индивидуальным предпочтениям, как полная упорядоченность и транзитивность, ибо каждый индивид имеет собственные интересы и предпочтения. Теорема о невозможности в течение долгого времени казалась неп
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2020-10-24; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.174.100 (0.016 с.) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

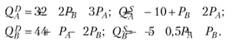
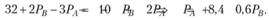 (7.1)
(7.1)

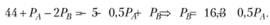 (7.2)
(7.2)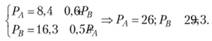


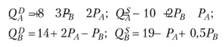
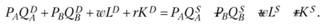 (7.3)
(7.3)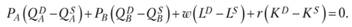
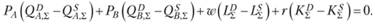 (7.4)
(7.4)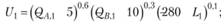
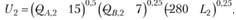
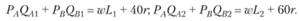
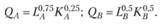
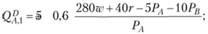
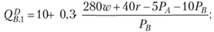

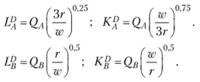
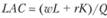 получим:
получим: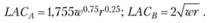
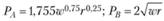 (7.5)
(7.5)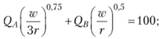 (7.6)
(7.6) (7.7)
(7.7) (7.8)
(7.8) изображена эффективность распределения товаров. График строится таким образом: вначале рисуют карту кривых безразличия для одного потребителя по двум товарам, затем переворачивают ее на 180
изображена эффективность распределения товаров. График строится таким образом: вначале рисуют карту кривых безразличия для одного потребителя по двум товарам, затем переворачивают ее на 180  и рисуют карту кривых безразличия для другого потребителя по тем же двум товарам. Кривые безразличия у обоих потребителей вогнутые, если смотреть на них с противоположных сторон. Для первого потребителя кривые безразличия отсчитываются от начала координат 0; для другого - с противоположного правого верхнего угла диаграммы.
и рисуют карту кривых безразличия для другого потребителя по тем же двум товарам. Кривые безразличия у обоих потребителей вогнутые, если смотреть на них с противоположных сторон. Для первого потребителя кривые безразличия отсчитываются от начала координат 0; для другого - с противоположного правого верхнего угла диаграммы.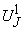 и
и 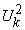 которые отражают MRS у обоих потребителей и соответствуют наклону кривых безразличия в точке А. Заштрихованная часть рисунка между этими кривыми безразличия соответствует всем возможным вариантам распределения благ, обеспечивающим двум потребителям более предпочтительное состояние, нежели в точке А.
которые отражают MRS у обоих потребителей и соответствуют наклону кривых безразличия в точке А. Заштрихованная часть рисунка между этими кривыми безразличия соответствует всем возможным вариантам распределения благ, обеспечивающим двум потребителям более предпочтительное состояние, нежели в точке А.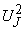 и
и 
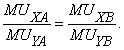
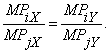
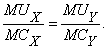
 Общественный выбор осуществляется путем голосования. Выделяют конституционный и постконституционный общественный выбор. Первый означает выбор правил «игры», второй - выбор в процессе игры установленных ограничений.
Общественный выбор осуществляется путем голосования. Выделяют конституционный и постконституционный общественный выбор. Первый означает выбор правил «игры», второй - выбор в процессе игры установленных ограничений.


