Какие переменные модели называются экзогенными, а какие — эндогенными.

 

Для описания основных видов элементов экономической модели рассмотрим конкретную ситуацию и построим соответствующую ей модель.

 

Пусть имеется фирма, выпускающая несколько видов продукции. В процессе производства используются три вида ресурсов: оборудование, рабочая сила и сырье; эти ресурсы однородны, количества их известны и в данном производственном цикле увеличены быть не могут. Задан расход каждого из ресурсов на производство единицы продукции каждого вида. Заданы цены продуктов. Нужно определить объемы производства с целью максимизации стоимости произведенной продукции (или, в предположении, что вся она найдет сбыт на рынке - общей выручки от реализации).

 

Для решения поставленной задачи нужно построить математическую модель, наполнить ее информацией, а затем провести по ней необходимые расчеты. Вначале при построении модели нужно определить индексы, экзогенные и эндогенные переменные и параметры. В нашей задаче свой индекс должен иметь каждый вид продукции (пусть это индекс i, меняющийся от 1 до n), а также вид ресурсов (если мы обозначаем их одной переменной; пусть в нашей задаче ресурсы обозначены разными переменными). Далее опишем экзогенные переменные - те, которые задаются вне модели, то есть известны заранее, и параметры - это коэффициенты уравнений модели. Часто экзогенные переменные и параметры в моделях не разделяют.

В рассматриваемой задаче заданы экзогенные переменные следующие:

 

имеющиеся количества оборудования К, рабочей силы L и сырья R;

 

заданы параметры - коэффициенты их расхода на единицу i-й продукции: ki, li и ri, соответственно. Цены продуктов pi также известны.

 

Далее вводятся обозначения для эндогенных переменных — тех, которые определяются в ходе расчетов по модели и не задаются в ней извне. В нашем случае - это неизвестные объемы производства продукции каждого i-го вида; обозначим их xi.

Закончив описание переменных и параметров, переходят к формализации условий задачи, к описанию ее допустимого множества и целевой функции (если таковая имеется). В нашей задаче допустимое множество - это совокупность всех вариантов производства, обеспеченных имеющимися ресурсами. Оно описывается с помощью системы неравенств:

 

k1x1 + k2x2 + … + knxn ≤ K,

l1x1 + l2x2 + … + lnxn ≤ L,

r1x1 + r2x2 + … + rnxn ≤ R.

 

К этим ограничениям по ресурсам добавляются требования неотрицательности переменных xi ≥ 0. Если бы какой-то ресурс нужно было израсходовать полностью (например, полностью занять всю рабочую силу), соответствующее неравенство превратилось бы в уравнение. Это сузило бы допустимое множество и, возможно, исключило бы из него первоначально наилучшее решение.

 

Если модель является оптимизационной (а данная модель такова), то наряду с ограничениями должна быть выписана целевая функция, т.е. максимизируемая или минимизируемая величина, отражающая интересы принимающего решение субъекта. Для данной задачи максимизируется величина

 

p1x1 + p2x2 + … + pnxn → max.

Поставленная задача далеко не всегда хорошо описывает ситуацию и соответствует задачам лица, принимающего решение (ЛПР).

 

В действительности, по крайней мере:

 

1) ресурсы до некоторой степени взаимозаменяемы;

 

2) затраты ресурсов не строго пропорциональны выпуску (есть постоянные затраты, не связанные с объемом выпуска; предельные затраты меняются);

 

3) объемы ресурсов не строго фиксированы, они могут покупаться и продаваться, браться или сдаваться в аренду;

 

4) внутри каждого вида ресурсов можно выделить составляющие, функционально или качественно различные, в той или иной мере заменяющие или дополняющие друг друга и по-разному влияющие на объем выпуска;

 

5) цена продукта может зависеть от объема его реализации, то же касается цены ресурса;

 

6) фирма может использовать одну из конечного набора технологий (или сочетание нескольких таких технологий), характеризующихся определенными сочетаниями используемых ресурсов;

 

7) различные единицы получаемой прибыли могут иметь разную ценность для лица, принимающего решение (что обусловлено, например, особенностями налоговой системы);

8) интересы и предпочтения субъекта не ограничиваются максимизацией объема прибыли, поэтому целевая функция должна учитывать и другие количественные и качественные показатели;

 

9) для субъекта реально решаемая задача не ограничивается одним моментом или периодом времени, важны динамические взаимосвязи;

 

10) на ситуацию могут воздействовать случайные факторы, которые необходимо принять во внимание.

 

Многие разделы экономической теории посвящены изучению, описанию и моделированию перечисленных аспектов на различных уровнях хозяйственной деятельности, с той или иной степенью детализации и в различных сочетаниях.

 

ПРИМЕР 3. (П ОСТРОЕНИ Е МАТЕМАТИЧЕСКОЙ МОДЕЛИ ЭКОНОМИЧЕСКОГО ОБЪЕКТА).

 

Рассмотрим пример экономико-математической модели задачи (о диете или рациональных смесях) формирования экономного суточного набора продуктов питания.

 

Введем следующие обозначения:

 

m — количество питательных веществ;

 

n — количество продуктов питания;

 

cj - цена 1 кг j-го продукта, руб.;

 

zj — запас j-го продукта, кг;

 

qi - i-е питательное вещество;

 

bi - норма суточной потребности в i-м питательном веществе, г;

qij - вес i-го питательного вещества в 1 кг j-продукта, г;

 

xj — вес j-го продукта в общем наборе питания, кг;

 

С - общие затраты на питание, руб.

 

Взаимосвязи между перечисленными показателями задачи формально можно записать в обобщенном виде таким образом:

 

С = f(cj, zj, qi, bi, qij, xj, m, n) → min,

 

или в виде математических уравнений, неравенств и систем уравнений, что в сочетании с содержательной частью задачи имеют следующий вариант постановки:

Найти оптимальные величины веса каждого продукта питания в общем наборе

 

x1=?, x2 =?, …, xn =?

 

при следующих ограничениях:

 

вес каждого питательного вещества в наборе должен быть более или равен суточной норме потребления человека:

 

qi1x1 + qi2x2 + … + qinxn ≥ bi, i = 1, …, m;

 

причем каждый продукт должен входить в диету и, кроме того, его вес не должен превышать величины имеющегося запаса:

 

0 < xj ≤ zj, j = 1, …, n;

 

а стоимость набора продуктов при этом должна быть наименьшей:

 

С= c1x1 + c2x2 + … + cnxn → min.

Записанные уравнения и неравенства — совокупность, которая представляет собой экономико-математическую модель задачи. Решение этой задачи можно получить с помощью, например, методов линейного программирования.

 

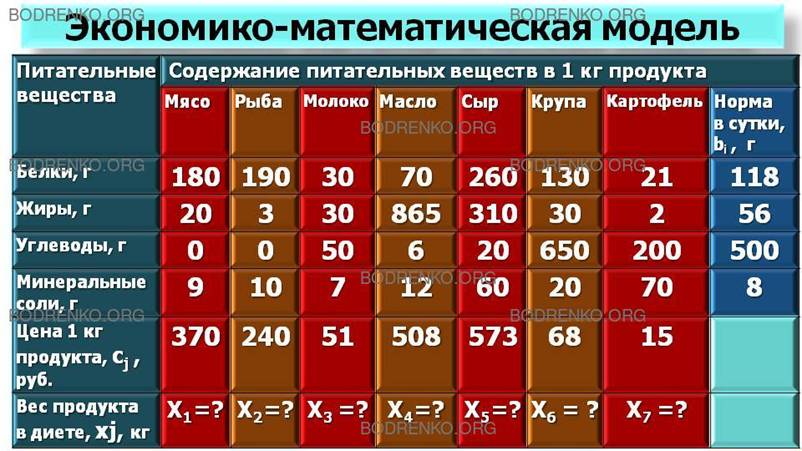
Экономико-математическую модель этой же задачи можно представить еще и в матричном виде. Например, для поддержания нормальной жизнедеятельности человеку ежедневно необходимо потреблять белки, жиры, углеводы, минеральные соли. Количество питательных веществ, содержащихся в 1 кг имеющихся продуктов питания, а также их стоимость и нормы суточной потребности питательных веществ изображены в виде матрицы (таблица 1).

 

Таблица 1.

 

Питательные вещества	Содержание питательных веществ в 1 кг продукта
	Мясо	Рыба	Молоко	Масло	Сыр	Крупа	Картофель	Норма в сутки, bi, г
Белки, г	180	190	30	70	260	130	21	118
Жиры, г	20	3	30	865	310	30	2	56
Углеводы, г	0	0	50	6	20	650	200	500
Минеральные соли, г	9	10	7	12	60	20	70	8
Цена 1 кг продукта, cj, руб.	370	240	51	508	573	68	15
Вес продукта в диете, xj, кг	X1=?	X2 =?	X3 =?	X4 =?	X5 =?	X6 =?	X7 =?

Требуется составить дневной рацион продуктов питания, содержащий не менее суточной нормы потребности человека в необходимых питательных веществах и обеспечивающий минимальную общую стоимость продуктов.

 

Экономико-математическая формулировка и модель этой задачи имеют следующий вид:

 

Найти оптимальный вес имеющихся продуктов питания при ограничениях, связанных с суточной нормой потребления, записанных в виде системы неравенств:

 

180x1 +190x2 +30x3 +70x4+260x5 +130x6 +21x7 ≥ 118,

 

20x1 +3x2 +40хз +865x4 +310x5 +30х6 +2x7 ≥ 56,

 

0x1 + 0x2 +50хз +6x4 +20x5 +650x6 +200x7 ≥ 500,

 

9x1 +10x2 +7x3 +12x4 +60x5 +20х6 +70x7 ≥ 8,

 

x1 > 0, x2 > 0, x3 > 0, x4 > 0, x5 > 0, x6 > 0, x7 > 0;

 

решение которой позволяет определить минимум затрат на продукты питания:

 

С= (370x1 + 240x2 + 51x3 + 508x4 + 573x5 + 68х6 + 15x7) → min.

Дальнейшим развитием задачи о рациональном питании являются постановки и решения задач, связанных с товароснабжением и управлением товарными запасами на коммерческих предприятиях. Задача управления товарными запасами связана с поиском ответов на следующие вопросы: кому, когда и в каком объеме заказывать товары; какой лучший маршрут перевозки товаров; каким транспортом перевозить: автомобильным, железнодорожным или воздушным; какая частота и величина поставок товара?

 

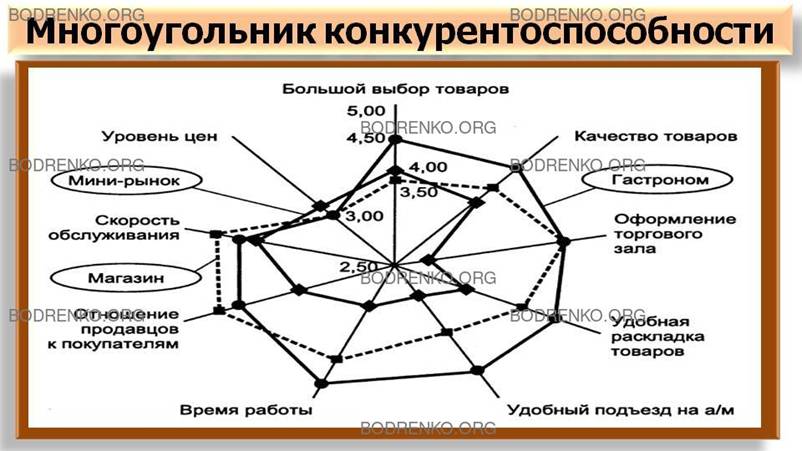
Интересной моделью является многоугольник конкурентоспособности (рисунок 1), показывающий соотношение различных показателей на плоскости, иногда его называют радаром или полигоном по аналогии с экраном радиолокатора. По каждой оси для отображения уровня значений каждого из исследуемых факторов используется определенный масштаб измерений, часто в виде балльных оценок. Изображая на одном рисунке многоугольники конкурентоспособности для разных предприятий, можно провести анализ уровня их конкурентоспособности по разным факторам.

 

Рисунок 1. Многоугольник конкурентоспособности.

 

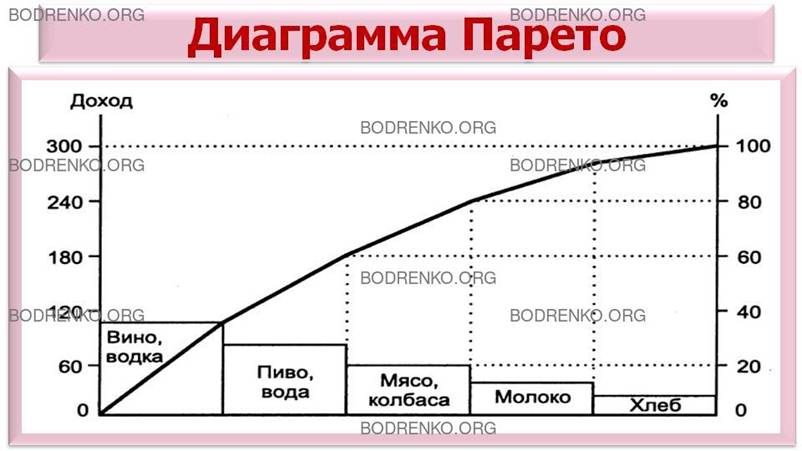
Для выявления наиболее вероятных или проблемных задач, на которых следует сосредоточить усилия фирмы, необходимо сравнить несколько факторов, влияющих на интересующий показатель коммерческой деятельности. Для этого можно использовать диаграммы относительной важности, получаемые, например, методами экспертных оценок. Графики такого вида (рисунок 2) называют диаграммами Парето, по имени итальянского экономиста.

Рисунок 2. Диаграмма Парето.