
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямые методы решения СЛАУ. Метод прогонки.Содержание книги Поиск на нашем сайте Прямыми называют такие методы, которые используют конечные соотношения (формулы) для выполнения заранее известного числа операций. При этом, если исходные данные точны, то результат будет точным, поэтому прямые методы называют точными методами. Но исходные данные обычно не точны и при решении задачи прямыми методами происходит накопление погрешностей. Чем больше число уравнений, тем больше погрешностей, поэтому прямые методы используют, если n<200. К прямым методам относятся, формулы Крамера, метод Гауса, метод Жордана и метод прогонки. Метод прогонки применяется для решения систем уравнений с трехдиагональной (ленточной) матрицей. Такая система уравнений записывается в виде:
Является частным случаем метода Гаусса и состоит из прямого и обратного хода. Прямой ход состоит в исключении элементов матрицы системы (2.6), лежащих ниже главной диагонали. В каждом уравнении останется не более двух неизвестных и формулу обратного хода можно записать в следующем виде:
Уменьшим в формуле (2.7) индекс на единицу:
Выразим
Сравнивая (2.7) и (2.8), получим:
Поскольку Теперь по формулам (2.9) и (2.10) можно вычислить прогоночные коэффициенты Итерационные методы решения СЛАУ. (метод Якоби) Суть вычислений итерационными методами состоит в следующем: расчет начинается с некоторого заранее выбранного приближения
Затем процесс повторяется, только вместо
При выполнении некоторых заранее оговоренных условий процесс сходится при
Заданная точность достигается при выполнении условия:
(метод Зейделя) Вычисления в этом методе почти такие же, как и в методе Якоби, с той лишь разницей, что в последнем новые значения
Сходимость и точность достигаются условиями (2.13) и (2.14). Методы простой итерации и Зейделя для решения систем нелинейных уравнений.
|
||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

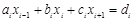
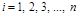
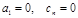 .
.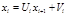 ,
, 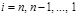 (2.7)
(2.7)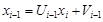 и подставим в (2.6):
и подставим в (2.6):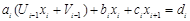
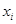 :
: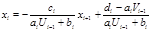 (2.8)
(2.8)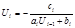
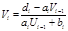
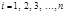 (2.9)
(2.9)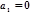 , то
, то 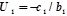 ;
; 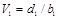 (2.10)
(2.10)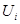 и
и 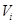 (
(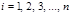 ). Это прямой ход прогонки. Зная прогоночные коэффициенты, по формулам (2.7), можно вычислить все
). Это прямой ход прогонки. Зная прогоночные коэффициенты, по формулам (2.7), можно вычислить все 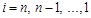 ) (обратный ход прогонки). Поскольку
) (обратный ход прогонки). Поскольку 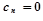 , то
, то 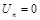 и
и 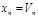 . Далее вычисляем
. Далее вычисляем 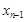 ,
, 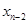 ,...,
,..., 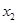 ,
, 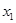 .
.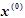 (начального приближения). Вычислительный процесс, использующий матрицу
(начального приближения). Вычислительный процесс, использующий матрицу 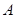 , вектор
, вектор 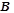 системы (2.1) и
системы (2.1) и 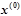 , приводит к новому вектору
, приводит к новому вектору 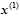 :
: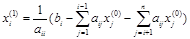 ,
, 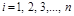 (2.11)
(2.11)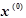 используется новое значение
используется новое значение 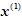 . На
. На 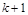 -м шаге итерационного процесса по получают:
-м шаге итерационного процесса по получают: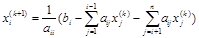 ,
, 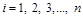 (2.12)
(2.12)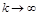 . Сходимость метода простой итерации обеспечивается при выполнении условия преобладания диагональных элементов матрицы A, т.е. при:
. Сходимость метода простой итерации обеспечивается при выполнении условия преобладания диагональных элементов матрицы A, т.е. при: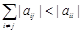 ,
, 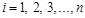 (2.13)
(2.13)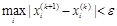 (2.14)
(2.14)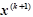 не используются до новой итерации. В методе Зейделя при нахождении
не используются до новой итерации. В методе Зейделя при нахождении 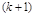 -ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой:
-ой компоненты используются уже найденные компоненты этой же итерации с меньшими номерами, т.е. последовательность итераций задается формулой: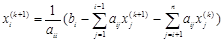 ,
, 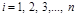 (2.17)
(2.17)


