
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Численные методы. Погрешность вычислений.Содержание книги Поиск на нашем сайте Основным инструментом для решения сложных математических задач в настоящее время являются численные методы, позволяющие свести решение задачи к выполнению конечного числа арифметических действий над числами. При этом результат получается в виде числовых значений. Обычно результат находится с некоторой погрешностью. Есть четыре источника погрешности результата: 1) математическая модель, 2) исходные данные, 3) численный метод, 4) округление при вычислениях. Погрешность математической модели связана с тем, что она охватывает важнейшие для данной задачи стороны явления, но не все. Исходные данные не точны, т.к. они являются результатами измерений или эксперимента. Погрешность исходных данных называется неустранимой погрешностью т.к. не зависит от исследователя. Погрешность метода связана с тем, что решение задачи сформулированной в терминах более сложных (производные, интегралы, диф. уравнения), сводится к вычислению в определённом порядке арифметических выражений. 36) Метод деления отрезка пополам для решения уравнений вида f(x)=0. Пусть найден интервал [a, b], на концах которого функция f (x) имеет разные знаки, т.е. f(a)f(b)<0. Это означает, что на интервале [a, b] содержится несколько корней уравнения. Если интервал достаточно короткий, то корень один. Интервал [a,b] делим на два: x = (a+b)/2 и получим 2 интервала [a,x], [x,b]. Из двух интервалов выбираем тот, на концах которого функция имеет разные знаки, ибо этот интервал содержит корни. Выбранный интервал снова делим пополам, и из двух интервалов выбираем тот, на концах которого функция имеет разные знаки, либо этот интервал содержит корни и т.д. Если требуется найти корень с точностью ε, то деление продолжаем до тех пор, пока длина интервала не станет меньше ε, после этого любое число из этого интервала можно взять в качестве значения корня, вычисленного с точностью ε. Алгоритм метода деления отрезка пополам. Если f(a)f(х)<0, то выбираем: иначе: Если (b-a)>ε, то: Если (b-a)<ε, то печатаем х. Конец. Программа (исходные данные: f(x), a, b, ε): DEF FNF(X) = f(x) NPUT a, b, eps 2 x=(a+b)/2 IF FNF(a)*FNF(x)<0 THEN b=x ELSE a=x IF (b-a)>ε THEN 2 PRINT x, FNF(x) END. 37) Метод решения нелинейных уравнений f(x)=0. Метод Ньютона. Если известно хорошее начальное приближение решения уравнения f(x) = 0, то эффективным методом повышения точности является метод Ньютона (метод касательных). Сформулируем достаточное условие сходимости метода. Пусть функция f(x) определена и дважды дифференцируема на интервале от a до b, причём должно быть f(a)f(b)<0, а производные f'(x) и f''(x) сохраняют знак на интервале от a до b. Тогда, исходя из начального приближения, Хо принадлежащие [a, b] и удовлетворяющих условию f(Хо) f"(Хо)>0, можно построить последовательность: Хк+1 = Хк - (f(Хк) / f'(Хк)), К=0,1,2,3…, сходящуюся к единственному на интервале [a, b] корню уравнения f(x)=0. Метод Ньютона позволяет (допускает) простую геометрическую интерпретацию. Выберем начальное приближение: f(b)>0, f''(b)>0 (т.к. функция вогнута) и Xo=b. К точке кривой с абсциссой X0 проведём касательную. Точку пересечения касательной с осью абсцисс обозначим Х1,к точке с абсциссой X1 снова проведем касательную, точку ее пересечения сосью обозначим X2 и т.д. Таким образом будем продвигаться все ближе к точке С, пока расстояние до него не станет меньше ε. Получим условие остановки: |Xk+1-C| < |Хк+1-Хк|< ε. Выведем расчетные формулы метода. У нас ABC - прямоугольный треугольник. tgα = ВС/АС tgα = f'(x) BC = (Xo) AC = Xo-X Уравнение касательной: Программа (исходные данные: f(X),f'(X), Xo, ε) DEF FNF (X)=f(x) DEF FNP (X)=f'(x) INPUT X, eps 2 Y=X - FNF(X)/FNP(X) IF ABS(Y-X)<eps THEN 5 X=Y: GOTO 2 5 PRINT Y,FNF (Y) END. 38) Метод простой итерации для решения уравнений вида f(x) =0 Для использования этого метода исходное нелинейное уравнение В качестве
Если известно начальное приближение корня Далее подставляя каждый раз новое значение корня в уравнение
Итерационный процесс прекращается, если результаты двух последовательных итераций близки, т.е.
|
||
|
Последнее изменение этой страницы: 2020-03-27; просмотров: 111; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.21 (0.008 с.) |

 необходимо привести к виду
необходимо привести к виду  .
. можно принять функцию
можно принять функцию  , где М‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации
, где М‑ неизвестная постоянная величина, которая определяется из условия сходимости метода простой итерации  . При этом для определения M условие сходимости записывается в следующем виде:
. При этом для определения M условие сходимости записывается в следующем виде: или
или 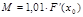 .
.  , подставляя это значение в правую часть уравнения
, подставляя это значение в правую часть уравнения  , получаем новое приближение
, получаем новое приближение 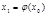 .
. , получаем последовательность значений:
, получаем последовательность значений: ,
,  ,...,
,..., 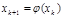 , k = 1,2,...,n.
, k = 1,2,...,n. .
.


