Передаточные функции цифровых алгоритмов

В дискретных системах с программной реализацией алгоритмов управления используются методы цифрового интегрирования. При этом передаточная функция алгоритма управления зависит от метода численного интегрирования и формы экстраполирования. Чаще всего используются методы прямоугольников, трапеций и Симпсона, которые содержат минимальное арифметических операций в алгоритме реализации, а в качестве фиксирующего звена используют фиксатор нулевого порядка.

Программную реализацию алгоритмов управления называют дискретной коррекцией. Каждой дискретной передаточной функции соответствует определенный алгоритм и наоборот.

Рассмотрим дискретную систему (рис. 9).

 

Рис. 9

 

Данную схему можно представить в виде (рис. 10)

 

 

 

Рис. 10

 

Допустим, задан алгоритм функционирования ЦА (рис. 11)

 

 

Рис. 11

 

x_вых[kT] = x_вых[kT-T]+x_вх[kT-T]. (11)

 

В соответствии с разностным уравнением, запишем операторное уравнение в форме z – преобразования:

x_вых(z) = z ^-1 x_вых(z) + z ^-1x_вх(z). (12)

 

При этом передаточная функция цифрового алгоритма имеет вид:

 

 (13)

 

Алгоритмы цифрового интегрирования

 

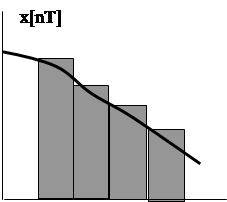
Передаточная функция алгоритма интегрирования по методу прямоугольников зависит от выбранного метода прямоугольной аппроксимации сигнала (рис. 12а, б).

В соответствии с рис. 12а, можно записать уравнение

 

y[kT]=y [kT-T]+x[kT] T, (14)

 

где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;

x[kT] T – приращение.

При этом передаточная функция алгоритма имеет вид

 

 (15)

 

В соответствии с рис 12б, можно записать уравнение

 

y[kT]=y [kT-T]+x [kT-T] T, (16)

 

где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;

x [kT-T] T – приращение.

При этом передаточная функция алгоритма имеет вид

 

 (17)

 

 

 

			0                        kT-T kT nT                     б)

Рис. 12

Интегрирование по методу трапеций

 

При интегрировании по методу трапеций (рис 13) можно записать уравнение

y[kT]=y [kT-T]+(x [kT-T]+x[kT]) T/2, (18)

 

где y[kT], y [kT-T] – текущее и предыдущее значение интеграла;

(x [kT-T]+x[kT]) T/2 – приращение.

 

Применив z – преобразование к уравнению (18), получим выражение для передаточной функции при трапецеидальной аппроксимации входного сигнала.

 

. (19)

 

 

Литература

 

1. Бронштейн И.Н., Семендяев К.Н. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986.

2. Дорф Р., Бишоп Р. Автоматика. Современные системы управления. 2002 г. – 832 с.

3. Харазов В.Г. Интегрированные системы управления технологическими процессами: Справочник. Издательство: ПРОФЕССИЯ, ИЗДАТЕЛЬСТВО, 2009. – 550 с.

4. Чебурахин И. Синтез дискретных управляющих систем и математическое моделирование: теория, алгоритмы, программы. Изд-во: НИЦ РХД, ФИЗМАТЛИТ, 2004. – 248c.