
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Прямой метод оценки динамического взаимодействия колеса транспортного средства и неровностей дорожного покрытия
(методика И.М.Рабиновича) 6.4.1 Теоретические исследования вертикального динамического воздействия транспортных средств на автомобильную дорогу, представленные в работах Бируля А.К. и Смирнова А.В. показали, что при увеличении скорости движения наблюдается рост динамической составляющей воздействия, которая увеличивается с увеличением высоты неровности дорожного покрытия. При этом величина динамического воздействия увеличивается и может в два и более раз превысить статическую нагрузку от транспортного средства. Амплитуды колебаний и их частотный диапазон зависят не только от высоты неровностей, а также от формы и длины.
Рисунок 6.3 Расчет коэффициента динамичности на участке автомобильной дороги Для различных микропрофилей поверхности автомобильных дорог в зависимости от преобладающих длин неровностей при различных скоростных режимах может наблюдаться значительное увеличение динамичности воздействия транспортного средства на конструкцию автомобильной дороги. 6.4.2 В качестве информативного параметра оценки динамического воздействия рекомендуется использовать вертикальное ускорение колебаний колеса транспортного средства. Согласно методики И.М.Рабиновича определяется вертикальное ускорение оси колеса транспортного средства при его взаимодействии с накопленной неровностью с учетом радиуса колеса, скорости транспортного средства и геометрии неровностей. Рассматриваются этапы взаимодействия колеса транспортного средства с радиальной поверхностью накопленной неровности (1), с входом и сходом с нее (2) [14]. 1. На рисунке 6.4 схематически изображены: профиль сечения неровности, ограниченный кривой Переход от горизонтального участка к криволинейному совершается резко, т.е. в этой точке траектория имеет две различные касательные. Плавный переход имел бы место, если бы между неровностью и дорожным покрытием была плавная переходная кривая, имеющая радиус кривизны, больший радиуса
Рисунок 6.4 Схема взаимодействия колеса транспортного средства
и накопленной неровности дорожного покрытия
Координаты произвольной точки
где Зная уравнение кривой Чтобы найти вертикальное ускорение центра колеса, соответствующее любому моменту качения по поверхности неровности (но не моменту вступления на нее или схода с нее), его выражают в функции от радиусов кривизны колеса и поверхности неровности. Первый обозначен как Рассматривается кривая
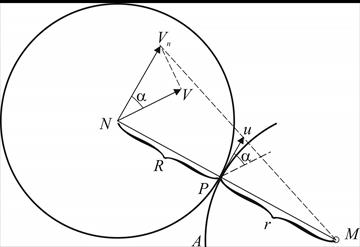
Рисунок 6.5 Расчетная схема Угловая скорость
Отрицательный знак перед дробью показывает, что в восходящей части траектории, где Вектор
Ускорение точки
Ускорение любой точки
На рисунке 6.7 показаны три составляющие ускорения точки Проекция суммарного ускорения точки
Формула представляет решение вопроса о вертикальных ускорениях центра колеса, получаемых во время качения по накопленной неровности. Вертикальное ускорение
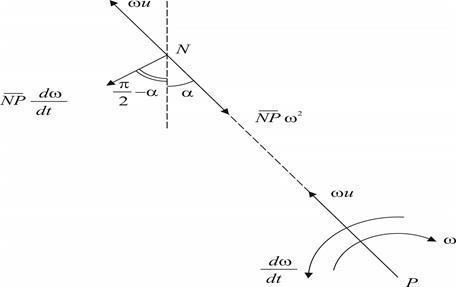
Рисунок 6.6 Расчетная схема
При восходящем и при нисходящем движении колеса ускорение направлено вниз, а сила инерции – вверх; весь период качения колеса по поверхности неровности есть период облегченного давления колеса на накопленную неровность. Ускорение и сила инерции, по мере движения колеса изменяются обратно пропорционально величине Радиусы кривизны колеса При данном радиусе При данном радиусе колес Формула (6.22) остается справедливой и при наличии переходной кривой от профиля неровности к дорожному покрытию. Переходная кривая имеет смысл в том случае, если по абсолютной величине ее радиус кривизны Во время движения по переходной кривой ускорение направлено вверх, а давление колеса при этом превышает статическое. При переходе через точку касания обеих кривых, несмотря на плавный характер их взаимного примыкания, ускорение, а вместе с ним и сила инерции, сразу меняют свой знак на обратный. Плавность перехода не устраняет удара. Формула (6.22) представляет решение вопроса и для движения колеса в углублении или впадине пути. 2. Также рассматриваются начальный и конечный моменты, т. е. припод-нимание колеса с дорожного покрытия, когда оно встречается с накопленной неровностью, и вступление на покрытие, когда покидает неровность. При соблюдении вышеуказанных условий (абсолютной жесткости дорожного покрытия, а также неровности и колеса) ускорение в оба эти момента направлено вверх и равно ∞. Сила инерции также равна ∞. Оба эти момента времени имеют малую продолжительность. Здесь имеется два удара, направленных вниз.
Второй случай можно привести к виду удара груза Получено:
Из этой формулы видно, что величина удара пропорциональна квадрату скорости и зависит от отношения между суммой радиусов кривизны и высотой
Зависимость При данных размерах препятствия (т.е. размерах 6.4.3 Разработан программный модуль имитационного моделирования процесса динамического взаимодействия колеса транспортного средства и дорожного покрытия с единичными и накопленными неровностями в среде МАТЛАБ. Результаты работы программного комплекса (типовые примеры) приве-дены на рисунке приложения 2 (представлены скриншоты изображений). 6.4.4 Достоинством предложенной методики является возможность получать численные ряды ускорений для сочетаний неровностей в виде коротких, средних и длинных волн. 6.4.5 Методика И.П.Рабиновича показывает нелинейный характер изменения вертикальных ускорений колеса по отношению к скорости транспортного средства, что будет учтено в формуле 6.30 (корреляционной зависимости взаимовлияния изменения коэффициента ровности IRI и изменения коэффициента динамичности с учетом квадратного корня скорости транспортного средства).
|
|||||||||||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 215; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.63.87 (0.015 с.) |

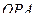 , и траектория
, и траектория 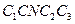 центра
центра  колеса. На участках
колеса. На участках 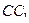 и
и 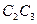 эта траектория имеет вид горизонтальной прямой, на участке
эта траектория имеет вид горизонтальной прямой, на участке 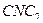 представляет собою кривую, эквидистантную кривой
представляет собою кривую, эквидистантную кривой 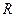 , где
, где 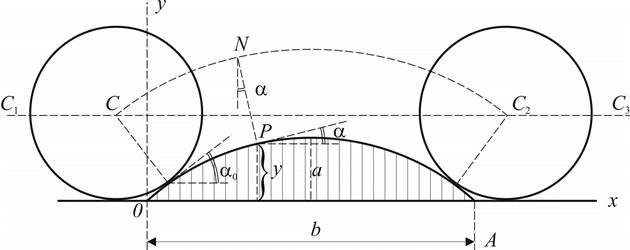
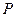 поверхности неровности обозначаются x, y. Центр
поверхности неровности обозначаются x, y. Центр 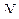 , характеризуемое координатами:
, характеризуемое координатами: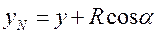 ,
, 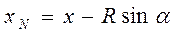 , (6.17)
, (6.17)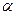 - угол наклона касательной в точке
- угол наклона касательной в точке 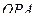 - накопленной неровности) как r. Величина
- накопленной неровности) как r. Величина 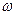 и угловое ускорение
и угловое ускорение 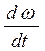 колеса:
колеса: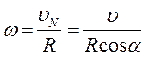 , (6.18)
, (6.18)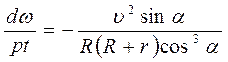 . (6.19)
. (6.19)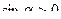 , угловое ускорение – отрицательно, т.е. направлено в сторону, противоположную направлению угловой скорости
, угловое ускорение – отрицательно, т.е. направлено в сторону, противоположную направлению угловой скорости  есть скорость точки
есть скорость точки 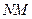 , вращающейся около точки
, вращающейся около точки 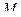 (центра кривизны неподвижной полодии в точке
(центра кривизны неподвижной полодии в точке 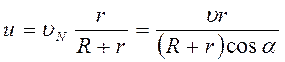 . (6.20)
. (6.20)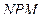 от точки
от точки 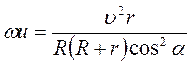 . (6.21)
. (6.21)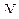 неизменяемой плоской системы, движущейся в своей плоскости представляется в виде геометрической суммы ускорения точки
неизменяемой плоской системы, движущейся в своей плоскости представляется в виде геометрической суммы ускорения точки 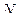 на вертикаль будет равна:
на вертикаль будет равна: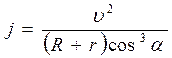 . (6.22)
. (6.22)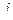 , выведенное при условии, что колесо катится по выпуклому контуру, направлено вниз. Так как угол
, выведенное при условии, что колесо катится по выпуклому контуру, направлено вниз. Так как угол 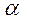 невелик и заклю-чен между пределами
невелик и заклю-чен между пределами 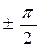 , то знак
, то знак 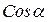 сохраняется на всем контуре.
сохраняется на всем контуре.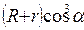 . Если сечение неровности представляет собой сечение круга, то ускорение уменьшается по закону
. Если сечение неровности представляет собой сечение круга, то ускорение уменьшается по закону 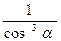 до достижения высшей точки траектории; где достигает своего минимума. Во время нисходящего движения колеса ускорение увеличивается по тому же закону. Ни в какой точке оно не равно нулю.
до достижения высшей точки траектории; где достигает своего минимума. Во время нисходящего движения колеса ускорение увеличивается по тому же закону. Ни в какой точке оно не равно нулю.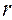 не играют роли каждый в отдельности; величина ускорения зависит лишь от их суммы. Большое колесо, катящееся по профилю большой кривизны (малого радиуса), и малое колесо, катящееся по профилю малой кривизны, дают один и тот же эффект, если только в обоих случаях сумма
не играют роли каждый в отдельности; величина ускорения зависит лишь от их суммы. Большое колесо, катящееся по профилю большой кривизны (малого радиуса), и малое колесо, катящееся по профилю малой кривизны, дают один и тот же эффект, если только в обоих случаях сумма 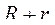 - одна и та же.
- одна и та же.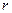 сила инерции будет тем меньше, чем больше будет радиус кривизны
сила инерции будет тем меньше, чем больше будет радиус кривизны 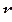 . Для этапа взаимодействия колеса транспортного средства с радиальной поверхностью накопленной неровности высота препятствия сама по себе не играет никакой роли; важна лишь кривизна его поверхности.
. Для этапа взаимодействия колеса транспортного средства с радиальной поверхностью накопленной неровности высота препятствия сама по себе не играет никакой роли; важна лишь кривизна его поверхности.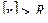 ; в противном случае колесо не сможет катиться по ней. Так как она обращена выпуклостью в обратную сторону (т. е. по направлению к настилу), то
; в противном случае колесо не сможет катиться по ней. Так как она обращена выпуклостью в обратную сторону (т. е. по направлению к настилу), то 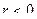 .
. , падающего с высоты
, падающего с высоты  . Формулы представлены в общем виде и годятся при любом выпуклом очертании поверхности накопленной неровности. В случае кругового очертания сечения неровности можно выразить угол
. Формулы представлены в общем виде и годятся при любом выпуклом очертании поверхности накопленной неровности. В случае кругового очертания сечения неровности можно выразить угол  в функции от основных размеров.
в функции от основных размеров.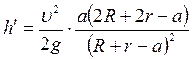 . (6.23)
. (6.23)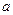 препятствия. Если обозначить
препятствия. Если обозначить 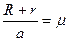 , то формула (6.33) будет упрощена:
, то формула (6.33) будет упрощена: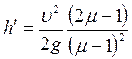 . (6.24)
. (6.24)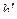 от
от 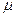 имеет гиперболический вид. При увеличении
имеет гиперболический вид. При увеличении 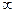 величина
величина 


