
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Билет 3. Измерение количества информации.Содержание книги
Поиск на нашем сайте
Информация для человека это содержание сигналов, воспринимаемых человеком непосредственно или с помощью различных устройств, расширяющая его знание об окружающем мире и протекающих в нем процессов. Существует два способа измерения информации: алфавитный и вероятностный. Алфавитный подход (набор знаков какого-либо языка) Каждый символ некоторого сообщения имеет определенный информационный вес – несет фиксированное количество информации. Все символы одного алфавита имеют один и тот же вес, зависящий от мощности алфавита. Информационный вес символа произвольного алфавита 1.Алфавит любого языка можно заменить двоичным алфавитом (он является универсальным). 2.Для кодировки N символов произвольного алфавита требуется i – разрядный двоичный код 3.Информационный вес символа = разрядность двоичного кода 4.Мощность алфавита и информационный вес символа алфавита: N = 2 i Единицы измерения информации 1 байт – информационный вес символа мощностью 256 1 байт = 8 битов= 1 Кб(килобайт) = 1024 байта = 1Мб(мегабайт) = 1024 Кб= 1Гб(гигабайт) = 1024 Мб= 1Тб(терабайт) = 1024 Гб= 1Пб(петабайт) = 1024 Тб=
Билет 4.Системы счисления. Система счисления – это знаковая система, в которой приняты определенные правила записи числа. Цифры - знаки,при помощи которых записываются числа. Алфавит - системы счисления- совокупность цифр. Системы счисления: Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависят от её положения в записи числа. Пример - римская система счисления. Каждый знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него. Система счисления называется позиционной, если количественный эквивалент цифры в числе зависит от её положения в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит. Двоичная система счисления. Двоичная СС- позиционная система счисления с основанием 2. Для записи чисел используются 2 цифры: 0 и 1. Чтобы перевести двоичное число в десятичное, необходимо вычислить сумму степеней двойки, соответствующих единицам в свернутой форме записи двоичного числа. Восьмеричная система счисления. Основание: 8. Для записи чисел используются цифры: 0,1,2,3,4,5,6,7. Для перевода целого восьмеричного числа в десятичное необходимо перейти к его развернутой записи и вычислить значение получившегося выражения. Для перевода целого десятичного числа в восьмеричную СС следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю.
Шестнадцатеричная система счисления. Основание: 16. Алфавит:0,1,2,3,4,5,6,7,8,9,A, B, C, D, E F. Правило перевода целых десятичных чисел в СС с основанием q 1)Последовательно выполнять деление данного числа и получаемых целых частных на основание новой СС до тех пор, пока не получим частное, равное нулю. 2)Полученные остатки, являющиеся цифрами числа в новой СС, привести в соответствие с алфавитом новой СС. 3)Составить число в новой СС, записывая его, начиная с последнего полученного остатка. «Компьютерные» СС В компьютерной технике используется двоичная СС, т.к. двоичные числа представляются в компьютере с помощью простых элементов с двумя устойчивыми состояниями, которые надежны и помехоустойчивы. Узловые и алгоритмические числа. Узловые числа обозначаются цифрами. Алгоритмические числа получаются в результате каких-либо операций из узловых чисел. Основная формула В позиционной системе счисления с основанием q любое число может быть представлено в виде A= ±( А-число, q- основание СС,
|
||||
|
Последнее изменение этой страницы: 2019-12-25; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.28 (0.006 с.) |

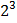 бит
бит байт =
байт =  бит
бит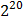 байт =
байт =  бит
бит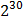 байт =
байт =  бит
бит байт =
байт =  бит
бит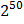 байт =
байт = 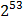 бит
бит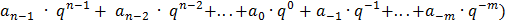
 - цифры алфавита данной системы, n-количество целых разрядов числа, m- количество дробных разрядов числа. Такая запись числа называется развернутой формой записи.
- цифры алфавита данной системы, n-количество целых разрядов числа, m- количество дробных разрядов числа. Такая запись числа называется развернутой формой записи.


