Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение конкурентоспособности с использованием функции желательностиСодержание книги
Поиск на нашем сайте
Использование функции желательности f для определения конкуренто-способности товара предложено Гончаровой Н.П.[9] Функция желательности определяется следующим образом:
где е — основание натурального логарифма; х — приведенное значение исследуемого параметра объекта. Функция определена в интервале 0...1 и используется в качестве безразмерной шкалы, названной шкалой желательности, для оценки уровней параметров сравниваемых объектов (изделий). С помощью шкалы желательности оцениваются параметры объектов или изделий с точки зрения их пригодности к использованию, или желательности, по отношению к какому-либо практическому применению. Каждому фактическому значению функции желательности придается конкретный экономический смысл, связанный с уровнем конкурентоспособности исследуемого объекта или изделия. Причем значение функции желательности, равное 0, соответствует неприемлемому уровню параметра, при значении которого изделие непригодно для выполнения стоящих перед ним задач; значение функции желательности, равное 1,00, соответствует полностью приемлемому уровню параметра, либо такому значению параметра, при котором дальнейшее улучшение нецелесообразно или невозможно. Промежуточные значения функции желательности, их экономическая характеристика приведены в табл. 1. Для выполнения дальнейших расчетов и графических построений необходимо получить значения приведенного параметра изделия, соответствующие узловым точкам шкалы желательности (табл. 1). Из формулы, приведенной выше, определим нужное значение. С этой целью прологарифмируем обе части уравнения:
(10)
Повторное логарифмирование позволяет получить следующую зависимость: x = –ln [–ln f ]. (12) С целью обеспечения возможности использования функции желательности для оценки параметров различной размерности и порядка производится приведение параметров изделия р к значениям приведенного параметра x функции желательности f. Для этого по известным значениям x и р на границах интервалов функции желательности строится аппроксимирующая функция и определяются ее параметры (коэффициенты). Наиболее простая — это линейная функция вида х = a х р + b, (13) где a, b — коэффициенты аппроксимации.
Таблица 2. Параметры функции желательности
Процедура получения оценки уровня параметра изделия по шкале (функции) желательности f включает следующие этапы: а) определение значений приведенного параметра х, соответствующих узловым точкам шкалы желательности f; б) определение значений параметра p, соответствующих границам интервалов шкалы желательности f (согласно условиям (критериям), приведенным в табл. 1); в) определение коэффициентов аппроксимации по данным х и р; г) вычисление значения x для конкретного значения оцениваемого параметра p; д) определение значения функции желательности f для оцениваемого параметра. Очевидно, что результаты сравнительной оценки конкурентоспособности различных изделий-аналогов будут в значительной степени зависеть от того, какие конкретные значения на шкале параметров будут поставлены в соответствие границам интервалов шкалы желательности f. Если заранее неизвестны требования конкретных потребителей, данный метод рекомендует придерживаться следующих правил: а) за f = 1,00 принимается уровень параметра, превышающий лучший мировой, или максимально возможный уровень, или уровень, улучшать который не имеет смысла; б) за f = 0,80 принимается лучший мировой уровень, то есть наилучшее значение параметра среди всех рассматриваемых изделий; в) за f = 0,20 принимается самый низкий уровень среди всех рассматриваемых изделий; г) за f = 0,00 принимается наиболее низкий уровень значения исследуемого параметра изделия, который можно себе представить; д) интервал на шкале параметров, соответствующий значениям функции желательности f = 0,20...0,80, следует разбить равномерно. При этом значения параметра p в точках, соответствующих значениям функции желательности 0,37 и 0,63, определяются из уравнения аппроксимации:
В качестве критериев оценки могут быть приняты как количественные, так и качественные измерители. В последнем случае оценки качественного параметра (например, имидж изделия или фирмы, его производящей) могут быть также сделаны в соответствии с рекомендациями, приведенными в табл. 1. Имея оценки уровней отдельных параметров изделия, рассчитываем уровень конкурентоспособности всего изделия с помощью обобщенной функции желательности F:
где f — значение функции желательности для i -го параметра изделия; n — количество анализируемых параметров изделия. Сравнивая значение F различных изделий, определяем изделие, обладающее в данное время наилучшей совокупностью потребительских свойств. Этому изделию будет соответствовать наибольшее значение обобщенной функции желательности. Данный метод страдает также рядом недостатков, а именно: 1) при расчете конкурентоспособности не учитывается различное влияние разных параметров на конкурентоспособность продукции; 2) для каждого из параметров предлагается определять только одну аппроксимирующую функцию. Это не всегда может обеспечить необходимую достоверность расчетов, особенно при использовании в качестве аппроксимирующей линейной функции. В данном случае предлагаем (если возможно получить значения р для всех узловых значений х) строить аппроксимирующую функцию по узловым точкам, ближайшим к значениям параметра изделия; 3) на наш взгляд, экономически необоснованно использование функции Однако использование функции Исследование функции Протабулируем данную функцию на отрезке [–4,0; 10,0] (расширять границы не имеет смысла, так как значения f (–4,0) и f (10,0) близки к предельным) с шагом 0,2. Кроме того, найдем приращение функции желательности на каждом шаге. По полученным значениям построим графики функции желательности и ее приращения (см. рисунок 1). На рисунке 1 хорошо заметна неравномерность изменения функции желательности. Для х Э[–1,8; 5,2] приращение функции составляет больше 0,001; для х Э[–1,4; 3,0] — больше 0,01, а для х Э[–0,6; 0,8] — больше 0,05. Для х Э[–1,8; 5,2] приращение незначительно и стремится к 0. Своего максимума изменения функция желательности достигает вблизи точки х =0. Таким образом, для объектов, у которых Х, т.е. приведенные значения параметра р, относительно близки к 0, различие значений функции желательности будет много больше, чем для объектов, у которых при той же разнице Х приведенные значения параметра отдалены от 0, что искажает действительность.
Рис. 1. Графики функции желательности и ее приращения
|
||||
|
Последнее изменение этой страницы: 2019-10-15; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.48.237 (0.01 с.) |

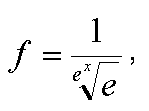 , (9)
, (9)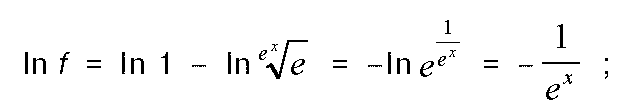
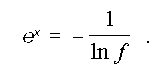 (11)
(11)
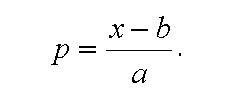 (14)
(14)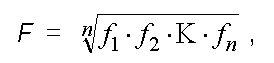 , (15)
, (15)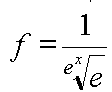 в качестве функции желательности. Очевидно, она была нужна по той причине, что принимает значения от 0 до 1, что для функции желательности предпочтительно.
в качестве функции желательности. Очевидно, она была нужна по той причине, что принимает значения от 0 до 1, что для функции желательности предпочтительно.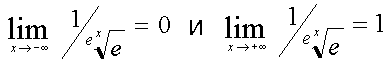 , т.е. ее значения лежат в интервале (0; 1).
, т.е. ее значения лежат в интервале (0; 1).