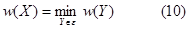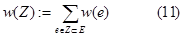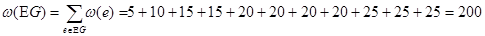Практическое применение жадного алгоритма

 

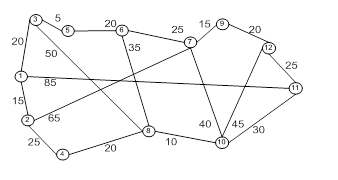
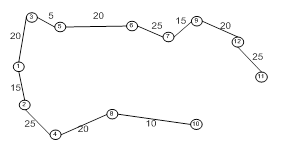
На территории некого города N размещены заводы и магазины, в которые поставляется продукция с этих заводов. В результате разработки были определены возможные трассы для прокладки коммуникаций и оценена стоимость их создания для каждой трассы. Стоимость прокладки коммуникаций для трассы между заводом №1 и магазином удобрений составляет 15 у.е., между заводом №1 и заводом №3 – 85 у.е., между заводом №1 и хлебозаводом – 20 у.е. Между магазином №1 и заводом №2 составит 25 у.е., между магазином №1 и обувной фабрикой – 65 у.е. Стоимость прокладки коммуникаций для трассы, соединяющей хлебозавод и магазин №2 - 5 у.е., между хлебозаводом и кафе – 50 у.е., между заводом №2 и кафе - 20 у.е., между магазином №2 и продуктовым магазином - 20 у.е., между продуктовым магазином и обувной фабрикой - 25 у.е, между продуктовым магазином и кафе – 35 у.е., между обувной фабрикой и магазином №3 - 15 у.е, между обувной фабрикой и аптекой – 40 у.е., между кафе и аптекой - 10 у.е., между магазином №3 и торговым центром - 20 у.е., между аптекой и заводом №3 составит 30 у.е, между аптекой и торговым центром – 45 у.е., между заводом №3 и торговым центром, - 25 у.е. Необходимо, чтобы коммуникации связали все объекты, затраты на прокладку данных коммуникаций должны быть минимальны.

Для удобства записи вводятся следующие обозначения:

V₁ – завод №1, V₂ – магазин №1, V₃ – хлебозавод, V₄ –завод №2, V₅ – магазин №2 V₆ –продуктовый магазин, V₇ – обувная фабрика, V₈ –кафе, V₉ – магазин №3, V₁₀ – аптека, V₁₁ –завод №3, V₁₂ – торговый центр.

Если создать графическую интерпретацию данной модели, то видно что получился граф с 12 вершинами и 18 ребрами.

Рисунок 1– Графическая интерпретация задачи о оптимальной структуре сети

 

Из вышесказанного следует, что данную экономическую задачу можно решить с помощью теории графов. Требуется найти дерево покрытия минимального веса. Задача решается с помощью разновидности «жадного» алгоритма, алгоритма Краскала.

Пусть имеется конечное множество Е, | E |=18, весовая функция w: E ®R⁺ и семейство ℇ⊂ 2^Е. Требуется найти Х Î Е, такое что:

Пусть Е – непустое конечное множество, w: E ®R⁺ - функция, ставящая в соответствие каждому элементу е этого множества неотрицательное действительное число w (e) – вес элемента е. Для Х Í Е вес w (Х) определим как сумму весов всех элементов множества Х:

 

где

 

Другими словами, необходимо выбрать в данном семействе непустое подмножество наименьшего веса.

Сопоставим каждому пункту сети вершину графа G. А каждому ребру этого графа сопоставим число, равное стоимости строительства соответствующей коммуникации: (рисунок 1).

Примером жадного алгоритма служит алгоритм Краскала /3/.

Существует теорема, которая утверждает, что алгоритм Краскала всегда приводит к ребру, имеющему минимальный вес.

Согласно алгоритму Краскала, выбирается ребро минимального веса. В данном случае это будет ребро е₁ = {3,5}, получаем граф Т₁.

Строится граф Т₂ = Т₁ + е₂, где е₂ - ребро, имеющее минимальный вес среди ребер, не входящих в Т₁ и не составляющий циклов с ребрами Т₁, е₂ {8,10}.

 

Т₃ = Т₂ + е₃, где е₃ = {7,9}.

Т₄ = Т₃ + е₄, где е₄ = {1,2}.

Т₅ = Т₄ + е₅, где е₅ = {1,3}.

Т₆ = Т₅ + е₆, где е₆ = {5,6}.

Т₇ = Т₆ + е₇, где е₇ = {4,8}.

Т₈ = Т₇ + е₈, где е₈ = {9,12}

Т₉ = Т₈ + е₉, где е₉ = {2,4}.

Т₁₀ = Т₉ +е₁₀, где е₁₀ = {6,7}.

Т₁₁ = Т₁₀ + е₁₁, где е₁₁ = {11,12}.

 

Найдено минимальное дерево покрытия взвешенного графа, следовательно, найдена и оптимальная структура сети, где общая стоимость затраченная на прокладку коммуникаций составит:

 

и это минимальная сумма затрат из всех возможных. При прокладке коммуникационной сети, соединяющей все данные пункты затрачивается 200 у.е.

Рисунок 2 – Решение задачи о оптимальной структуре сети

 

Коммуникации проложат между следующими пунктами: аптека – кафе - завод №2 – магазин №1 - завод №1 – хлебозавод – магазин №2 - продуктовый магазин – обувная фабрика – магазин №3 – торговый центр.