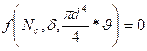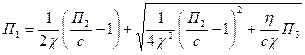Математические модели процесса углубления скважины

Из всех технологических процессов в нефтяной промышленности процесс бурения является самым старым и в то же время наименее теоретически изученным и описанным. В значительной степени это связано со сложностью математического моделирования физических процессов разрушения породы на забое скважины. В связи с этим для получения количественных соотношений для оценивания средней механической скорости проходки v обычно используют эмпирические зависимости вида:

, (2.12)

Или

, (2.13)

где Р -- осевая нагрузка на долото; d -- диаметр долота; n -- число оборотов долота, а,, b и -- параметры модели.

Идентификация параметров в зависимостях (2.12) и (2.13) показывает, что от опыта к опыту их величины меняются, хотя и можно указать пределы их изменения. Так, [0,4-0,8]; величина часто принимается равной единице, хотя есть данные, по которым =0,6; величина параметра а является функцией числа Рейнольдса, рассчитанного для истечения промывочной жидкости из отверстия долота; величина параметра b отождествляется с величиной ()^-1, где --нагрузка на долото, при которой достигается максимальная Скорость проходки. Величина, очевидно, будет зависеть от количества промывочной жидкости, свойств разбуриваемой породы, частоты вращения долота и т. д.

Такая широта трактовки зависимости коэффициентов, моделей от различных параметров процесса вряд ли удобна. Единственный путь несколько ограничить произвольность толковании экспериментальных данных -- строить модели процесса бурения в безразмерной форме, с учетом основных законов сохранения. Попытаемся это сделать, по возможности максимально упростив механизм процессов разрушения породы на забое скважины.

Начнем с очевидного утверждения, что энергия, подводимая извне к инструменту, равна сумме энергетических затрат на разрушение породы в забое, продвижение инструмента и на тепло за счет сил трения при истирании породы. Подводимую к забою энергию мы знаем. При расчете ее на единицу времени можно сказать, что она равна сумме мощностей N₁ и N_2,первая из которых затрачивается на вращение инструмента, а вторая -- на его углубление. В зависимости от разбуриваемой породы, конструкции и состояния инструмента часть мощности N₁ будет расходоваться па преодоление сил трения и истирание породы. Эта часть энергии будет превращаться в тепло, а оставшаяся часть будет расходоваться на механическую работу по разрушению породы. Для выделения последней части введем понятие коэффициента полезного действия инструмента, определив его следующим образом. Если на вращение инструмента к забою подводится мощность N₁,а на разрушение породы тратится только часть этой мощности N₁^*, то:

N₁^*= N₁ (2.14)

Очевидно, величина непостоянна во времени и изменяется как при изменении условий на забое, так и при износе инструмента. В частности, величина должна зависеть от осевой нагрузки на долото.

Если механическая скорость бурения, а осевая нагрузка на долото Р, то вторую составляющую мощности N₂ можно выразить через эти величины и записать в виде:

N₂=Р (2.15)

Таким образом, полная мощность N, затрачиваемая на углубление забоя, определяется равенством:

N= N₁+ Р (2.16)

Часть этой мощности, которую обозначим N _с, расходуется на скалывание породы в забое, а оставшаяся часть N_Дзатрачивается на дробление уже сколотых кусков, если они не сразу были вынесены или попали опять в зону действия инструмента.

Для характеристики прочностных свойств породы забоя введем коэффициент твердости породы. Размерность этой величины []=ML^-1 T^-2. Если не учитывать зависимость N_c от свойств промывочной жидкости, то можно утверждать, что N_c будет функцией а и объема забоя, выбуриваемого в единицу времени и равного величине рd²/4, где d -- диаметр долота. По теории размерности, эти величины должны удовлетворять уравнению:

, (2.17)

которое в безразмерных переменных можно привести к виду

(2.18)

Решением уравнения (2.18) будет

или (2.19)

Здесь с -- неизвестная константа.

Мощность N_Д, которая расходуется на повторное дробление породы, зависит от объема выбуриваемой и единицу времени породы, расхода промывочной жидкости Q, ее плотности и вязкости, среднего размера частей скалываемой породы, плотности породы, коэффициента прочности породы и др. Такое обилие параметров не оставляет надежд на получение простого параметрического выражения для N_л методом теории размерностей.

Поэтому воспользуемся для раскрытия N_Д следующей эмпирической формулой:

, (2.20)

где ч - безразмерный коэффициент, зависящий от свойств промывочной жидкости и особенностей ее подачи, а также от свойств породы.

Приравнивая мощности N и сумму мощностей N_с и N_Д, получим:

(2.21)

Это квадратное уравнение относительно скорости механической проходки. Прежде чем его решать, приведем его к безразмерному виду, вводя новые переменные:

;

; (2.22)

;

где n - число оборотов долота; А - работа, производимая долотом за один оборот, получаем:

(2.23)

Из этого уравнения находим:

(2.24)

Второй корень не удовлетворяет физическим условиям задачи, так как он соответствует отрицательному значению П₁.

Определим интервалы изменения независимых переменных П₂ и П₃. величина Р/d не превышает 12 кН/см для диаметров долот 269-295 мм. Для долот диаметром 214 мм этот предел снижается до 8.5 кН/см. величина для песчаника равна 65 кН/см, а для гранита 220 кН/см. максимальная величина П₂, которую можно получить на основе этих данных, не превосходит 4*10^-4, то есть очень мала. Поскольку величина с в формуле (2.19) не превышает 0,1, можно сделать вывод, что П₂/с«1, и поэтому пренебрегая ей как слагаемым в (2.24) получим:

, =4ч/с (2.25)

Вторя переменная П₃ может изменятся от нуля (n=0,Q?0) до бесконечности (n?0,Q=0).

Проверим асимптотические свойства зависимости (2.25). При снятии осевой нагрузки, то есть при Р=0, а также при остановке инструмента независимо от расхода промывочной жидкости скорость бурения должна стремиться к нулю. То же следует из модели. Если промывочную жидкость не подавать (Q=0), то скорость бурения также будет нулевой, независимо от числа оборотов инструмента и нагрузки на долото. Этот результат также получаем из модели. Сравним теперь количественные зависимости. Как было сказано ранее, по имеющимся данным, скорость бурения пропорциональна n, где [0,4-0,8]. По нашей модели скорость бурения также возрастает при увеличении числа оборотов бура. При условии П₃>>1 можно сказать, что n^0.5, при меньших значениях П₃ влияние изменения числа оборотов бура на скорость бурения уменьшается.

Экспериментальная зависимость скорости бурения от осевой нагрузки на долото также степенная с показателем степени, изменяющимся в пределе 0,6-1. в нашу модель осевая нагрузка в явном виде не вошла, хотя, очевидно, с ней должна быть функционально связана величина А. причем можно предполагать, что эта связь должна быть степенной, так как величина А равна нулю при Р=0 и растет с увеличением Р.

В области малых расходов промывочной жидкости, когда число Рейнольдса, рассчитанное для течения жидкости в отверстии долота, лежит в пределах 2-100, скорость бурения пропорциональна числу Рейнольдса (или расходу жидкости при фиксированных остальных параметрах). Из нашей модели мы получаем тот же результат в области П₃<<1. В области П₃>>1 скорость бурения будет пропорциональна корню квадратному из расхода промывочной жидкости.

Подводя итог проведенному анализу, можно сделать вывод, что зависимость (2.25) удовлетворяет основным экспериментальным результатам. В отличие от известных трехпараметрических зависимостей (2.12) и (2.13) в нее входят только два параметра, подлежащие определению, а связывает она не четыре, а пять исходных размерных переменных.