
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напряжение в грунте от собственного веса грунта.Содержание книги
Поиск на нашем сайте
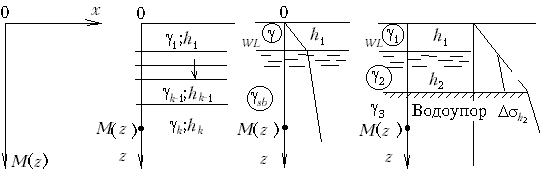
Вертикальное напряжение от собственного веса грунта s z представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке M на глубине z грунт однородный, получаем s z = g z, если имеются различные слои (рис.М.6.1), то
Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде, поэтому получаем
Давление s z в водоупорном слое принимается с учетом полного веса водонасыщенного грунта (то есть выталкивающая сила не учитывается), который расположен выше:
На границе водоупора в эпюре s z имеет место скачок на величину Деформации грунта от его собственного веса обычно не учитываются, так как они давно завершились. Однако в том случае, если в силу обстоятельств изменяется структура грунта, то сила собственного веса грунта вызывает в нем дополнительные деформации (например, при увлажнении лессового грунта, изза которого растворяются жесткие цементационные связи, или оттаивания вечномерзлого грунта). Боковые напряжения s х составляют обычно долю от вертикальных, то есть s х =x 0s z. Коэффициент бокового давления грунта в условиях его естественного залегания x 0 равен отношению бокового давления s x к вертикальному s z. (а не отношению приращений этих давлений), то есть не следует путать x 0 и x. Коэффициент x 0 может быть как больше, так и меньше единицы. 31.Напряжение в грунте от сосредоточенной силы (основная задача). Основным является решение задачи о сосредоточенной силе, приложенной к поверхности полупространства перпендикулярно к граничной плоскости (задача Буссинеска). Для решения задач о нагрузке, имеющей горизонтальную составляющую, рассматривается дальнейшее развитие решения этой же задачи, но при сосредоточенной силе, действующей вдоль граничной плоскости (как бы "прикрепленной" к ней в одной точке, рис. М.7.1.). Аналогичные решения задач о сосредоточенных силах вертикальной и горизонтальной, то есть приложенных перпендикулярно (решение Фламана) и по касательной к границе полуплоскости, также являются основными. Из них путем интегрирования могут быть получены многие решения интересующих нас в практических целях задач.
Задача эта является абстрактной, так как в действительности усилия всегда распределяются по некоторой площадке. Непосредственно под сосредоточенной силой напряжения являются бесконечно большими. Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы. В месте приложения сосредоточенной силы, непосредственно совпадающем с началом координат (так проще решить задачу), действует эта сила, а во всех остальных точках границы никаких сил не действует. В точках, бесконечно удаленных от места приложения силы, напряжения должны стремиться к нулю. Напряжениеs R является основным. Это напряжение пропорционально косинусу угла между радиусомвектором и вертикалью, обратно пропорционально квадрату радиуса и прямо пропорционально величине действующей силы. В решении этой задачи, вследствие имеющейся симметрии, участвуют две координаты - радиус и угол между ним и вертикалью.
|
|||||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 390; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.009 с.) |


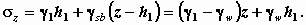

 , причем в данном случае
, причем в данном случае  .
.




