
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейные взаимосвязи и неравная изменчивостьСодержание книги
Поиск на нашем сайте
Методы множественной регрессии, которые мы до сих пор обсуждали, основываются на линейной модели множественной регрессии, которая характеризуется постоянной изменчивостью. Если вашейсовокупности данных не присуща подобная линейная взаимосвязь, на что может указывать диагностическая диаграмма, которую мы исследовали выше, у вас есть три варианта действий. Первые два предусматривают применение множественной регрессии и описаны в настоящем разделе. 1. Преобразовать некоторые (или все) переменные. Преобразуя одну или несколько переменных (например, с помощью логарифмов), иногда удается получить новую совокупность данных, характеризующуюся линейной взаимосвязью. Помните, что логарифмы можно использовать для преобразования лишь положительных чисел. Если ваша совокупность данных характеризуется неравной изменчивостью, с этой проблемой можно справиться путем преобразования Y и (возможно) некоторых из Х-переменных. 2. Ввести новую переменную. Ввод дополнительной, необходимой переменной X (например, Х12) иногда позволяет получить линейную взаимосвязь между Y и новой совокупностью Х-переменных. Такой метод может быть удачным, когда вам требуется найти оптимальное значение Y, например максимизировать прибыль или выпуск продукции. В других ситуациях можно использовать произведения переменных (например, определив Х5 = Х1 * Х2), чтобы уравнение регрессии отражало взаимодействие между этими двумя переменными. 3. Использовать нелинейную регрессию. Иногда в данных может присутствовать важная нелинейная взаимосвязь (возможно, имеющая под собой определенное теоретическое обоснование), которую необходимо оценить непосредственно. В таких случаях можно воспользоваться более сложными методами нелинейной регрессии — если нам известны вид этой взаимосвязи и вид случайности.
Преобразование взаимосвязи в линейную форму: интерпретация результатов
Выполняя преобразование своих данных, следует иметь в виду одну полезную рекомендацию. Чтобы избежать чрезмерного усложнения задачи, пытайтесь использовать одно и то же преобразование для всех переменных, которые измеряются в одних и тех же единицах. Если, например, вы логарифмируете объем продаж (который измерен в долларах или тысячах долларов), вам, вероятно, следует преобразовать таким же способом и все другие переменные, измеренные в долларах. При этом долларовые величины для всех соответствующих переменных будут измеряться по процентной шкале, а не по абсолютной “долларовой” шкале (именно в этом и заключается результат логарифмирования). Ко всем переменным, измеренным в одинаковых базовых единицах, желательно применять одно и то же преобразование. Если вы выполняете множественный регрессионный анализ после преобразования всех или некоторых из переменных, то некоторые результаты могут требовать новой интерпретации. Ниже будет показано, как интерпретировать результаты множественного регрессионного анализа, когда либо (1) Y не подвергается преобразованиям (т.е. преобразуются лишь некоторые или все Х-переменные), либо (2) Y преобразуется с помощью натурального логарифма (независимо от того, преобразуются все или некоторые из Х-переменных). Переменная Y играет особую роль, поскольку именно ее мы пытаемся прогнозировать. Поэтому преобразование Y переопределяет смысл ошибки прогнозирования. Табл. 12.3.1 содержит интерпретацию основных результатов компьютерных вычислений: коэффициента детерминации, R2; стандартной ошибки оценки, Se; коэффициентов регрессии, bi; и проверки значимости для bi в случае использования преобразований. Включена также процедура нахождения с помощью уравнения регрессии прогнозируемых значений Y.
Значение R2 имеет одну и ту же базовую интерпретацию, независимо от того, как именно вы преобразуете свои переменные. Это значение говорит о том, какая доля изменчивости вашего текущего Y (в любой — преобразованной или не преобразованной — форме) объясняется текущей формой Х-переменных. Стандартная ошибка оценки, Se, имеет разную интерпретацию в зависимости от того, выполнялось ли преобразование Y. Если переменная Y не преобразовывалась, применяется обычная интерпретация (типичная величина ошибок прогнозирования), поскольку прогнозируется сама переменная Y. Однако если в регрессионном анализе используется log Y, то Y фигурирует в регрессии в процентах, а не в абсолютных значениях соответствующих единиц измерения. Подходящей мерой относительной изменчивости, в соответствии с материалом главы 5 является коэффициент вариации, поскольку та же изменчивость процентов будет как для высоких, так и для малых прогнозируемых значений Y. Формула для этого коэффициента вариации в табл. 12.3.1 базируется на теории т.н. логнормального распределения. Коэффициенты регрессии, bi, если переменная Y не подвергалась преобразованиям, имеют обычную интерпретацию: они показывают ожидаемое влияние увеличения Xi на Y, причем единица увеличения Хi зависит от того, какому преобразованию подвергалась Xi. Если же переменная Y подвергалась преобразованиям, то bi указывает на изменение в преобразованной переменной Y. Если вы использовали и логарифм переменной Y, и логарифм Хi, то bi имеет специальную экономическую интерпретацию эластичности. Эластичность Y по отношению к Xi представляет собой ожидаемое процентное изменение Y, связанное с увеличением Хi на 1% при неизменных значениях других Х-переменных; эластичность оценивается с помощью коэффициента регрессии из уравнения, где используются натуральные логарифмы как Y, так и Xi. Таким образом, эластичность — это почти то же самое, что и коэффициент регрессии, за исключением того, что изменения выражаются в процентах, а не в исходных единицах измерения. Проверка значимости для коэффициента регрессии bi сохраняет свою обычную интерпретацию для любых приемлемых вариантов преобразования. Главный вопрос заключается в следующем: оказывает ли Xi ощутимое влияние на Y (при условии, что другие Х-переменные остаются неизменными) или Y ведет себя случайно по отношению к Х? Поскольку ответом на этот вопрос является не подробное описание, а лишь “да” или “нет”, основной предмет проверки остается тем же, независимо от того, выполняем мы логарифмическое преобразование или нет. Разумеется, в каждом отдельном случае проверка значимости выполняется по-своему, а полученные результаты оказываются наилучшими в том случае, когда используемые вами преобразования приводят к линейной модели множественной регрессии для ваших данных. Прогнозирование Y весьма существенно зависит от того, подвергалась ли Y преобразованиям. Если переменная Y не подвергалась преобразованиям, уравнение регрессии прогнозирует Y непосредственно. Достаточно для каждой Xi взять соответствующим образом преобразованные значение, умножить его, на коэффициент регрессии bi, сложить все эти произведения, добавить а — и вы получаете прогнозируемое значение Y. Преобразование переменной Y с помощью натурального логарифма может привести к коррекции имеющейся до преобразования у переменной Y асимметрии. Использование в уравнении регрессии надлежащим образом преобразованных значений Х-переменных дает прогноз log Y. Новая процедура прогнозирования исходной (непреобразованной) переменной Y, представленная в приведенной выше таблице, делает две вещи. Во-первых, путем экспоненцирования прогнозированное значение log Y преобразуется к исходным единицам Y. Во-вторых, коррекция асимметрии (основанная на Se) увеличивает это значение, отражая тот факт, что среднее значение больше, чем медиана или мода для этого вида асимметричного распределения.
Пример. Рекламные объявления в журналах: использование преобразования и интерпретация
В табл. 12.3.2 представлены результаты множественной регрессии для нашего примера с рекламными объявлениями в журналах после преобразования с помощью логарифма тарифа на размещение рекламы в журналах, величины читательской аудитории и медианы дохода. Теперь мы имеем дело с логарифмом тарифа на размещение рекламы в журналах (новая переменная У), который объясняется логарифмом величины читательской аудитории (новая переменная X,), процентом читателей-мужчин (переменная Х2) и логарифмом медианы дохода (новая переменная Х3). Попытаемся интерпретировать полученные результаты.
Значение R2=80,5% интерпретируется обычным образом, как и в терминах исходных (непреобразованных) переменных. Это значение свидетельствует о том, что 80,5% изменчивости величины тарифа на размещение рекламы в различных журналах могут объясняться известными для каждого журнала значениями размера читательской аудитории, процента читателей-мужчин и медианы дохода читателей. Смысл R2 не меняется, независимо от того, проводились ли логарифмические преобразования, но детали несколько разнятся. Стандартная ошибка оценки, Se = 0,2603, получает новую интерпретацию. Чтобы придать смысл этому числу (которое буквально означает типичную величину ошибок прогнозирования на логарифмической шкале), воспользуемся следующим уравнением:
Это свидетельствует о том, что ваша ошибка прогнозирования в типичном случае составляет 26,5% от прогнозируемого значения. Если, например, ваш прогнозируемый тариф на размещение рекламы в журнале равен $ 100 000, вариация составляет 26,5% от этого значения, или $26 500, что дает стандартную ошибку оценки для тарифа на размещение рекламы в журналах, которое вполне применимо к такого рода очень большим журналам. Если же ваш прогнозируемый тариф на размещение рекламы в журналах равен $20 000, взяв 26,5% от этого значения, получим $5 300 как соответствующую стандартную ошибку для подобного рода небольших журналов. В том, что стандартная ошибка оценки должна зависеть от масштаба журнала, есть определенный смысл, поскольку большие журналы имеют гораздо больше возможностей для изменчивости, чем небольшие. Коэффициент регрессии b1 = 0,578 (для логарифма величины читательской аудитории) представляет собой эластичность, поскольку преобразование с помощью натуральных логарифмов использовалось и для Y. Таким образом, увеличение читательской аудитории на 1 % позволяет нам рассчитывать на увеличение тарифа на размещение рекламы в журнале на 0,578%. Это указывает на наличие эффекта уменьшенного отклика, в результате которого увеличение читательской аудитории на 1% приводит к несколько меньшему (т.е. меньше, чем на 1%) увеличению тарифа на размещение рекламы. У вас может возникнуть вопрос, действительно ли это уменьшение является значимым или коэффициент b1 = 0,578, по существу, равен 1 — если не принимать во внимание действие случайного фактора. Ответ заключается в том, что указанное заданное значение 1 находится за пределами доверительного интервала для b1 (который расположен между 0,498 и 0,659), а это свидетельствует о значимом уменьшении. К этому выводу можно было бы прийти и другим путем — вычислив t-статистику: t = (0,578 – 1)/0,0402 = - 10,5. Оказывает ли величина читательской аудитории значимое влияние на величину рекламного тарифа, если процент читателей-мужчин и средний доход остаются неизменными? Ответ на этот вопрос является положительным, о чем свидетельствует обычный t-тест значимости b1 в данной множественной регрессии. К этому выводу можно прийти на основе p-значения (в табл. 12.3.2 это значение равняется 0,000 для независимой переменной "log Аудитория"). И наконец, давайте определим прогнозируемое значение Y для журнала Audubon. Это значение будет несколько отличаться от прогнозируемого значения, вычисленного намного раньше в этой главе; к тому же оно оказывается несколько лучшим, так как до преобразования исследуемые данные не соответствовали модели линейной множественной регрессии. Прогнозирование Y выполняется в два этапа: сначала мы прогнозируем log Y непосредственно из уравнения регрессии, а затем используем Se для получения прогнозируемого значения. Журнал Audubon характеризуется следующими значениями: X1 = 1 645 (т.е. читательская аудитория этого журнала равна 1,645 миллиона человек), Х2 = 51,1 (указывает на то, что среди читателей этого журнала 51,1% мужчин) и Х3 = $38 787 (указывает медиану дохода семьи читателей этого журнала). Преобразуя в уравнении регрессии величины читательской аудитории и среднего дохода с помощью логарифма, находим прогнозируемое значение для log (тариф на размещение рекламы в журналах) для журнала Audubon. Прогнозируемое значение log (тариф на размещение рекламы в журналах) = -3,441 + 0,57847 * log(Аудитория) - 0,001635*(процент читателей-мужчин) + + 0,8897 *log(Доход) = = -3,441 +0,57847 *log(1 645)-0,001635(51,1) + 0,8897 * 1оg(38 787) = = -3,441 + 0,57847 * 7,4055 - 0,001635(51,1) + 0,8897 * 10,5658 = = -3,441 + 4,2839 - 0,0835 + 9,4004= 10,160. Чтобы найти прогнозируемое значение тарифа на размещение рекламы в журналах, нужно выполнить следующий этап: прогнозируемый тариф на размещение рекламы в журналах =
Это прогнозируемое значение сравнимо с фактической величиной рекламного тарифа для этого журнала — $25 315. Нам повезло, что эти значения достаточно близки друг к другу. Соответствующая стандартная ошибка для сравнения фактического и прогнозируемого значений составляет 26,5% от $26 739, что равняется $7 086. Если вы вычислите прогнозируемую величину рекламного тарифа для других журналов, то окажется, что они, как правило, не настолько близки к фактическим значениям, как в рассмотренном нами случае. Для сравнения можно взглянуть на относительные ошибки прогнозирования для первых десяти журналов из всего перечня журналов в нашем примере: -5,6%; 11,3%; 27,7%; -23,3%; 9%; 0,9%; 18,8%; 8,0%; -88,0% и -21,6%. Исходя из этого, величина 26,5% представляется вполне приемлемым вариантом типичной величины ошибок.
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 529; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.98.39 (0.007 с.) |

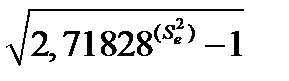 =
= 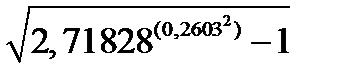 =
=  = 0.265 или 26,5%
= 0.265 или 26,5% = 2,71828[(1/2)*0,2603*0,2603+10,160] = 2,7182810,1939 = $26 739.
= 2,71828[(1/2)*0,2603*0,2603+10,160] = 2,7182810,1939 = $26 739.


