
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 11. Принцип относительности в механикеСодержание книги
Поиск на нашем сайте
Вопрос 1.Принцип относительности Галилея. В классической механике был известен принцип относительности Галилея, согласно которому во всех ИСО все законы механики имеют один и тот же вид, или, иначе говоря, законы механики инвариантны относительно преобразований координат Галилея.
Вопрос 2. Постулаты специальной теории относительности(СТО). 1. Во всех ИСО все законы природы имеют одинаковую математическую форму при использовании преобразований координат и времени Лоренца или, иначе, все законы природы инвариантны относительно преобразований Лоренца. 2. Скорость света в вакууме одинакова во всех направлениях в ИСО и не зависит от движения источника и приемника света.
Использование преобразований Лоренца приводит к «необычным» с точки зрения классической механики выводам, что в разных ИСО: 1) длина данного тела различна, 2) длительность одного и того же события – различна, 3) два одновременно происходящих события оказываются неодновременными в разных ИСО. Вопрос 3. Сокращение длины. l0 – длина стержня в системе, относительно которой он покоится (в нашем случае в К), l – длина этого отрезка в системе, относительно которой он движется (К¢). Таким образом, из СТО следует, что размеры движущихся тел должны сокращаться в направлении их движения, но реального сокращения нет, т.к. все ИСО равноправны. Вопрос 4. Замедление времени.
Таким образом, движущиеся часы должны идти медленнее. Dt0 – время по часам, движущимся вместе с телом («событием») называется собственным временем. Вопрос 5. Интервал между событиями. Согласно классической механике пространство и время никак не связаны между собой. Пространственный интервал определяется разностями соответствующих координат:
Согласно СТО пространство и время неразрывно связаны друг с другом. Иначе говоря, мир, в котором мы живем, является четырехмерным (3 координаты и время), поэтому вместо слова «отрезок» следует говорить «пространственно-временн о й интервал, включающий в себя кроме координат еще и время.
Пространственно-временной интервал sСТО является инвариантом при использовании преобразований Лоренца, т.е. имеет один и тот же вид в любой ИСО. Это можно показать, используя преобразования Лоренца (рекомендуем студентам проделать это самостоятельно для случая Dy= 0, Dz = 0). Вопрос 6. Релятивистский закон сложения скоростей. Найдем скорость 1-го фотона в системе отсчета К¢, связанной со 2-ым фотоном, используя классическую формулу для сложения скоростей:
Таким образом, скорость одного фотона в системе отсчета, связанной со 2-ым, оказалась равной 2 с, но согласно СТО ни одна частица не может двигаться со скоростью, большей скорости света.
Вычислим теперь скорость фотона из предыдущего примера по релятивистской формуле.
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 314; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.14.251 (0.007 с.) |


 - радиус-вектор точки М в неподвижной системе отсчета К,
- радиус-вектор точки М в неподвижной системе отсчета К,  - в движущейся системе К¢,
- в движущейся системе К¢, 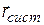 - радиус-вектор, проведенный из точки О в точку О¢
- радиус-вектор, проведенный из точки О в точку О¢

 - скорость точки М в К,
- скорость точки М в К,  - скорость точки в К¢,
- скорость точки в К¢,  - скорость системы К¢ относительно системы К.
- скорость системы К¢ относительно системы К.



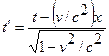

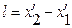
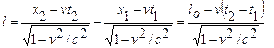

 , т.к.
, т.к.  и
и  .
. выразим длительность события в К¢, используя преобразования Лоренца, получим:
выразим длительность события в К¢, используя преобразования Лоренца, получим: 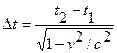 ,
, 
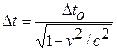 , Dt > Dt0, выражение, связывающее между собой длительность данного события в разных ИСО; Dt0 - длительность события в К, Dt – длительность этого события в К¢.
, Dt > Dt0, выражение, связывающее между собой длительность данного события в разных ИСО; Dt0 - длительность события в К, Dt – длительность этого события в К¢. (пространственный интервал (отрезок) в классической механике).
(пространственный интервал (отрезок) в классической механике). (пространственно-временной интервал в СТО).
(пространственно-временной интервал в СТО).










