Дифференциальные уравнения плоского движения твердого тела.

Физический маятник.

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Дифференциальное уравнение движения физического маятника

Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

.

Полагая , предыдущее уравнение можно переписать в виде:

.

Последнее уравнение аналогично уравнению колебаний математического маятника длиной. Величина называется приведённой длиной физического маятника.

Центр качания физического маятника

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии l от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . Легко заметить, что уравнение движения не изменится.

Элементарная и полная работа силы. Мощность.

Работа силы.

Мерой действия силы при превращении механического движения в другую форму движения является работа силы.

Работа постоянной по модулю и направлению силы F на прямолинейном перемещении s ее точки приложения равна

Если угол α острый, то работа силы положительна, если тупой – отрицательна.

Если направления силы и перемещения совпадают (α=0), то A = Fs;

Если направление силы перпендикулярно направлению перемещения (α=90◦), то А = 0;

Если направление силы противоположно направлению перемещения (α=180◦), то A = -Fs.

Элементарная работа силы F на перемещении точки из одного положения в другое по криволинейной траектории

δA = Fδs cos (F,v),

где δs – пройденный точкой элементарный путь;

∠F, v – угол, составленный направлением силы F и скоростью v.

В случае переменной силы определяется элементарная работа на малом перемещении, и после суммирования элементарных работ получается

Мощность

Мо́щность — физическая величина, равная в общем случае скорости изменения энергии системы. В более узком смысле мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.

Различают среднюю мощность за промежуток времени

и мгновенную мощность в данный момент времени:

Интеграл от мгновенной мощности за промежуток времени равен полной переданной энергии за это время:

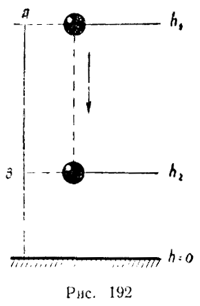
Работа силы тяжести и силы упругости.

Работа силы тяжести

Сила тяжести равна F = mg и направлена по вертикали вниз. Вблизи поверхности Земли ее можно считать постоянной.

При движении тела по вертикали вниз сила тяжести совпадает по направлению с перемещением. При переходе с высоты h1 над каким-то уровнем, от которого мы начинаем отсчет высоты, до высоты h2 над тем же уровнем (рис. 192), тело совершает перемещение, по абсолютной величине равное h1 - h2.

 

Так как направления перемещения и силы совпадают, то работа силы тяжести положительна и равна:

Высоты h1 и h2 не обязательно отсчитывать от поверхности Земли. Для начала отсчета высот можно выбрать любой уровень. Это может быть пол комнаты, стол или стул, это может быть и дно ямы, вырытой в земле, и т. д. Ведь в формулу для работы входит разность высот, а она не зависит от того, откуда начинать их отсчет. Мы могли бы, например, условиться начинать отсчет высоты с уровня В (см. рис. 192). Тогда высота этого уровня была бы равна нулю, а работа выражалась бы равенством

A=m*g*h

где h — высота точки A над уровнем В.

 

Работа силы упругости

Сила упругости, как мы знаем, возникает при деформации тел. По своему абсолютному значению она пропорциональна величине деформации (удлинению), а направлена в сторону, противоположную направлению смещения точек тела при деформации.

На рисунке 199, а показана пружина в ее естественном, недеформированном состоянии. Правый конец пружины закреплен, а к левому прикреплено тело. Если пружину сжать, сместив левый ее конец па расстояние x1 (рис. 199, б), то возникнет сила упругости, действующая со стороны пружины на тело, равная:

F1упр=—kx1

где k — жесткость пружины.

Предположим, что левый конец пружины переместился из положения А в положение В (рис. 199, в). В этом положении деформация пружины равна уже не х1, а х2. Значит, конец пружины переместился на расстояние х2 — х1. Чтобы вычислить работу, нужно это перемещение умножить на силу. Но сила упругости в отличие от силы тяжести вблизи поверхности Земли при движении тела изменяется от точки к точке. Если в начальной точке она была равна —kx1, то в конечной точке (в точке В) она стала равной —kx2.

Для того чтобы вычислить работу силы упругости, нужно взять среднее значение силы упругости и умножить его на перемещение х2 — х1.

Сила упругости пропорциональна деформации пружины. Поэтому среднее значение силы упругости можно найти, используя метод, который был использован при нахождении среднего значения скорости при равноускоренном движении.

На это-то значение силы упругости и нужно умножить перемещение х2 — х1 чтобы получить работу этой силы:

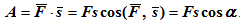
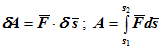
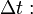
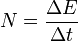
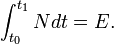
Так как 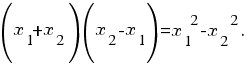то формула для работы принимает вид: