Указания к решению задачи 1.

Задача 1 относится к расчету выпрямителей переменного тока, собранных на полупроводниковых диодах. Подобные схемы широко применяются в различных электронных устройствах и приборах. При решении задач следует помнить, что основными параметрами полупроводниковых диодов являются допустимый ток Iдоп, на который рассчитан данный диод, и обратное напряжение Uобр, выдерживаемое диодом без пробоя в непроводящий период.

Обычно при составлении реальной схемы выпрямителя задаются значением мощности потребителя Ро, Вт, получающего питание от данного выпрямителя, и выпрямленным напряжением Uо, В, при котором работает потребитель постоянного тока. Отсюда нетрудно определить ток потребителя Iо = Pо/Uо. Сравнивая ток потребителя с допустимым током диода Iдоп, выбирают диоды для схем выпрямителя. Следует учесть, что для однополупериодного выпрямителя ток через диод равен току потребителя, т.е. надо соблюдать условие Iдоп ≥ Iо. Для двухполупериодной и мостовой схем выпрямления тока через диод равен половине тока потребителя, т.е. следует соблюдать условие Iдоп ≥ 0.5Iо. Для трехфазного выпрямителя ток через диод составляет треть

тока потребителя, следовательно, необходимо, чтобы Iдоп ≥ I₀

Напряжением, действующее на диод в непроводящий период Ub, также зависит от той схемы выпрямления, которая применяется в конкретном случае. Так, для однополупериодного и двухполупериодного выпрямителя Ub = πUо = = 3.14 Uо, для мостового выпрямителя Ub = 2π Uо /2 = 1.57 Uо, а для трехфазного выпрямителя Ub = 2.1 Uо. При выборе диода, следовательно, должно соблюдаться условие Uобр ≥ Ub.

Рассмотрим примеры на составление схем выпрямителей.

Пример 1.1. Составить схему мостового выпрямителя, использовав один из четырех диодов: Д218, Д222, КД202Н, Д215Б. Мощность потребителя Ро = 300В, напряжение потребителя Uо = 200В.

Р е ш е н и е. 1. Выписываем из табл.1.9 параметры указанных диодов и записываем их в таблицу.

Типы диодов	Iдоп,. А	Uобр, В	Типы диодов	Iдоп, А	Uобр, В
Д218	0.1		КД202Н
Д222	0.4		Д215Б

2. Определяем ток потребителя Iо = Pо/ Uо = 300/200 = 1.5 A.

3. Находим напряжение, действующее на диод в непроводящий период для мостовой схемы выпрямителя, Ub = 1.57 Uo = 1.57 * 200 = 314В.

4. Выбираем диод из условия Iдоп > 0.5Iо > 0.5 * 1.5 > 0.75 А, Uобр > UВ ≥ 314 В. Эти условиям удовлетворяет диод КД202Н: Iдоп = 1.0 > 0.75А; Uобр = 500 > 314В.

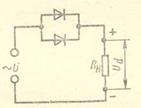
Диоды Д218 и Д222 удовлетворяют напряжению (1000 и 600 больше 314В), но не подходят по допустимому току (0.1 и 0.4 меньше 0.75А). Диод 215Б, наоборот, подходит по допустимому току (2 > 0.75А), но не подходит по обратному напряжению (200 < 314В).

5. Составляем схему мостового выпрямителя (рис. 1). В этой схеме каждый из диодов имеет параметры диода КД202Н; Iдоп = 1А; Uобр = 500В.

рис.1 рис.2

Пример 1.2. Для питания постоянным током потребителя мощностью Ро = =250Вт при напряжении Uо = 100В необходимо собрать схему двухполупериодного выпрямителя, использовав стандартные диоды типа Д243Б.

Р е ш е н и е. 1. Выписываем из таблицы 1.9 параметры диода Iдоп = 2А; Uобр = 200В.

2. Определяем ток потребителя: Iо = Pо/ Uо = 250/100 = 2.5 A.

3. Определяем напряжение, действующее на диод в непроводящий период:

UВ = 3.14 Uо = 3.14 * 100 = 314 B.

4. Проверяем диод по параметрам Iдоп и Uобр. Для данной схемы диод должен удовлетворять условиям Uобр ≥ UВ и Iдоп > 0.5 Iо. В данном случае первое условие не соблюдается (200< 314), т.е. Uобр < UВ; второе выполняется

(0.51 Iо = 0.5 * 2.5 = 1.25 < 2 A).

5. Составляем схему выпрямителя. Чтобы выполнялось условие Uобр > UВ, необходимо два диода соединить последовательно, тогда Uобр = 200 * 2 = = 400 > 314В. Полная схема рис. 2.

Пример 1.3. Для питания постоянным током потребителя мощностью Ро = 20В необходимо собрать схему однополупериодного выпрямителя, использовав имеющиеся стандартные диоды Д242А.

Р е ш е н и е. 1. Выписываем из таблицы 1.9 параметры диода: Iдоп = 10А, Uобр = 100В.

2. Определяем ток потребителя Iо = Pо/ Uо = 300/200 = 15 A.

3. Определяем напряжение, действующее на диод в непроводящий период: Ub = 3.14 Uo = 3.14 * 20 = 63В.

4. Проверяем диод по параметра Iдоп и Uобр. Для данной схемы диод должен удовлетворять условиям Uобр > Ub, Iдоп > Iо. В данном случае второе условие не соблюдается (10 < 15А, т.е Iдоп < Iо). Первое условие выполняется (100 > 63В).

5. Составляем схему выпрямителя. Чтобы выполнялось условие Iдоп > Iо, надо два диода соединить параллельно, тогда Iдоп = 2 * 10 = 20А; 20 > 15А. Полная схема выпрямителя приведена на рис. 3.

Пример 1.4. Для составления схемы трехфазного выпрямителя на трех диодах заданы диоды Д243. Выпрямитель должен питать потребитель с Uо = = 150В. Определить допустимую мощность потребителя и пояснить составления схемы выпрямителя.

Р е ш е н и е. 1. Выписываем из таблицы 2.8 параметры диода: Iдоп = 5А, Uобр = 200В.

2. Определяем допустимую мощность потребителя. Для трехфазного выпрямителя Iдоп > 1 Iо, т.е. Ро = 3Uо Iдоп 3 * 150 * 5 = 2250 Вт.

Следовательно, для данного выпрямителя Ро ≥ 2250 Вт.

3. Определяем напряжение, действующее на диод в непроводящий период:

Ub = 2.1 Uo = 2.1 * 150 = 315В.

 

4. Составляем схему выпрямителя. Проверяем диод по условию. В данном случае это условие не выполняется (200 < 315В). Чтобы это условие выполнялось, необходимо в каждом плече выпрямителя два диода соединить последовательно, тогда Uобр = 200 * 2 = 400В; 400 > 315В. Полная схема выпрямителя приведена рис. 4.

 

Рис.3 Рис.4

 

 

Указания к решению задачи 2.

В этой задаче необходимо выполнить арифметические операции с двоичными числами, которые используются при работе ЭЦВМ. Характерной особенностью двоичной системы счисления является то, что арифметические действия в ней очень просты.

При сложении двоичных чисел пользуются следующим правилом:

0 + 0 = 0; 1 + 0 = 1

0 + 1 = 1; 1 + 1 = 10 (два).

При сложении необходимо учитывать, что 1 + 1 дают нуль в данном разряде и единицу переноса в следующий разряд.

Пример 2.1. Сложить в двоичной системе числа 38 и 28.

1. Переводим данные числа в двоичную систему. Для перевода чисел из одной системы счисления в другую пользуются следующим правилом. Чтобы перевести число из одной системы счисления в другую, необходимо последовательно делить это число на основание новой системы до тех пор, пока не получится частное, меньшее делителя. Число в новой системе следует записывать в виде остатков деления, начиная с последнего, т.е. справа налево. Последнее частное дает старшую цифру числа в новой системе счисления. Напомним, что основание двоичной системы –2, десятичной –10.

 

 

2. Выполняем операцию сложения

100110 38

+ 11100 + 28

---------- ------

1000010 66

 

3. Проверяем решение

1000010 = 1 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 0 * 2³ + 0 * 2² + 0 * 2¹ + 0 * 2⁰ = 66.

Приводим правила вычитания двоичных чисел:

0 – 0 = 0; 1 – 1 = 0

1 - 0 = 1; 10 – 1 = 1.

При вычитании многоразрядных двоичных чисел может возникнуть необходимость заема единицы в ближайшем старшем разряде, что дает две единицы младшего разряда. Если в соседних старших разрядах стоят нули, то приходится занимать единицу через несколько разрядов. При этом единица, занятая в ближайшем значащем старшем разряде, дает две единицы в младшем разряде и единицы во всех нулевых разрядах, стоящих между младшим и тем старшим разрядом, у которого брали заем.

Например:

10010 (18)

- 101 (5)

----------------

1101 (13)

Проверяем решение:

1101 = 1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 1 * 8 + 1 * 4 + 0 * 2 + 1 * 1 = 13.

 

 

Приводим правила умножения двоичных чисел:

0 * 0 = 0; 1 * 0 = 0

0 * 1 = 0; 1 * 1 = 1.

Умножение двоичных чисел производят по тем же правилам, что и для десятичных чисел. При этом используют таблицу умножения и сложения. Умножение многоразрядных двоичных чисел сводится к умножению множимого на каждый разряд множителя, последующему сдвигу множимого или множителя и суммированию получающихся частичных произведений.

Например,

11011 (27)

* 101 (5)

-------------------

+ 11011

-------------------

1000011 (135)

Проверяем решение:

10000111 = 1 * 2⁷ + 0 * 2⁶ + 0 * 2⁵ + 0 * 2⁴ + 0 * 2³ + 1 * 2² * 1 * 2¹ + 1 * 2⁰ =

= 1 * 128 + 0 * 64 + 0 * 32 + 0 * 16 + 0 * 8 + 1 * 4 + 1* 2 + 1 * 1 = 135

При делении двоичных чисел используются таблицу умножения и вычитания. Правила деления аналогичны делению в десятичной системе и сводятся к выполнению умножений, вычитаний и сдвигов.

Например, разделить 117 на 9;

1110101 1001

- 1001 1101

- 1001

-1001

117 9

- 9 13

-----

27

Проверяем решение:

1101 = 1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰ = 1 * 8 + 1 * 4 + 0 * 2 + 1 * 1 = 13