
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения линии конечной длиныСодержание книги
Поиск на нашем сайте
Постоянные
определяются на основании граничных условий.
Тогда из (5) и (6) получаем
откуда
Подставив найденные выражения
Уравнения (7) и (8) позволяют определить ток и напряжение в любой точке линии по их известным значениям в начале линии. Обычно в практических задачах бывают заданы напряжение
Обозначив
откуда
После подстановки найденных выражений
Уравнения длинной линии как четырехполюсника В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.
Определение параметров длинной линии из опытов Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ). При ХХ
При КЗ
На основании (13) и (14)
и
откуда
Выражения (15) и (16) на основании данных эксперимента позволяют определить вторичные параметры
Линия без потерь Линией без потерь называется линия, у которой первичные параметры
откуда Раскроем гиперболические функции от комплексного аргумента
Тогда для линии без потерь, т.е. при
Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.211.49 (0.009 с.) |

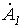 и
и  в полученных в предыдущей лекции формулах
в полученных в предыдущей лекции формулах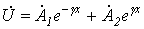 ;
;

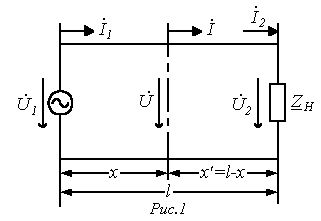 Пусть для линии длиной l (см. рис. 1) заданы напряжение
Пусть для линии длиной l (см. рис. 1) заданы напряжение  и ток
и ток  в начале линии, т.е. при
в начале линии, т.е. при  .
.


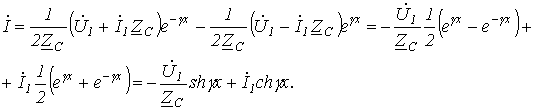
 и ток
и ток 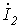 в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде
в конце линии. Для выражения напряжения и тока в линии через эти величины перепишем уравнения (5) и (6) в виде ;
;
 .
.
 и
и  , из уравнений (9) и (10) при
, из уравнений (9) и (10) при  получим
получим

 и
и  в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии
в (9) и (10) получаем уравнения, позволяющие определить ток и напряжение по их значениям в конце линии ;
;
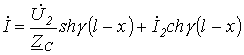 .
.
 ;
; .
. ;
;  и
и  ; при этом условие
; при этом условие 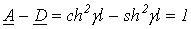 выполняется.
выполняется. и
и  , откуда входное сопротивление
, откуда входное сопротивление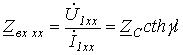 .
.
 и
и 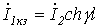 . Следовательно,
. Следовательно, .
.

 ,
, .
.
 и
и 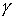 линии, по которым затем могут быть рассчитаны ее первичные параметры
линии, по которым затем могут быть рассчитаны ее первичные параметры 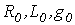 и
и  .
.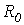 и
и 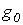 равны нулю. В этом случае, как было показано ранее,
равны нулю. В этом случае, как было показано ранее,  и
и  . Таким образом,
. Таким образом,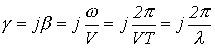 ,
, .
.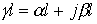 :
: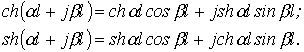
 и
и  .
. ;
;
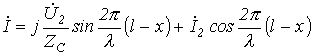 .
.
 и
и  , что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
, что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).


