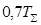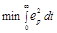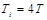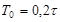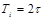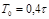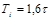Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет настроек регулятора по КопеловичуСодержание книги
Поиск на нашем сайте
Расшифровка методов
Расчет настроек регулятора методом Куна (нормальная настройка) Расчет настроек регулятора методом Куна (быстрая настройка)
Расчет настроек регулятора по Копеловичу
объект с самовыравниванием
Объект без самовыравнивания
Формулы метода ВТИ (Всесоюзный технологический институт)
5. Автоколебания в САР. Определение параметров автоколебаний с помощью графических построений. В нелинейных САР возможны собственные колебания с постоянной амплитудой частотой при отсутствии внешних колебательных воздействий. Эти колебания могут быть устойчивыми и неустойчивыми. Устойчивые собственные колебания с постоянной амплитудой и частотой при отсутствии внешних колебательных воздействий называются автоколебаниями. Удобно рассматривать эти собственные колебания, привлекая фазовую плоскость, по осям которой откладываются координаты х – отклонение выходной переменной системы от установившегося значения и
Жирной линией на фазовой плоскости обозначены особые линии – для а) устойчивого, б) неустойчивого предельного циклов. Предельные циклы разграничивают области начальных условий, для которых фазовые траектории носят качественно разный характер. Так, для а), фазовые траектории для начальных условий, находящихся внутри предельного цикла, раскручиваются от положения равновесия Если в системе установились гармонические автоколебания, то На фазовой плоскости значения амплитуды и частоты автоколебаний непосредственно не просматриваются. Однако, их можно определить приблизительно, исходя из рассмотрения предельного цикла. Если предельный цикл не является эталоном, то автоколебания не будут гармоническими колебаниями. Если, однако, положить, что автоколебания будут близки к гармоническим, то из картинки предельного цикла а) имеем
По модели данных Примеры: -Иерархические -Сетевые -Реляционные -Объектно-ориентированные -Объектно-реляционные По степени распределённости · Локальные СУБД (все части локальной СУБД размещаются на одном компьютере) · Распределённые СУБД (части СУБД могут размещаться на двух и более компьютерах). По способу доступа к БД · Файл-серверные В файл-серверных СУБД файлы данных располагаются централизованно на файл-сервере. СУБД располагается на каждом клиентском компьютере (рабочей станции). Доступ СУБД к данным осуществляется через локальную сеть. Синхронизация чтений и обновлений осуществляется посредством файловых блокировок. Преимуществом этой архитектуры является низкая нагрузка на процессор файлового сервера. Недостатки: потенциально высокая загрузка локальной сети; затруднённость или невозможность централизованного управления; затруднённость или невозможность обеспечения таких важных характеристик как высокая надёжность, высокая доступность и высокая безопасность. Применяются чаще всего в локальных приложениях, которые используют функции управления БД; в системах с низкой интенсивностью обработки данных и низкими пиковыми нагрузками на БД. На данный момент файл-серверная технология считается устаревшей, а её использование в крупных информационных системах — недостатком[2]. Примеры: Microsoft Access, Paradox, dBase, FoxPro, Visual FoxPro. · Клиент-серверные Клиент-серверная СУБД располагается на сервере вместе с БД и осуществляет доступ к БД непосредственно, в монопольном режиме. Все клиентские запросы на обработку данных обрабатываются клиент-серверной СУБД централизованно. Недостаток клиент-серверных СУБД состоит в повышенных требованиях к серверу. Достоинства: потенциально более низкая загрузка локальной сети; удобство централизованного управления; удобство обеспечения таких важных характеристик как высокая надёжность, высокая доступность и высокая безопасность. Примеры: Oracle, Firebird, Interbase, IBM DB2, Informix, MS SQL Server, Sybase Adaptive Server Enterprise, PostgreSQL, MySQL, Caché, ЛИНТЕР. · Встраиваемые Встраиваемая СУБД — СУБД, которая может поставляться как составная часть некоторого программного продукта, не требуя процедуры самостоятельной установки. Встраиваемая СУБД предназначена для локального хранения данных своего приложения и не рассчитана на коллективное использование в сети. Физически встраиваемая СУБД чаще всего реализована в виде подключаемой библиотеки. Доступ к данным со стороны приложения может происходить через SQL либо через специальные программные интерфейсы. Примеры: OpenEdge, SQLite, BerkeleyDB, Firebird Embedded, Microsoft SQL Server Compact, ЛИНТЕР.
7. Оценка качества САР по временным характеристикам. Любая САР для того, чтобы удовлетворять своему назначению, как уже отмечалось выше, прежде всего должна быть устойчивой. Однако устойчивость является необходимым, но не достаточным условием технической прочности системы регулирования. Помимо устойчивости, к переходному процессу предъявляются требования, обуславливающие его так называемые качественные показатели. Под качеством системы понимают некоторые свойства кривой ее переходного процесса. Чаще всего рассматривают переходный процесс по управляющему воздействию.
Рис.V.1. Структурная схема САР Здесь W(p) – передаточная функция САР, x(t) – входное управляющее воздействие, z(t) – выходной сигнал. В качестве управляющего сигнала может быть использован сигнал любого вида, но чаще всего применяется толчкообразный (скачкообразный) сигнал с величиной скачка, равной либо единице, как при получении переходной характеристики системы, либо произвольной величине. Если система обладает колебательными свойствами, то выходной сигнал по управляющему (скачкообразному) сигналу качественно будет выглядеть примерно так, как изображено на рис.V.2. Из показателей качества (еще говорят: прямых оценок качества регулирования) обычно рассматривают: 1. Установившееся значение выходного сигнала
Рис.V. 2. Переходный процесс в САР 2. Точность регулирования Δ – заданная малая постоянная величина, представляющая собой обычно допустимую ошибку. Для входного единичного скачка для технических систем, как правило, Δ = (1÷ 5) %. 3. Время регулирования tр (время переходного процесса). Выходной сигнал z(t) и его установившееся значение zуст становятся неразличимы с точностью до величины Δ после времени tp, когда сигнал z(t) войдет последний раз в коридор двойной точности 2Δzуст и больше никогда из него не выйдет. Таким образом, величина tp определяется как время, протекающее от момента приложения входного скачка до момента, после которого имеет место неравенство: 4. Под перерегулированием σ обычно понимают максимальный относительный выброс регулируемого сигнала z(t) = zmax от его установившегося значения zуст, выраженный в процентах Для большинства промышленных систем σ = (10-40)%. Здесь были перечислены наиболее часто встречающиеся показатели качества регулирования. Кроме того, для отдельных систем используются и другие показатели, например, 5. Порядок астатизма системы ν. 6. Время tмах наступления максимального значения регулируемой 7. величиныzmax. 8. Время t1 первого пересечения кривой переходного процесса установившегося значения zуст (характеризует производную zуст (t)). 9. Количество колебаний переходного процесса за время tp и др.
8. Представление импульсного элемента при исследовании импульсных САР.
9. Синтез САР оптимальной по быстродействию. Функционал имеет вид
Обозначим верхнюю границу Гамильтониана
Если точная верхняя граница достигается, то это соответствует мах гамильтониана Для рассматриваемого случая
С учетом принятых обозначений, основная теорема ПМ САР оптимальных по быстродействию формулируется следующим образом: Пусть 1. Для всех
2. в конечные моменты времени Как и в общем случае, если функция Поэтому проверку условия (7) можно производить в любой момент времени на интервале Замечание: т.к. для большинства случаев
Объект представляет собой 2 последовательности соединенных интегрирующих звена
III Выбор СУБД При выборе СУБД руководствуются следующими соображениями: - аппаратное обеспечение, на котором в дальнейшем будет работать проектируемая база данных; - системное программное обеспечение, с которым будет в последствии работать проектируемая база данных и соответствующее ей приложения; - методология и подходы, к программированию реализованные в той или иной СУБД; - модель данных, которая встроена в конкретную СУБД; Выбор СУБД полностью определяется на II этапе построения базы данных, т. к. оно зависит от той модели данных, которая встроена в выбранную СУБД. V Физическое проектирование На этом этапе необходимо на конкретной СУБД, которую выбрали ранее, реализовать базу данных по той информации, которую собрали, обработали и подготовили (на предыдущих этапах проектирования базы данных). Описываются модули, их назначение, а также структура модулей
Расшифровка методов Расчет настроек регулятора методом Куна (нормальная настройка) Расчет настроек регулятора методом Куна (быстрая настройка)
Расшифровка методов
Расчет настроек регулятора методом Куна (нормальная настройка) Расчет настроек регулятора методом Куна (быстрая настройка)
Расчет настроек регулятора по Копеловичу
объект с самовыравниванием
Объект без самовыравнивания
Формулы метода ВТИ (Всесоюзный технологический институт)
5. Автоколебания в САР. Определение параметров автоколебаний с помощью графических построений. В нелинейных САР возможны собственные колебания с постоянной амплитудой частотой при отсутствии внешних колебательных воздействий. Эти колебания могут быть устойчивыми и неустойчивыми. Устойчивые собственные колебания с постоянной амплитудой и частотой при отсутствии внешних колебательных воздействий называются автоколебаниями. Удобно рассматривать эти собственные колебания, привлекая фазовую плоскость, по осям которой откладываются координаты х – отклонение выходной переменной системы от установившегося значения и
Жирной линией на фазовой плоскости обозначены особые линии – для а) устойчивого, б) неустойчивого предельного циклов. Предельные циклы разграничивают области начальных условий, для которых фазовые траектории носят качественно разный характер. Так, для а), фазовые траектории для начальных условий, находящихся внутри предельного цикла, раскручиваются от положения равновесия Если в системе установились гармонические автоколебания, то На фазовой плоскости значения амплитуды и частоты автоколебаний непосредственно не просматриваются. Однако, их можно определить приблизительно, исходя из рассмотрения предельного цикла. Если предельный цикл не является эталоном, то автоколебания не будут гармоническими колебаниями. Если, однако, положить, что автоколебания будут близки к гармоническим, то из картинки предельного цикла а) имеем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1022; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.012 с.) |

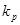






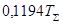


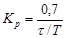
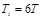





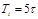

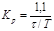
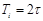
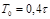
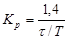


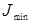

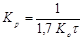


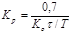



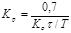
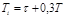
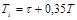

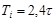


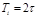

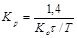
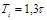












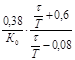
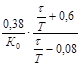
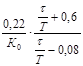

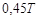
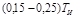






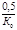

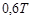
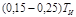
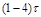


 - скорость изменения этого отклонения.
- скорость изменения этого отклонения.
 до предельного цикла, а для начальных условий, находящихся вне предельного цикла, - скручиваются извне до предельного цикла. Значит, в такой нелинейной системе нет состояния устойчивого равновесия, а есть режим автоколебаний. Для случая б) картина противоположная, здесь для области начальных условий, расположенных внутри предельного цикла, имеет местоположение устойчивого равновесия в начале координат, а предельный цикл характеризует неустойчивые собственные колебания.
до предельного цикла, а для начальных условий, находящихся вне предельного цикла, - скручиваются извне до предельного цикла. Значит, в такой нелинейной системе нет состояния устойчивого равновесия, а есть режим автоколебаний. Для случая б) картина противоположная, здесь для области начальных условий, расположенных внутри предельного цикла, имеет местоположение устойчивого равновесия в начале координат, а предельный цикл характеризует неустойчивые собственные колебания. где А – амплитуда, а ω – частица гармонических колебаний. Максимальные значения для х будет при
где А – амплитуда, а ω – частица гармонических колебаний. Максимальные значения для х будет при 
 Сравнивая (1) и (3), (2) и (4) имеем для амплитуды и частоты автоколебаний:
Сравнивая (1) и (3), (2) и (4) имеем для амплитуды и частоты автоколебаний: 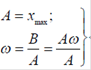



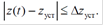


 Гамильтонион с учетом (1)
Гамильтонион с учетом (1) Рассмотрим n-мерный вектор
Рассмотрим n-мерный вектор 

 Тогда система уравнений и сопряженная система принимает следующий вид
Тогда система уравнений и сопряженная система принимает следующий вид 


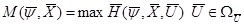
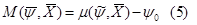 т.к.
т.к.  , то
, то 
 при
при  некоторое допустимое управление, переводящее изображение в точку и соответствующее
некоторое допустимое управление, переводящее изображение в точку и соответствующее  , а
, а  -- соответствующее этому управлению траектория. Для оптимальности по быстродействию управления
-- соответствующее этому управлению траектория. Для оптимальности по быстродействию управления  , удовлетворяющей системе уравнений (4) и что:
, удовлетворяющей системе уравнений (4) и что: функция
функция  т.е.
т.е. =
=  ; (6)
; (6) выполняется соотношение
выполняется соотношение 
 удовлетворяют выражению (4) и условию (6), то функция
удовлетворяют выражению (4) и условию (6), то функция  постоянна.
постоянна. .
.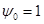 то из выражения
то из выражения  и выражения (5) следует, что вдоль оптимальной траектории гамильтониана
и выражения (5) следует, что вдоль оптимальной траектории гамильтониана