Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Емкость уединенного проводникаСодержание книги
Поиск на нашем сайте
Емкость уединенного проводника, т.е. проводника, бесконечно удаленного от всех остальных проводников, определяется величиной заряда, который нужно сообщить проводнику, чтобы его потенциал был равен единице. При этом предполагается, что аддитивная постоянная в выражении для потенциала выбрана так, что
Емкость уединенного шара: потенциал на расстоянии Но по определению В системе СИ единица измерения емкости – фарада: 1Ф= 1мкФ=9×105см, 1 пФ=0.9 см. Емкость Земли:
Неуединенный проводник Его потенциал при сообщении ему определенного заряда существенно зависит от формы и расположения других проводников. Поле заряженного проводника вызывает перераспределение зарядов на других близко расположенных проводниках – в том числе и на незаряженных (явление электростатической индукции). По достижении равновесия заряды на проводниках распределятся таким образом, что внутри каждого проводника сумма полей, созданных индуцирующим зарядом и индуцированным зарядом, была бы равна нулю.
Две бесконечные параллельные металлические плоскости
1) Вблизи металлической плоскости существует только нормальная компонента поля Если имеем пластины конечных размеров, то результат почти тот же, но имеются незначительные отклонения на краях пластин. Плотность поверхностных зарядов
РИС.15-5
Поле между пластинами Зададим расстояние между пластинами
Вообще говоря, расчет электростатического потенциала требует знания распределения объемной плотности заряда в исследуемом пространстве. Если задано В электродинамике доказывается теорема единственности: если удалось найти (чаще всего – просто угадать) функцию
Метод электрических изображений Решение задач электростатики облегчается некоторыми искуственными приемами, в частности, методом электрических изображений.
РИС.15-6 Эквипотенциаль
Сначала вычислили потенциал данной системы точечных зарядов и провели некоторую эквипотенциальную поверхность В результате мы получаем решение сразу двух задач. В полупространстве I по одну сторону проводящего тела Однако в силу теоремы единственности поле индуцированных зарядов в полупространстве I эквивалентно полю, создаваемому зарядами Совокупность этих зарядов называется электрическим изображением зарядов
Пример. Точечный заряд над бесконечной проводящей плоскостью РИС.15-7
РИС.15-8
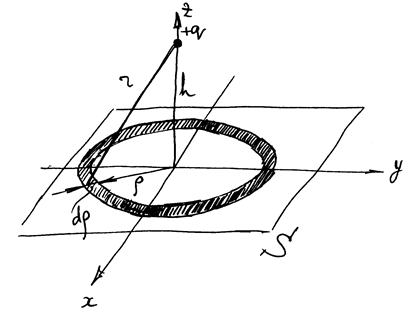
При таком задании потенциала он обращается в нуль на плоскости Теперь начинаем вычислять поверхностную плотность индуцированного заряда (Рис. 15-8) Осевая симметрия относительно оси
РИС.15-9
Проверка: полный индуцированный на поверхности заряд должен быть равен
{новая переменная =
Энергия взаимодействия электрических зарядов
При перемещении электрических зарядов силы кулоновского взаимодействия между ними производят некоторую работу
Система электрических зарядов обладает потенциальной энергией.
РИС.15-10
Пусть имеется неподвижно закрепленный заряд +q. Если заряд –q отпустить, то он начнет двигаться в сторону заряда Итак, неподвижно закреплен заряд
РИС.15-11
Заряд
Энергию взаимодействия двух точечных зарядов можно записать в симметричной форме:
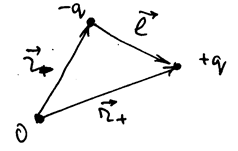
Собираем систему из трех зарядов
РИС.15-12
В поле заряда
В систему зарядов
Полная энергия взаимодействия системы трех зарядов:
Вообще Потенциальная энергия взаимодействия
Обобщаем полученные результаты на систему объемных и поверхностных зарядов. Разделяя объемные заряды на элементарные
Несколько простых примеров 1) Энергия уединенного проводника
Пусть проводник изолирован от земли и совсем не заряжен: 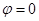 . Затем зарядим до q0. . Затем зарядим до q0. 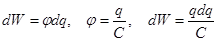 , ,  {заряжаем до уровня {заряжаем до уровня  , , 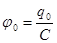 }= }=
= РИС.15-13
2)
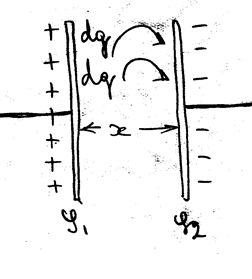
Энергия плоского конденсатора РИС.15-14
Понятие о плотности энергии
Рассмотрим простейший случай плоского конденсатора.
Этот результат имеет на самом деле весьма общее значение. Можно показать:
Носителем энергии является электрическое поле, энергия локализована в пространстве так, что в единице объема содержится
Математическое отступление (теорема Грина) (дополнительный материал)
Обозначим вектор
Подставим полученный результат в формулу, выражающую теорему Гаусса:
Другая форма записи. Можно взять
Вычитая, получим:
Здесь
Теперь рассмотрим интересующий нас случай энергии взаимодействия:
Положим в теореме Грина
Вспоминаем: 1)
2) Подставляя, получаем:
Поверхность (т. е. заряженные поверхности). Полагаем, что разрыва потенциала не происходит (т.е. по обе стороны заряженной поверхности Тогда, стягивая поверхность
где ранее Тогда Итак, при стягивании
Соберем теперь полученные результаты.
Делим на
Распространим теперь интегрирование по области, где существуют объемные и поверхностные заряды, но и по всей области, где существует поле всех этих зарядов. Это означает, что нужно найти такую поверхность, на которой (во всех точках которой) напряженность поля В действительности такой замкнутой оболочки, как правило, не существует, и граница поля На самом деле нас интересует обращение в нуль некоторых конкретных величин на так называемой границе поля. Обычно интегрируют по бесконечному пространству, но это можно делать в том и только в том случае, если интегралы всех интересующих нас величин по поверхности Если В нашем случае
В дальнейшем будем полагать, что по определению понятия полного поля интегралы по ограничивающей полное поле поверхности Итак:
Итак, носителем энергии является электрическое поле, энергия локализована в пространстве так, что в единице объема содержится:
Математическое отступление окончилось.
Появилась некоторая проблема. Если мы имеем один точечный заряд, то создаваемое им поле Если воспользоваться формулой Дело в том, что формула Собственная энергия заряда – это работа сил взаимного отталкивания, которую они произвели бы, если бы все части заряда разлетелись на
Полная энергия двух зарядов
Из Следовательно,
Энергия электрического поля не обладает свойством аддитивности:
Пондеромоторные силы (дополнительный материал) Напряженность поля Значит Механическая сила, действующая на точечный заряд
Сила, действующая на поверхностные заряды
Заряженный мыльный пузырь-пример уединенной напряженной поверхности. Между элементами заряда действуют силы отталкивания. Только силы, растягивающие поверхность. Мыльный пузырь растягивается, до тех пор, пока силы отталкивания не уравновесятся силами поверхностного натяжения и разностью давлений воздуха внутри и вне пузыря. Итак, в случае уединенного проводника все электрические силы сводятся лишь к взаимному отталкиванию элементов заряда этого проводника. Какие силы будут приложены к поверхности неуединенного проводника в произвольном электростатическом поле? Представим заряженную сферу с поверхностью S.Напряженность поля с внешней стороны элемента dS:
Поле В двух смежных точках, лежащих по обе стороны поверхности Значит, с внешней стороны поверхности
С внутренней стороны поверхности:
Отсюда: Сила, испытываемая зарядом Сила, действующая на единицу площади заряженного проводника:
Сила, действующая на диполь
Если электрическое поле однородно, Однако на диполь действует момент сил Отсюда вывод: диполь стремится повернуться в электрическом поле так, чтобы его момент был параллелен (антипараллелен, но это положение не устойчиво) полю E. Если электрическое поле неоднородно, то Для точечного диполя
Сила: Скалярное произведение: В этих обозначениях Эта сила направлена в сторону возрастания электрического поля: диполь втягивается в область сильного поля.
Другая формулировка для пондеромоторных сил, из выражения для энергии
Сила, действующая на пластины плоского конденсатора.
Или:
Сила, создаваемая поверхностным зарядом:
Вопрос об устойчивости электрических систем. Теорема Ирншоу (дополнительный материал)
Для электрической теории строения материи весьма важен вопрос о возможности существования устойчивых конфигураций электрических зарядов (электронов и протонов). Может ли эта система находиться в статическом равновесии или же в атомах и молекулах эти частицы должны находиться в непрерывном движении? Как это выяснить? Электрическая энергия играет роль потенциальной энергии – в этом мы уже убедились. Условие устойчивости любой системы – нахождение ее в состоянии минимума потенциальной энергии - ищем
Условия min: 1) 2)
Если
Это можно показать: Принимаем точку P за начало координат. Тогда
Отсюда:
Из изложенного следует, что статическая система электрических зарядов не является устойчивой. Физический смысл: разноименные заряды притягиваются вплоть до взаимного уничтожения, а одноименные отталкиваются вплоть до удаления в бесконечность.
Общая мораль: 1) атом должен представлять собой динамическую систему; 2) поскольку теорема Ирншоу исходит только из одного обстоятельства – сила взаимодействия
Статическая система, которую мы здесь рассматривали, может быть устойчивой лишь при наличии дополнительных сил неэлектрического происхождения.
16 Основные итоги, касающиеся электростатики в вакууме
Из (1) и (3) мы легко получили уравнение Пуассона:
Затем было введено представление о потенциальной энергии взаимодействия точечных зарядов, которую мы представляем в симметричной форме:
Полученные результаты можно обобщить на случай объемных и поверхностных зарядов. Если разбить эти заряды на элементарные
Воспользовавшись теоремой Грина
или
(где
Поиски минимума потенциальной энергии взаимодействия Физический смысл: разноименные заряды притягиваются вплоть до взаимного уничтожения, а одноименные отталкиваются вплоть до удаления в бесконечность. Следовательно: 1) атом должен представлять собой динамическую систему, в которой действуют силы неэлектрического происхождения; 2) любая система, где действуют только силы
ДИЭЛЕКТРИКИ Введение Диэлектрики – в отличие от металлов и полупроводников – не имеют свободных носителей заряда, свободных – чтобы перемещаться под действием электрического поля. Два главных типа диэлектриков. 1) Молекулярные диэлектрики. Вещество состоит из нейтральных молекул – это жидкие, аморфные и газообразные вещества, молекулярные кристаллы, в том числе жидкие кристаллы. Вещество в целом нейтрально. В зависимости от типа молекул молекулярные диэлектрики подразделяются на два класса: а) неполярные, электрический момент каждой молекулы равен нулю, б) полярные, электрический момент каждой молекулы не равен нулю, 2) Ионные диэлектрики (например, NaCl). Вещество нейтрально в целом, нейтральна каждая элементарная ячейка. Положительные и отрицательные заряды достаточно жестко закреплены в положениях равновесия. Заряды - в диэлектриках обоих типов – не могут под действием внешнего электрического поля перемещаться таким образом, чтобы приобрести конечную скорость направленного движения (дрейф), они могут лишь немного сместиться из положения равновесия (в ионных кристаллах и в молекулярных неполярных), при этом в каждой молекуле возникает Поэтому с формальной точки зрения можно обе разновидности диэлектриков (в целом нейтральных диэлектриков,
РИС.16-1
Вычислим вектор электрической поляризации системы, состоящей из двух точечных зарядов 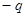 и и  . .
РИС.16-2
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 416; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.0.57 (0.013 с.) |

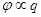 Þ
Þ 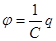 ;
; 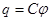 .
.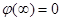 .
. .
.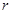 от металлического заряженного шара
от металлического заряженного шара 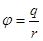 . На поверхности шара (и в любой другой точке шара)
. На поверхности шара (и в любой другой точке шара) 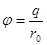 .
.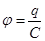 . Отсюда
. Отсюда 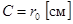 .
.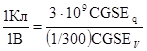 =9×1011см;
=9×1011см; 6×103км=6×108см<1мФ.
6×103км=6×108см<1мФ.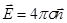 . где
. где 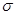 - поверхностная плотность зарядов.
- поверхностная плотность зарядов.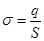 , где
, где 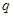 - заряд одной из пластин.
- заряд одной из пластин.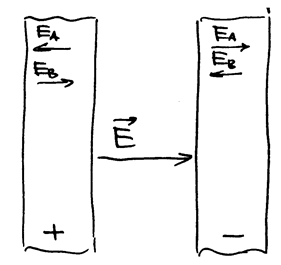
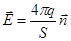 .
.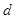 и вычислим потенциал:
и вычислим потенциал: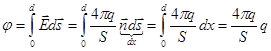 . Отсюда:
. Отсюда:  - емкость плоского конденсатора.
- емкость плоского конденсатора. , то из уравнения Пуассона
, то из уравнения Пуассона 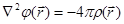 можно найти
можно найти 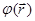 при соответствующих граничных условиях (с точностью до аддитивной постоянной).
при соответствующих граничных условиях (с точностью до аддитивной постоянной).
 разделяет все пространство на два полупространства I и I’.
разделяет все пространство на два полупространства I и I’. - заряды в полупространстве I,
- заряды в полупространстве I, - заряды в полупространстве I’.
- заряды в полупространстве I’.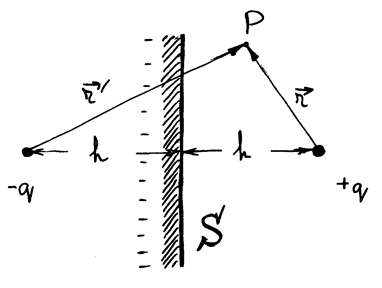
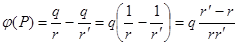 .
. ), следовательно,
), следовательно, 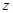 .
. 
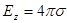 ,
, ,
, 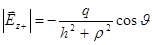 .
.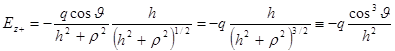 ;
; ,
,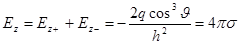 Þ
Þ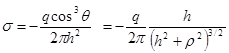 .
.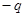 . Убеждаемся в этом путем непосредственного интегрирования.
. Убеждаемся в этом путем непосредственного интегрирования.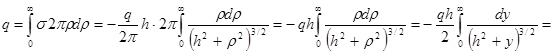
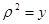 ,
, 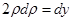 }
}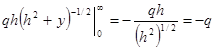 - к чему и стремились.
- к чему и стремились. . Эта работа происходит за счет убыли энергии взаимодействия между зарядами:
. Эта работа происходит за счет убыли энергии взаимодействия между зарядами: , где
, где  - электрическая энергия.
- электрическая энергия.
 . Вычислим потенциальную энергию взаимодействия двух точечных зарядов при условии, что
. Вычислим потенциальную энергию взаимодействия двух точечных зарядов при условии, что  .
.
 приносим из
приносим из  в поле заряда
в поле заряда 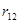 . При этом совершается работа
. При этом совершается работа  . Здесь
. Здесь  - потенциал, создаваемый зарядом
- потенциал, создаваемый зарядом  . Если теперь вносим из
. Если теперь вносим из 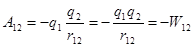 ;
; ,
, 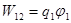 ,
, 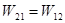 .
. .
.
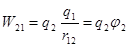 .
. вносим заряд
вносим заряд 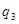 :
: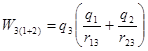 .
.
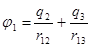 - потенциал, создаваемый зарядами
- потенциал, создаваемый зарядами  - потенциал, создаваемый в точке, где находится заряд
- потенциал, создаваемый в точке, где находится заряд 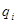 , всеми остальными зарядами.
, всеми остальными зарядами.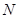 зарядов:
зарядов: .
.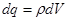 и поверхностные на элементарные
и поверхностные на элементарные  , получаем:
, получаем: , где
, где  - значение потенциала поля всех объемных и поверхностных зарядов в элементе объема
- значение потенциала поля всех объемных и поверхностных зарядов в элементе объема 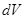 или на элементе поверхности
или на элементе поверхности 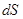 .
.
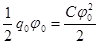 .
.
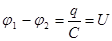 ,
,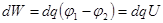 ,
, 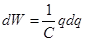 ,
, 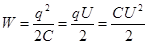 - конденсатор запасает энергию.
- конденсатор запасает энергию.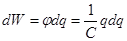 Þ
Þ 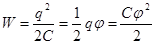 .
.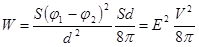 .
. (это получается из
(это получается из  - объемная плотность электрической энергии.
- объемная плотность электрической энергии. .
. как произведение некоторого скаляра на градиент другого скаляра (
как произведение некоторого скаляра на градиент другого скаляра ( - некоторые функции координат, непрерывные, конечные, имеющие производные первого и второго порядков).
- некоторые функции координат, непрерывные, конечные, имеющие производные первого и второго порядков).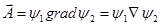 ;
;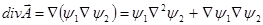 ;
;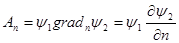 .
.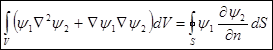 - теорема Грина.
- теорема Грина.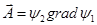 . Получим:
. Получим: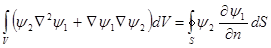 .
. .
. - любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков.
- любые непрерывные конечные скалярные функции координат, обладающие в области интегрирования производными первого и второго порядков.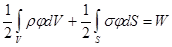 .
. .
. .
.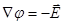 ,
,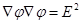 ;
; .
.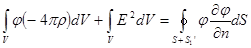 .
. выделяет из объема могущие лежать в нем поверхности разрыва
выделяет из объема могущие лежать в нем поверхности разрыва 
 ).
).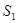 , получим:
, получим: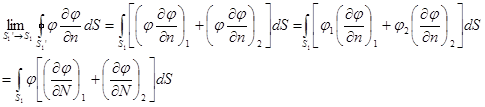
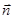 - общая нормаль для
- общая нормаль для 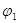 и
и 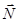 - некая новая нормаль, внешняя по отношению к заряженной поверхности.
- некая новая нормаль, внешняя по отношению к заряженной поверхности.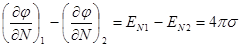 .
. .
. .
.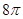 :
: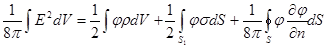 .
. обращается в 0.
обращается в 0.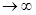 .
. . Следовательно, подинтегральные выражения в интересующих нас поверхностных интегралах должны убывать быстрее, чем
. Следовательно, подинтегральные выражения в интересующих нас поверхностных интегралах должны убывать быстрее, чем 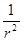 при
при  .
.
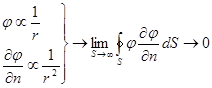 .
. .
.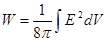 - это бесконечная сумма слагаемых вида
- это бесконечная сумма слагаемых вида 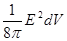 .
.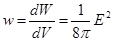 - объемная плотность электрической энергии.
- объемная плотность электрической энергии.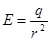 и
и  .
. , то получим
, то получим 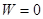 , так как других зарядов, кроме
, так как других зарядов, кроме 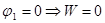 .
. и посчитали бы его энергию по формуле
и посчитали бы его энергию по формуле 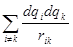 , то получили бы его собственную энергию
, то получили бы его собственную энергию 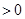 .
.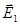 - поле заряда №1,
- поле заряда №1,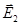 - поле заряда №2,
- поле заряда №2,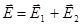 .
.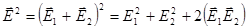 .
. ;
;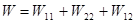 (
( - собственные энергии,
- собственные энергии,  - энергия взаимодействия).
- энергия взаимодействия).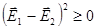 следует, что
следует, что  .
.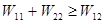 , т.е положительная собственная энергия зарядов всегда больше (или равна) взаимной энергии зарядов, которая может быть как положительной, так и отрицательной. Значит, при всех возможных перемещениях зарядов, не меняющих размеры и формы,
, т.е положительная собственная энергия зарядов всегда больше (или равна) взаимной энергии зарядов, которая может быть как положительной, так и отрицательной. Значит, при всех возможных перемещениях зарядов, не меняющих размеры и формы, 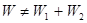 !
! - сила, действующая на единичный положительный пробный заряд.
- сила, действующая на единичный положительный пробный заряд.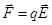 .
. , и из поля всех остальных зарядов
, и из поля всех остальных зарядов 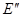 .
. будет в этих же точках одинаковым по величине, но противоположным по направлению.
будет в этих же точках одинаковым по величине, но противоположным по направлению. .
. .
.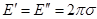 .
.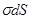 элемента
элемента 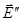 всех прочих зарядов:
всех прочих зарядов: 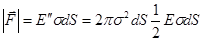 .
.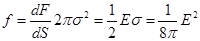 - поверхностная плотность пондеромоторных сил.
- поверхностная плотность пондеромоторных сил.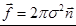 ,
,  .
. и равнодействующая
и равнодействующая 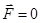 .
.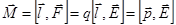 .
.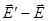 (приращение поля на отрезке
(приращение поля на отрезке  , равном плечу диполя):
, равном плечу диполя):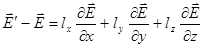 .
. .
.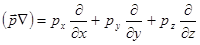 .
.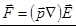 .
.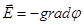 ,
,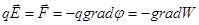 .
. .
. ,
,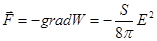 .
.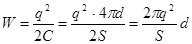 ,
,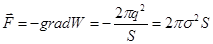 .
.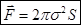 - в полном согласии с полученным ранее результатом:
- в полном согласии с полученным ранее результатом: 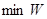 .
.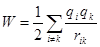 ,
,  .
. ; {
; {  - координата любого заряда}
- координата любого заряда}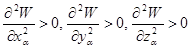 , или
, или 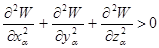 , так как min не достигается, если хотя бы одна из вторых производных
, так как min не достигается, если хотя бы одна из вторых производных 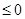 .
.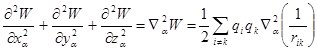 .
.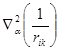 =0, если
=0, если  .
. или
или 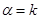 , то
, то 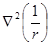 = 0 в любой точке P.
= 0 в любой точке P.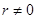 ).
).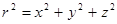 ,
,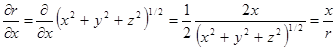 .
.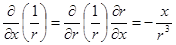 ;
;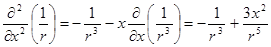 .
.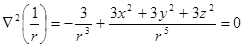 - что и требовалось доказать.
- что и требовалось доказать.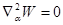 - потенциальная энергия не имеет минимума, следовательно (теорема Ирншоу):
- потенциальная энергия не имеет минимума, следовательно (теорема Ирншоу):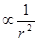 , значит, устойчивость нашей планетной системы обусловливается лишь движением планет.
, значит, устойчивость нашей планетной системы обусловливается лишь движением планет.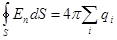
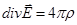

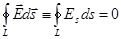
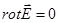
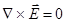


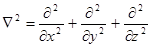 , которое в отсутствие объемных зарядов переходит в уравнение Лапласа
, которое в отсутствие объемных зарядов переходит в уравнение Лапласа  . Уравнение Пуассона было решено для некоторых частных случаев.
. Уравнение Пуассона было решено для некоторых частных случаев. ,
, 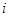 -го заряда.
-го заряда.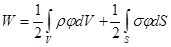 , где
, где 
 ;
; , но в достаточно большом объеме
, но в достаточно большом объеме 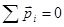 .
.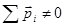 , или могут повернуться так (в полярных диэлектриках), чтобы
, или могут повернуться так (в полярных диэлектриках), чтобы 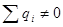 ) описывать вектором электрической поляризации системы
) описывать вектором электрической поляризации системы  , где суммирование производится по всем электронам и ядрам системы и
, где суммирование производится по всем электронам и ядрам системы и 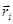 - это радиус-вектор, проведенный к заряду
- это радиус-вектор, проведенный к заряду 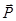 .
.
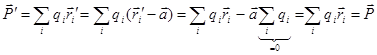 .
.