Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электрический заряд.Плотность заряда.Закон Кулона.Содержание книги
Поиск на нашем сайте
Напряженность электрического поля. Заряды, находясь на некотором расстоянии один от другого, взаимодействуют. Это взаимодействие осуществляется посредством электрического поля, которое материально, существует независимо от нас и обладает определенными свойствами и характеристиками. Напряженность электрического поля— силовая характеристика электрического поля, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля. Другая формулировка: отношение силы Напряженность — векторная величина. С другой стороны, сила, действующая на заряд q со стороны электрического поля, равна
Густота силовых линий больше вблизи заряженных тел, где напряженность поля также больше. Напряженность электрического поля Однородное электрическое поле— это поле, напряженность которого одинакова во всех точках пространства. По закону Кулона заряд будет действовать на другой заряд с силой Линии напряженности никогда не пересекаются, поскольку в каждой данной точке пространства вектор
В случае однородного поля (для него вектор напряженности в любой точке постоянен по модулю и направлению) линии напряженности параллельны вектору напряженности. Принцип суперпозиции. Если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых
Линии напряженности. Электрическое поле изображают с помощью силовых линий. Силовые линии указывают направление силы, действующей на положительный заряд в данной точке поля.
Свойства силовых линий электрического поля · Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных. · Силовые линии электрического поля всегда перпендикулярны поверхности проводника. · Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным (если силовые линии параллельны) и неоднородным (если силовые линии не параллельны). Поток вектора напряженности электрического поля. Теорема Гаусса Как и для любого векторного поля важно рассмотреть свойства потока электрического поля. Поток электрического поля определяется традиционно. Выделим малую площадку площадью ΔS, ориентация которой задается единичным вектором нормали
В пределах малой площадки электрическое поле можно считать однородным, тогда поток вектора напряженности ΔФE определяется как произведение площади площадки на нормальную составляющую вектора напряженности
где
В произвольном электростатическом поле поток вектора напряженности через произвольную поверхность, определяется следующим образом (рис. 158): - поверхность разбивается на малые площадки ΔS (которые можно считать плоскими); - определяется вектор напряженности на этой площадке (который в пределах площадки можно считать постоянным); - вычисляется сумма потоков через все площадки, на которые разбита поверхность. Эта сумма называется потоком вектора напряженности электрического поля через заданную поверхность.
Теорема Гаусса в вакууме. Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
· · · Данное выражение представляет собой теорему Гаусса в интегральной форме. · Замечание: поток вектора напряжённости через поверхность не зависит от распределения заряда (расположения зарядов) внутри поверхности. В дифференциальной форме теорема Гаусса выражается следующим образом:
Здесь · Теорема Гаусса может быть доказана как теорема в электростатике исходя из закона Кулона. Формула однако также верна в электродинамике, хотя в ней она чаще всего не выступает в качестве доказываемой теоремы, а выступает в качестве постулируемого уравнения (в этом смысле и контексте ее логичнее называть законом Гаусса.
Понятие о потенциале. Разность потенциалов. Определение потенциала, как и потенциальной энергии, является в подавляющем большинстве случаев промежуточным действием. Как правило, практическое значение имеет определение работы, которую выполняет электрическое поле. Связанный непосредственно с потенциальной энергией, потенциал может быть определен лишь с точностью до определенной постоянной величины, значение которой зависит от выбора нулевого уровня отсчета. Значение потенциала определяется с точностью до некоторой постоянной величины. Потенциал точки поля определяется по напряженности электрического поля E и расстоянию ее от нулевого уровня l. φ = El. Работа в электростатическом поле определяется однозначно. Если выбор нулевого уровня произвольный, то и значение l может быть произвольным. Поэтому часто потенциал записывают в виде φ = El + C, С — константа. Если же определять работу, которая по определению равна изменению потенциальной энергии с противоположным знаком, то получается вполне определенная величина: A = qEl1 + C — qEl2 — C = qEl1 — qEl2. Полученное выражение можно записать в виде A = q(φ1 — φ2) = qΔφ. Отсюда Δφ = φ1 — φ2 = A / q. однозначно, то и разность потенциалов будет иметь вполне определенное значение. Поэтому разность потенциалов считают отдельной физической величиной. Физическая величина, характеризующая энергетическое состояние поля и равная отношению работы по перемещению заряженного тела из одной точки поля в другую к значению заряда, называется разностью потенциалов. Разность потенциалов в электростатическом поле определяется однозначно. Для измерения разности потенциалов, как и потенциала, применяется единица 1 вольт и производные от него единицы: 1 мВ, 1 мкВ, 1 кВ, 1 MB. Прибор, которым измеряют разность потенциалов, называется вольтметром. Из предыдущего известно, что разность потенциалов в однородном поле связана с напряженностью электрического поля: φ1 — φ2 = E(l1 — l2). Материал с сайта http://worldofschool.ru Отсюда E = (φ1 — φ2) / (l1 — l2) = Δφ / Δl. Последнее выражение использовано для введения единицы напряженности электрического поля. При φ1 — φ2 = 1 В и l1 — l2 = 1 м получим Е = 1 В/м. По разности потенциалов можно определить напряженность электростатического поля.
Электрический ток. Электри́ческий ток — направленное (упорядоченное) движение частиц или квазичастиц — носителей электрического заряда. Такими частицами могут являться: в металлах — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость). Иногда электрическим током называют также ток смещения, возникающий в результате изменения во времени электрического поля. Электрический ток имеет следующие проявления: · нагревание проводников (не происходит в сверхпроводниках); · изменение химического состава проводников (наблюдается преимущественно в электролитах); · создание магнитного поля (проявляется у всех без исключения проводников). Если заряженные частицы движутся внутри макроскопических тел относительно той или иной среды, то такой ток называют электрический ток проводимости. Если движутся макроскопические заряженные тела (например, заряженные капли дождя), то этот ток называют конвекционным. Различают постоянный и переменный электрические токи, а также всевозможные разновидности переменного тока. В таких понятиях часто слово «электрический» опускают. · Постоянный ток — ток, направление и величина которого не меняются во времени. · Переменный ток — электрический ток, изменяющийся во времени. Под переменным током понимают любой ток, не являющийся постоянным. · Периодический ток — электрический ток, мгновенные значения которого повторяются через равные интервалы времени в неизменной последовательности. · Синусоидальный ток — периодический электрический ток, являющийся синусоидальной функцией времени. Среди переменных токов основным является ток, величина которого изменяется по синусоидальному закону. В этом случае потенциал каждого конца проводника изменяется по отношению к потенциалу другого конца проводника попеременно с положительного на отрицательный и наоборот, проходя при этом через все промежуточные потенциалы (включая и нулевой потенциал). В результате возникает ток, непрерывно изменяющий направление: при движении в одном направлении он возрастает, достигая максимума, именуемого амплитудным значением, затем спадает, на какой-то момент становится равным нулю, потом вновь возрастает, но уже в другом направлении и также достигает максимального значения, спадает, чтобы затем вновь пройти через ноль, после чего цикл всех изменений возобновляется. · Квазистационарный ток — «относительно медленно изменяющийся переменный ток, для мгновенных значений которого с достаточной точностью выполняются законы постоянных токов» (БСЭ). Этими законами являются закон Ома, правила Кирхгофа и другие. Квазистационарный ток, так же как и постоянный ток, имеет одинаковую силу тока во всех сечениях неразветвлённой цепи. При расчёте цепей квазистационарного тока из-за возникающей э.д.с. индукции ёмкости и индуктивности учитываются как сосредоточенные параметры. Квазистационарными являются обычные промышленные токи, кроме токов в линиях дальних передач, в которых условие квазистационарности вдоль линии не выполняется. · Ток высокой частоты — переменный ток, (начиная с частоты приблизительно в десятки кГц), для которого становятся значимыми такие явления, как излучение электромагнитных волн и скин-эффект. Кроме того, если длина волны переменного тока становится сравнимой с размерами элементов электрической цепи, то нарушается условие квазистационарности, что требует особых подходов к расчёту и проектированию таких цепей (см. Длинная линия). · Пульсирующий ток — это периодический электрический ток, среднее значение которого за период отлично от нуля[5]. · Однонаправленный ток — это электрический ток, не изменяющий своего направления. Сила и плотность тока Электрический ток имеет количественные характеристики: скалярную — силу тока, и векторную — плотность тока. Сила тока — физическая величина, равная отношению количества заряда {\displaystyle \Delta Q}, прошедшего за некоторое время {\displaystyle \Delta t} Сила тока в Международной системе единиц (СИ) измеряется в амперах (русское обозначение: А). По закону Ома сила тока {\displaystyle I} Если на участке цепи электрический ток не постоянный, то напряжение и сила тока постоянно изменяется, при этом у обычного переменного тока средние значения напряжения и силы тока равны нулю. Однако средняя мощность выделяемого при этом тепла нулю не равна. Поэтому применяют следующие понятия: · мгновенные напряжение и сила тока, то есть действующие в данный момент времени. · амплитудные напряжение и сила тока, то есть максимальные абсолютные значения · эффективные (действующие) напряжение и сила тока определяются тепловым действием тока, то есть имеют те же значения, которые они имеют у постоянного тока с таким же тепловым эффектом.[11] Плотность тока — вектор, абсолютная величина которого равна отношению силы тока, протекающего через некоторое сечение проводника, перпендикулярное направлению тока, к площади этого сечения, а направление вектора совпадает с направлением движения положительных зарядов, образующих ток. Согласно закону Ома в дифференциальной форме плотность тока в среде {\displaystyle {\vec {j}}}
Магнитное поле. Магнитное поле – это особая форма материи, которая создается магнитами, проводниками с током (движущимися заряженными частицами) и которую можно обнаружить по взаимодействию магнитов, проводников с током (движущихся заряженных частиц). Вектор магнитной индукции(В) - это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М. Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
Магнитная индукция - это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля. Единица магнитной индукции - тесла (Тл). Мы бы никогда не знали о магнитном поле, если бы оно себя не проявляло. Определить наличие поля можно стрелкой компаса. Стрелка компаса будет только сигнализатором наличия поля. Для получения количественных величин стрелка непригодна. В качестве измерителя поля можно использовать вращающуюся рамку.
Амплитуда напряжения на токосъемных кольцах равна
Где: N – число витков в рамке; Ф – магнитный поток Вб; ω – угловая частота вращения равная 2π f По замеренному напряжению можно рассчитать магнитный поток, измеряемый в веберах (Вб). Магнитный поток и есть величина, характеризующая поле. Зная магнитный поток, можно рассчитать напряжение, которое мы можем получить в генераторе. На практике чаще пользуются понятием плотности магнитного потока, т.е. потоком, проходящим сквозь площадку площадью 1 квадратный метр. Плотность магнитного потока называется магнитной индукцией. B = Ф/ S Магнитная индукция измеряется в теслах (Тл). Причиной возникновения магнитного потока является электрический ток. Магнитная индукция на расстоянии r от прямолинейного проводника равна:
По центру витка с током радиуса r магнитная индукция будет равна
Этой характеристикой магнитного потока – индукцией и можно было бы ограничиться при изучении магнетизма. Но традиционно преподается, что электрический ток порождает напряженность магнитного поля, а уж та в свою очередь порождает индукцию. Это напоминает индийский уклад офиса. В Индии начальник, чтобы включить вентилятор вызывает секретаршу. Та говорит: «Хорошо», - кланяется и уходит; через полчаса приходит электрик и, наконец, вентилятор начинает вращаться.. Напряженность магнитного поля измеряется в А/м. Для прямолинейного провода с током
Для витка с током напряженность в центре витка равна
Это те же самые формулы, которые приведены выше для индукции. Различаются они лишь магнитной постоянной μ0. Индукция в вакууме или воздухе равна
Где: μ0 - магнитная постоянная, равная 4π·10-7 То есть, индукция и напряженность различаются только масштабом единиц. И одно из этих понятий для наших сугубо практических целей излишне. И можно было бы все формулы и графики пересчитать на B, но читателям этой статьи придется пользоваться специальной литературой, где H наличествует, поэтому я оставлю по большинству традиционный стиль формул.
Сила Лоренца. Сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.
Где q – заряд частицы; V – скорость заряда; B – индукции магнитного поля; а – угол между вектором скорости заряда и вектором магнитной индукции.
Направление силы Лоренца определяется по правилу левой руки:
Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца
Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию). Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0, и заряд в магнитном поле движется равномерно и прямолинейно. Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной
и создает центростремительное ускорение равное
В этом случае частица движется по окружности.
Согласно второму закону Ньютона: сила Лоренца равна произведению массы частицы на центростремительное ускорение
тогда радиус окружности
а период обращения заряда в магнитном поле
Сила Ампера. Ампер изучал действие магнитного поля на проводники с током и установил, что сила
Направление силы Ампера находится по правилу векторного произведения – по правилу левой руки: четыре вытянутых пальца левой руки расположить по направлению тока, вектор Модуль силы Ампера
где α – угол между векторами Если поле однородно, а проводник с током конечных размеров, то
При
Электромагнитная индукция. Электромагнитная индукция (индукция значит наведение) это явление, при котором в замкнутом контуре возникает электрический ток при изменении магнитного потока, пронизывающего его. Закон электромагнитной индукции( ЭДС) индукция в контуре равна скорости изменения магнитного поля сквозь поверхность, ограниченную контуром.
Закон Фарадея. Электролизом -называют процессы, протекающие на электродах под действием электрического тока, подаваемого от внешнего источника тока через электролиты. Первый закон Фарадея: масса вещества m, выделяемая на электроде электрическим током, пропорциональная количеству электричества Q, прошедшему через электролит: m = kQ, но Q =It (1) где I – сила тока, А; t – время пропускание тока, с. m = kIt (2) k – коэффициент пропорциональности, равный количеству вещества, выделяемого при прохождении одного кулона (Кл) электричества (электрохимический эквивалент). Второй закон Фарадея: массы различных веществ, выделенных одним и тем же количеством электричества, пропорциональных их химическим эквивалентам (Мэ):
Для выделения 1 грамма эквивалента вещества требуется пропустить через электролит одно и тоже количество электричества, равное приблизительно 96500 Кл (число Фарадея). Следовательно:
Подставив последнее уравнение в (2), получим формулу, объединяющую оба закона Фарадея.
Соотношение (3) используют в расчетах процессов при электролизе. При практическом проведении электролиза всегда некоторая часть электрической энергии затрачивается на побочные процессы. Важной характеристикой рентабельности установки для проведения электролиза (электролизера) является выход по току (h, %): h = где mпр – масса фактически выделенного вещества; mтеор – масса вещества, которая должна была выделиться в соответствии с законом Фарадея. На процесс электролиза существенно влияет плотность тока, то есть сила тока, приходящаяся на единицу рабочей поверхности электрода.
Самоиндукция. Самоиндукция - явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока. Возникающая при этом ЭДС называется ЭДС самоиндукции. ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи. Если длина соленоида l гораздо больше его диаметра d (l>>d), то к нему можно применить формулы для бесконечно длинного соленоида. Тогда B=µµ0I N/l. Значит Индуктивность. Электрический ток, проходящий по контуру, создает вокруг него магнитное поле. Магнитный поток Ф через контур этого проводника (его называют собственным магнитным потоком) пропорционален модулю индукции В магнитного поля внутри контура, а индукция магнитного поля в свою очередь пропорциональна силе тока в контуре. Следовательно, собственный магнитный поток через контур прямо пропорционален силе тока в контуре:
Коэффициент пропорциональности L между силой тока I в контуре и магнитным потоком Ф, создаваемым этим током, называется индуктивностью контура. Индуктивность контура зависит от размеров и формы контура, от магнитных свойств среды, в которой находится контур. Так, индуктивность однослойного соленоида можно рассчитать по формуле
где Единицей индуктивности в СИ является генри (Гн). Эта единица определяется на основании формулы
Индуктивность контура равна 1 Гн, если при силе постоянного тока 1 А магнитный поток через контур равен 1 Вб: 1 Гн = (1 Вб)А. Энергия магнитного поля. Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения, магнитная составляющая электромагнитного поля. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Энергия магнитного поля, создаваемого током в замкнутом контуре индуктивностью L, равна Энергия магнитного поля катушки с индуктивностью L, создаваемого током I, равна
Линза и ее характеристики. Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), и фокусным расстоянием. Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, показатель преломления, коэффициент дисперсии, показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне. Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
Виды линз:
Использование линзы для изменения формы волнового фронта. Здесь плоский волновой фронт становится сферическим при прохождении через линзу Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски. Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равна нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна). Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.
Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре). Формула тонкой линзы. Обозначим через d расстояние от предмета до линзы и f от изображения до линзы. Отношение высоты изображения к высоте предмета, назовем увеличением линзы и обозначим через гамма. Тогда можно вывести такую формулу:
Предмет обозначим AB, изображение – A'B'. Рассмотрим две пары подобных треугольников AOB~A'O'B' (Рис. 10), и из этого можно вывести еще одну формулу:
Рис. 10. Геометрическая задача по нахождению изображения Также из подобия треугольников CFO и A'F'B' следует, что:
Теперь мы можем приравнять полученные равенства, производим несложные арифметические вычисления и получаем конечную формулу:
Интерференция света. Интерференция — взаимное усиление или ослабление двух или большего числа волн при их наложении друг на друга. В результате интерференции происходит перераспределение энергии светового излучения в пространстве. Устойчивая (стационарная, постоянная во времени) интерференционная картина наблюдается при сложении когерентных волн. Требование когерентности волн — ключевое при рассмотрении интерференции. Разберем его на примере сложения двух волн одинаковой частоты. Пусть в некоторой точке пространства они возбуждают одинаково направленные (E̅1 ↑↑ E̅2) колебания: E̅1 sin (ω̅t + φ1) и E̅2 sin (ω̅t + φ2). Тогда величина амплитуды результирующего колебания E̅ sin (ω̅t + φ) равна E = √(E12 + E22 + 2E1E2 cos δ), где δ = φ1 — φ2. Если разность фаз δ постоянна во времени, то волны называются когерентными. Для некогерентных волн δ случайным образом изменяется во времени, поэтому среднее значение cos δ равно нулю. Поскольку интенсивность волны пропорциональна квадрату амплитуды, то в случае сложения некогерентных волн интенсивность результирующей волны I просто равна сумме интенсивностей каждой из волн: I = I1 + I2. При сложении же когерентных волн интенсивность результирующего колебания I = I1 + I2 + 2√(I1I2 cos δ), в зависимости от значения cos δ, может принимать значения и большие, и меньшие, чем I1 + I2. Так как значение δ в общем случае зависит от точки наблюдения, то и интенсивность результирующей волны будет различной в разных точках. Именно это имелось в виду, когда выше говорилось о перераспределении энергии в пространстве при интерференции волн. Метод Юнга Источником света служит ярко освещенная щель S, от которой свет падает на две равноудаленные щели s1, и s2, параллельные щели S (рис. 4.5).
Рис. 4.5. Метод Юнга наблюдения интерференции Таким образом, щели S1 и S2 являются источниками когерентных пучков света. Когерентность, естественно, имеет место при условии, что <
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.195.90 (0.01 с.) |

 , действующей на помещенный в данную точку поля заряд, к этому заряду
, действующей на помещенный в данную точку поля заряд, к этому заряду  для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:
для каждой точки поля не зависит от заряда и может рассматриваться как силовая характеристика поля — напряженность электрического поля:  .
. .
. Линии напряженности электрического поля (силовые линии) – это непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с векторами напряженности. Эти линии называют силовыми линиями электрического поля, или линиями напряженности.
Линии напряженности электрического поля (силовые линии) – это непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с векторами напряженности. Эти линии называют силовыми линиями электрического поля, или линиями напряженности.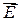 измеряется в ньютонах на кулон (Н/Кл).
измеряется в ньютонах на кулон (Н/Кл). .Величина напряженности поля точечного заряда
.Величина напряженности поля точечного заряда  на расстоянии
на расстоянии  от него равна
от него равна  , или в скалярной форме
, или в скалярной форме  . Вектор напряженности точечного заряда в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд.
. Вектор напряженности точечного заряда в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд. В случае точечного заряда линии напряженности – радиальные прямые, выходящие из заряда, если он положителен, и входящие в него, если заряд отрицателен.
В случае точечного заряда линии напряженности – радиальные прямые, выходящие из заряда, если он положителен, и входящие в него, если заряд отрицателен. , то результирующая напряженность поля в этой точке равна
, то результирующая напряженность поля в этой точке равна  .
.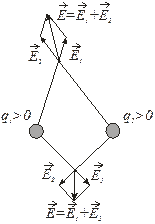 Допустим поле создается двумя точечными неподвижными положительными зарядами
Допустим поле создается двумя точечными неподвижными положительными зарядами  и
и 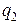 (
(
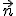 (рис. 157).
(рис. 157).
 . (1)
. (1) — скалярное произведение векторов
— скалярное произведение векторов  и;En— нормальная к площадке компонента вектора напряженности.
и;En— нормальная к площадке компонента вектора напряженности.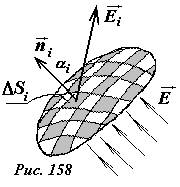

 где
где —поток вектора напряжённости электрического поля через замкнутую поверхность
—поток вектора напряжённости электрического поля через замкнутую поверхность  .
. —полный заряд, содержащийся в объёме, который ограничивает поверхность.
—полный заряд, содержащийся в объёме, который ограничивает поверхность. — электрическая постоянная.
— электрическая постоянная.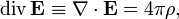

 — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а
— объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а  — оператор набла.
— оператор набла. через поперечное сечение проводника, к величине этого промежутка времени.
через поперечное сечение проводника, к величине этого промежутка времени. где Мо - магнитная постоянная, R - расстояние, I - сила тока в проводнике.
где Мо - магнитная постоянная, R - расстояние, I - сила тока в проводнике.














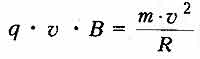
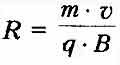

 , с которой магнитное поле действует на элемент проводника
, с которой магнитное поле действует на элемент проводника  с током, находящимся в магнитном поле
с током, находящимся в магнитном поле  , прямо пропорциональна силе тока и векторному произведению элемента проводника
, прямо пропорциональна силе тока и векторному произведению элемента проводника  – Сила Ампера (или закон Ампера)
– Сила Ампера (или закон Ампера) с помощью правой руки: вращаем четыре пальца правой руки от первого сомножителя
с помощью правой руки: вращаем четыре пальца правой руки от первого сомножителя 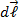 ко второму
ко второму  ,
, .
. ,
, .
.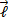
 .
.
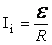 . e не зависит от свойств контура:
. e не зависит от свойств контура:  . ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.
. ЭДС индукции в замкнутом контуре прямо пропорциональна скорости изменения магнитного потока через площадь, ограниченную этим контуром.


 (3)
(3) (4)
(4) -ЭДС самоиндукции
-ЭДС самоиндукции V.
V.

 — магнитная проницаемость сердечника,
— магнитная проницаемость сердечника, 
 где I — сила тока в контуре.
где I — сила тока в контуре.