
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы расчета по предельным состояниям.Содержание книги
Поиск на нашем сайте
Лекция №2 Основы расчета по предельным состояниям. Расчет элементов конструкций цельного сечения Элементами деревянных конструкций называют доски, бруски, брусья и бревна цельного сечения с размерами, указанными в сортаментах пилёных и круглых материалов. Они могут являться самостоятельными конструкциями, например, балками или стойками, а также стержнями более сложных конструкций. Усилия в элементах определяют общими методами строительной механики. Проверка прочности и прогибов элемента заключается в определении напряжений в сечениях, которые не должны превышать расчетных сопротивлений древесины, а также его прогибов, которые не должны превосходить предельных, установленных нормами проектирования. Деревянные элементы рассчитывают в соответствии со СНиП II-25-80.
Растянутые элементы
Древесина на растяжение работает почти упруго и показывает высокую прочность. Разрушение происходит хрупко в виде почти мгновенного разрыва. Стандартные образцы при испытаниях на растяжение имеют вид «восьмерки». Как видно из диаграммы растяжения древесины без пороков, зависимость деформаций от напряжений близка к линейной, а прочность достигает 100 МПа. Однако прочность реальной древесины при растяжении, учитывая ее значительные колебания, большое влияние пороков и длительности нагружения значительно ниже: для неклееной древесины I сорта Rр =10 МПа, для клееной древесины влияние пороков уменьшается, поэтому Rр =12 МПа. Прочность растянутых элементов в тех местах, где есть ослабления снижается в результате концентрации напряжений у их краев, т.е. вводится коэффициент условия работы m0 =0,8. Тогда получается расчетное сопротивление Rр =8 МПа. Проверочный расчет растянутых элементов производится по формуле: σ
Сжатые элементы
Стандартные образцы при испытании на сжатие имеют вид прямоугольной призмы с размерами, указанными на рис. 2. Древесина работает на сжатие надежно, но не вполне упруго. Примерно до половины предела прочности рост деформаций происходит по закону близкому к линейному, и древесина работает почти упруго. При росте нагрузки увеличение деформаций все более опережает рост напряжений, указывая на упруго-пластический характер работы древесины. Разрушение образцов без пороков происходит при напряжениях, достигающих 44 МПа, пластично, в результате потери устойчивости ряда волокон, о чем свидетельствует характерная складка. Пороки меньше снижают прочность древесины, чем при растяжении, поэтому расчетное сопротивление реальной древесины при сжатии выше и составляет для древесины 1 сорта Rс= 14÷16 МПа, а для 2 и 3 сортов эта величина немного ниже. Расчет на прочность сжатых элементов производится по формуле: σ Rс – расчетное сопротивление сжатию. Аналогичным образом рассчитываются и сминаемые по всей поверхности элементы. Сжатые стержни, имеющие большую длину и не закрепленные в поперечном направлении должны быть, помимо расчета на прочность, рассчитаны на продольный изгиб. Явление продольного изгиба заключается в том, что гибкий центрально-сжатый прямой стержень теряет свою прямолинейную форму (теряет устойчивость) и начинает выпучиваться при напряжениях, значительно меньших предела прочности. Проверку сжатого элемента с учетом его устойчивости производят по формуле: σ
φ – коэффициент продольного изгиба.
1. При отсутствии ослаблений 2. При ослаблениях, не выходящих на кромки, если площадь ослаблений не превышает 25% 3. То же, если площадь ослаблений превышает 20% 1. При симметричных ослаблениях, выходящих на кромки
При несимметричном ослаблении, выходящем на кромки, элементы рассчитывают как внецентренно сжатые. Коэффициент продольного изгиба φ всегда меньше 1, учитывает влияние устойчивости на снижение несущей способности сжатого элемента в зависимости от его расчетной максимальной гибкости λ. Гибкость элемента равна отношению расчетной длины l0 к радиусу инерции сечения элемента:
Расчетную длину элемента l0 следует определять умножением его свободной длины l на коэффициент μ0: l0=l μ0, где коэффициент μ0 принимается в зависимости от типа закрепления концов элемента: - при шарнирно закрепленных концах μ0 =1; - при одном шарнирно закрепленном, а другом защемленном μ0 =0,8; - при одном защемленном, а другом свободном нагруженном конце μ0 =2,2; - при обоих защемленных концах μ0 =0,65. Гибкость сжатых элементов ограничивается с тем, чтобы они не получились недопустимо гибкими и недостаточно надежными. Отдельные элементы конструкций (отдельные стойки, пояса, опорные раскосы ферм и т.п.) должны иметь гибкость не более 120. Прочие сжатые элементы основных конструкций – не более 150, элементы связей – 200. При гибкости более 70 (λ >70) сжатый элемент теряет устойчивость, когда напряжения сжатия в древесине еще невелики и она работает упруго. Коэффициент продольного изгиба (или коэффициент устойчивости), равный отношению напряжения в момент потери устойчивости σкр к пределу прочности при сжатии Rпр, определяют по формуле Эйлера с учетом постоянного отношения модуля упругости древесины к пределу прочности:
А =3000 – для древесины, А =2500 – для фанеры. При гибкостях, равных и меньших 70 (λ ≤70) элемент теряет устойчивость, когда напряжения сжатия достигают упругопластической стадии и модуль упругости древесины понижается. Коэффициент продольного изгиба при этом определяют с учетом переменного модуля упругости по упрощенной теоретической формуле:
При подборе сечения используют формулу расчета на устойчивость, предварительно задаваясь величиной λ и φ.
Изгибаемые элементы
В изгибаемых элементах от нагрузок, действующих поперек продольной оси, возникают изгибающие моменты М и поперечные силы Q, определяемые методами строительной механики. Например, в однопролетной балке пролетом l от равномерно-распределенной нагрузки q возникают изгибающие моменты От изгибающего момента в сечениях элемента возникают деформации и напряжения изгиба σ, которые состоят из сжатия в одной части сечения и растяжения в другой, в результате элемент изгибается. Диаграмма как и для сжатия, примерно до половины, имеет линейное очертание, затем изгибается, показывая ускоренный рост прогибов.
Косой изгиб Возникает в элементах, оси сечений которых расположены наклонно к направлению нагрузок, как например, в брусчатых прогонах скатных покрытий.
qx=qsinα; qy=qcosα; Mx=Msinα; My=Mcosα. Вертикальная нагрузка q и изгибающие моменты М при косом изгибе под углом α раскладываются на нормальную (qy) и скатную (qx) составляющие.
σ= Подбор сечений косоизгибаемых элементов производят методом попыток. Расчет по прогибам производят с учетом геометрической суммы прогибов относительно каждой из осей сечения:
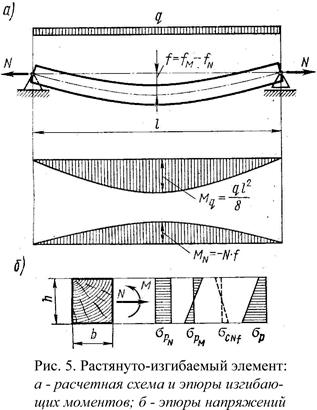
Сжато-изгибаемые элементы
Работают одновременно на сжатие и изгиб. Так работают, например, верхние сжатые пояса ферм, нагруженные дополнительно межузловой поперечной нагрузкой, а также при эксцентричном приложении сжимающей силы (внецентренно-сжатые элементы). В сечениях сжато-изгибаемого элемента возникают равномерные напряжения сжатия от продольных сил N и напряжения сжатия и растяжения от изгибающего момента М, которые суммируются. Искривление сжато-изгибаемого элемента поперечной нагрузкой приводит к появлению дополнительного изгибающего момента с с максимальным значением: МN=N·f, где f – прогиб элемента. Расчет на прочность сжато-изгибаемых элементов выполняют по формуле:
Мд – изгибающий момент по деформированной схеме от действия поперечных и продольных нагрузок. Для шарнирно-опертых элементов при симметричных эпюрах изгибающих моментов синусоидального, параболического и близких к ним очертаний:
М – изгибающий момент в расчетном сечении без учета дополнительного момента от продольной силы; ξ – коэффициент, изменяющийся от 1 до 0, учитывающий дополнительный момент от продольной силы вследствие прогиба элемента, определяемый по формуле:
φ – коэффициент продольного изгиба (коэффициент устойчивости) для сжатых элементов. Кроме проверки на прочность, сжато-изогнутые элементы проверяются на устойчивость по формуле:
Fбр – площадь брутто с максимальными размерами сечения элемента на участке lp; Wбр – максимальный момент сопротивления на рассматриваемом участке lp; n =2 – для элементов без закрепления растянутой зоны из плоскости деформирования, n =1 – для элементов, имеющих закрепления в растянутой зоне из плоскости деформирования;
φ – коэффициент устойчивости для сжатия, определяемый по формуле:
А =3000 – для древесины, А =2500 – для фанеры; φм – коэффициент устойчивости для изгиба, формула для определения этого коэффициента была дана раньше.
Лекция №2 Основы расчета по предельным состояниям.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 369; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.50.186 (0.009 с.) |

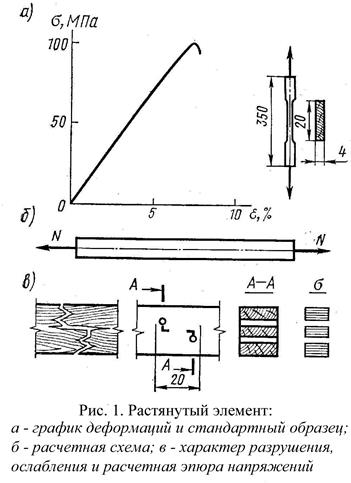 На растяжение работают нижние пояса и отдельные раскосы ферм, затяжки арок и других сквозных конструкций. Растягивающее усилие N действует вдоль оси элемента и во всех точках его поперечного сечения возникают растягивающие напряжения σ, которые с достаточной точностью считаются одинаковыми по величине.
На растяжение работают нижние пояса и отдельные раскосы ферм, затяжки арок и других сквозных конструкций. Растягивающее усилие N действует вдоль оси элемента и во всех точках его поперечного сечения возникают растягивающие напряжения σ, которые с достаточной точностью считаются одинаковыми по величине. , где
, где – площадь рассматриваемого поперечного сечения, причем ослабления, расположенные на участке длиной 20 см. считаются совмещенными в одном сечении. Для подбора сечений пользуются этой же формулой, но относительно искомой (требуемой) площади
– площадь рассматриваемого поперечного сечения, причем ослабления, расположенные на участке длиной 20 см. считаются совмещенными в одном сечении. Для подбора сечений пользуются этой же формулой, но относительно искомой (требуемой) площади  .
.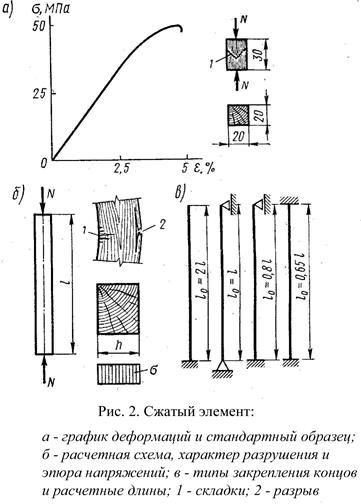 На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм. В сечениях элемента от сжимающего усилия N, действующего вдоль его оси, возникают почти одинаковые по величине сжимающие напряжения σ (эпюра прямоуголная).
На сжатие работают стойки, подкосы, верхние пояса и отдельные стержни ферм. В сечениях элемента от сжимающего усилия N, действующего вдоль его оси, возникают почти одинаковые по величине сжимающие напряжения σ (эпюра прямоуголная). , где
, где , где
, где – расчетная площадь поперечного сечения,
– расчетная площадь поперечного сечения,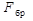 ,
,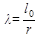 ;
; 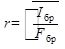 .
.
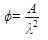 , где
, где , где
, где =0,8 – коэффициент для древесины;
=0,8 – коэффициент для древесины;
 и поперечные силы
и поперечные силы  .
.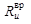 =80 МПа – предел прочности чистой древесины на изгиб при кратковременных испытаниях. Разрушение образца начинается с появления складок в крайних сжатых волокнах и завершается разрывом крайних растянутых. Расчетное сопротивление изгибу по СНиП II-25-80 рекомендуется принимать таким же, как и при сжатии, т.е. для 1 сорта Rи =14 МПа – для элементов прямоугольного сечения высотой до 50 см. Брусья с размерами сечения 11 – 13 см. при высоте сечения 11 – 50 см. имеют меньше перерезанных волокон при распиловке, чем доски, поэтому их прочность повышается до Rи =15 МПа. Бревна шириной свыше13 см. при высоте сечения 13 – 50 см. совсем не имеют перерезанных волокон, поэтому Rи =16 МПа.
=80 МПа – предел прочности чистой древесины на изгиб при кратковременных испытаниях. Разрушение образца начинается с появления складок в крайних сжатых волокнах и завершается разрывом крайних растянутых. Расчетное сопротивление изгибу по СНиП II-25-80 рекомендуется принимать таким же, как и при сжатии, т.е. для 1 сорта Rи =14 МПа – для элементов прямоугольного сечения высотой до 50 см. Брусья с размерами сечения 11 – 13 см. при высоте сечения 11 – 50 см. имеют меньше перерезанных волокон при распиловке, чем доски, поэтому их прочность повышается до Rи =15 МПа. Бревна шириной свыше13 см. при высоте сечения 13 – 50 см. совсем не имеют перерезанных волокон, поэтому Rи =16 МПа.
 Проверку прочности при косом изгибе производят по формуле:
Проверку прочности при косом изгибе производят по формуле: .
. .
.
 , где
, где , где
, где , где
, где , где
, где


