
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задачи коммивояжера методом ветвей и границ.Содержание книги
Поиск на нашем сайте
Цель работы: получить навыков в решении задачи коммивояжера методом ветвей и границ.. 1.Краткие теоретические сведения. Основным методом решения задачи коммивояжера является метод ветвей и границ (МВиГ). Этот метод является универсальным и может применяться для решения практически всех дискретных экстремальных задач. Основные принципы МВиГ для решения задачи минимизации состоят в следующем. 1) Ветвление. Исходная задача разбивается (ветвится) на две или более подзадачи таким образом, что решение исходной задачи является решением хотя бы одной из подзадач. Каждая из подзадач, в свою очередь, аналогичным образом ветвится на более мелкие подзадачи. Процесс может повторяться до тех пор, пока получаемая подзадача не становится тривиальной и ее решение может быть легко найдено. Указанный процесс можно представить в виде так называемого дерева ветвлений. Вершины дерева ветвлений соответствуют подзадачам и разбиты на уровни. Исходная задача является вершиной нулевого уровня. Подзадачи, полученные из исходной задачи, являются вершинами первого уровня. Подзадачи, полученные из вершин первого уровня, являются вершинами второго уровня, и т.д. Дуги направлены из вершин уровня 2) Построение нижних и верхних оценок минимального значения целевой функции. Для исходной задачи, а также для любой ее подзадачи могут быть найдены числа
где Нижняя оценка может быть получена в результате решения релаксированной или ослабленной задачи, например, задачи коммивояжера, в которой стоимости всех дуг, входящих в данную вершину, заменены на минимальную из них, и аналогично изменены (уменьшены) стоимости всех дуг, выходящих из данной вершины. Верхняя оценка может быть получена в результате отыскания любого допустимого решения рассматриваемой задачи и вычисления соответствующего значения целевой функции. Для задачи коммивояжера достаточно подсчитать суммарную стоимость дуг для какого-нибудь допустимого маршрута (допустимой перестановки). Наилучшая, т.е.наименьшая из всех имеющихся в наличии верхних оценок, называется (текущим) рекордом.
Может оказаться, что задача отыскания нижней и/или верхней оценки сама является сложной. В этом случае соответствующая оценка не используется и можно положить 3) Отсеивание вариантов. В случае если для некоторой подзадачи ее нижняя оценка превосходит либо равна рекорду, такую подзадачу можно далее не ветвить, так как ее решение будет заведомо хуже либо не лучше решения, соответствующего рекорду. 4) Оптимальное решение. Процесс вычислений прекращается, когда нет ни одной подзадачи, которая может продолжать ветвиться. В этом случае оптимальное решение соответствует текущему рекорду. В приведенном методе остается неопределенным способ выбора подзадачи для ветвления. Такие способы могут быть различными. Наиболее употребимым является способ, при котором ветвят ту подзадачу, которой соответствует наименьшее значение нижней оценки либо ту, которая быстрее приведет к тривиальной подзадаче. Различают методы ветвления в глубину и в ширину. При ветвлении в глубину всегда ветвят одну из подзадач наибольшего уровня. Такое ветвление быстрее приведет к построению полного допустимого решения. При ветвлении в ширину ветвят подзадачи одного уровня до тех пор, пока все такие подзадачи не будут рассмотрены. Такое ветвление позволяет получать больше нижних и верхних оценок и может привести к большему количеству отсеянных вариантов. Однако требуется больше памяти для хранения промежуточных результатов по сравнению с ветвлением в глубину. Рассмотрим задачу проведения рекламной кампании в четырех областных центрах Украины Пусть матрица (таблица) стоимостей переезда между городами выглядит следующим образом:
Будем решать задачу методом ветвления вглубь. Вначале построим "приведенную задачу", эквивалентную исходной. Используем процедуру "приведение таблицы", состоящую в вычитании наименьшего числа в каждом столбце (строке), затем наименьшего числа в каждой строке (столбце) и суммировании этих чисел (из каждого города нужно выехать и в каждый город нужно въехать). Получаем
Приведенная таблица:
Для элементов приведенной таблицы оставим обозначения Очевидно, что нижняя оценка для приведенной задачи равна Далее разветвим исходную задачу. Ветвление будем осуществлять по вхождению или невхождению некоторой дуги в маршрут. Обычно выбирают дугу 1) максимальной, но не равной В подзадаче Выбираем дугу (1,2) для дальнейших ветвлений. Нарисуем начальное дерево ветвлений, состоящее из 3 вершин ‑ начальной 0 и вершин, обозначенных
Припишем вершинам соответствующие значения Рассмотрим подзадачу
Используем процедуру "приведение таблицы", состоящую в вычитании наименьшего числа в каждом столбце (строке), затем наименьшего числа в каждой строке (столбце) и суммировании этих чисел (из каждого города нужно выехать и в каждый город нужно въехать). Получаем
Вычисляем В матрице стоимости подзадачи Вычисляем соответствующие им значения
В соответствии с принятым правилом ветвления, для ветвления выбираем дугу, дающую наибольшее значение нижней оценки при ее невхождении в маршрут. В рассматриваемом случае – это дуга
Рассмотрим подзадачу
Процесс ветвления останавливается для матриц По дереву ветвлений восстанавливаем построенные частичные маршруты:
Получили новый рекорд Так как нет ни одной подзадачи, которая может продолжать ветвиться, процесс вычислений прекращается и оптимальное решение соответствует текущему значению рекорда. Таким образом решением задачи коммивояжера полный маршрут
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 174; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.254.121 (0.011 с.) |

 в вершины уровня
в вершины уровня  . В каждую вершину входит ровно одна дуга.
. В каждую вершину входит ровно одна дуга. и
и  такие, что
такие, что ,
, ‑минимальное значение целевой функции в задаче или подзадаче,
‑минимальное значение целевой функции в задаче или подзадаче,  ,
,  .
.

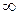
 . Далее можно работать с приведенной матрицей. Для получения реальной стоимости любого маршрута необходимо добавить к получаемой из приведенной таблицы стоимости величину
. Далее можно работать с приведенной матрицей. Для получения реальной стоимости любого маршрута необходимо добавить к получаемой из приведенной таблицы стоимости величину  .
. .
. . Для отыскания верхней оценки построим какой-нибудь маршрут коммивояжера. Например, разумным будет включить в этот маршрут дугу минимальной стоимости, скажем,
. Для отыскания верхней оценки построим какой-нибудь маршрут коммивояжера. Например, разумным будет включить в этот маршрут дугу минимальной стоимости, скажем,  . Далее выбрать дугу минимальной стоимости вида
. Далее выбрать дугу минимальной стоимости вида  . Это -
. Это -  . Далее, выбрать дугу минимальной стоимости вида
. Далее, выбрать дугу минимальной стоимости вида  . Это
. Это  . Получаем верхнюю оценку
. Получаем верхнюю оценку  . Она является рекордом
. Она является рекордом 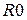 . Отметим, что маршруту коммивояжера соответствует такое множество элементов таблицы, что в каждой строке и каждом столбце находится ровно один элемент этого множества. Однако, не каждое множество, содержащее ровно один элемент в каждой строке и каждом столбце является маршрутом коммивояжера. Такому множеству может соответствовать более одного цикла в графе.
. Отметим, что маршруту коммивояжера соответствует такое множество элементов таблицы, что в каждой строке и каждом столбце находится ровно один элемент этого множества. Однако, не каждое множество, содержащее ровно один элемент в каждой строке и каждом столбце является маршрутом коммивояжера. Такому множеству может соответствовать более одного цикла в графе.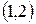 ,
,  ,
,  .
. дуга
дуга  1 должна выйти и какая-то дуга должна войти в 2. Можно добавить к нижней оценке сумму наименьших чисел в указанных строке и столбце
1 должна выйти и какая-то дуга должна войти в 2. Можно добавить к нижней оценке сумму наименьших чисел в указанных строке и столбце  и вычислить
и вычислить  . Аналогично вычисляем
. Аналогично вычисляем  ,
,  ,
,  ,
,  ,
,  .. Наибольшее значение равно
.. Наибольшее значение равно  .
. (соответствующая дуга не входит в маршрут коммивояжера) и
(соответствующая дуга не входит в маршрут коммивояжера) и 
 .
. . Поскольку дуга
. Поскольку дуга  ). Перепишем матрицу стоимостей для подзадачи
). Перепишем матрицу стоимостей для подзадачи 

 и приведенную таблицу стоимостей для подзадачи
и приведенную таблицу стоимостей для подзадачи  .
. ,
,  ,
,  ,
,  ,
, 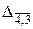 . Для этого полагаем стоимость удаляемой дуги равной
. Для этого полагаем стоимость удаляемой дуги равной  ,
,  ,
,  ,
,  .
. . Ее и выбираем для ветвления подзадачи
. Ее и выбираем для ветвления подзадачи 
 . Поскольку дуга
. Поскольку дуга 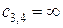 ). Перепишем матрицу стоимостей для подзадачи
). Перепишем матрицу стоимостей для подзадачи  . В этом случае можно найти решение либо определить, что оно не существует.
. В этом случае можно найти решение либо определить, что оно не существует.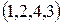 стоимости
стоимости .
.
 . Из условия отсеивания ветки
. Из условия отсеивания ветки  и
и  можно отсечь.
можно отсечь.



