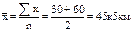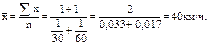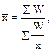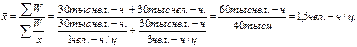Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средняя гармоническая величина.Содержание книги
Поиск на нашем сайте
Название средней гармонической величины неслучайно, так эта средняя "гармонирует" со средней арифметической величиной. Для ранжированного ряда используется средняя гармоническая простая величина, которую можно записать следующим образом.
где n – общая численность вариант; Допустим, имеются данные о том, что при перевозке картофеля скорость движения автомобиля с грузом составляет 30 км/ч, без груза – 60 км/ч. необходимо найти среднюю скорость движения автомобиля. На первый взгляд представляется совсем несложное решение задачи: применить способ средней арифметической простой величины, т.е. Однако, если иметь в виду, что скорость движения равна пройденному пути, разделённому на затраченное время, то совершенно очевидно, что полученный результат (45 км/ч) оказывается неточным, так как на прохождение одного и того же автомобиля с грузом и без груза (туда и обратно) затраты времени будут существенно различаться. Следовательно, более точная средняя скорость движения автомобиля с грузом и без груза может быть рассчитана по средней гармонической простой величине:
Таким образом, средняя скорость движения автомобиля с грузом и без груза составляет не 45, а 40 км/ч. В дискретный или интервальных рядах используются средняя гармоническая взвешенная величина:
где W – произведение варианты на частоту (взвешенная варианта, xf). Рассмотрим пример. Трудоемкость производства картофеля в первом подразделении сельскохозяйственного предприятия составляет 1 чел.-ч., во втором – 3 чел.-ч. В обоих подразделения на производство картофеля затрачено по 30 тыс. чел.-ч. необходимо рассчитать среднюю арифметическую трудоёмкость картофеля в сельскохозяйственном предприятии. Само собой разумеется, что беглый взгляд на исходную информацию подсказывает простое решение: среднюю трудоёмкость легко найти как полу сумму трудоёмкости картофеля в двух подразделениях, т. е. по способу средней арифметической простой величины:
Однако, при таком решении совершается две ошибки. Первая, принципиальная ошибка заключается в том, что при расчёте средней трудоемкости по способу средней арифметической простой величины не учитывается сущность самой трудоемкости, которая находится как отношение прямых затрат труда к объему продукции. Вторая ошибка состоит в том, что при решении не учтен приведенный по условию задачи конкретный объем затрат труда на производство картофеля (по 30 тыс. чел.-ч. в обоих подразделениях). Это позволяет рассчитать частоту (веса) для трудоемкости картофеля и, таким образом, найти среднюю арифметическую взвешенную трудоемкость, что будет успешно заменено путем применения средней гармонической взвешенной величины:
Таким образом, средняя трудоёмкость картофеля в сельхозпредприятии составляет не 2, как это было рассчитано выше, а 1,5 чел.-ч/ц. Средняя гармоническая величина применяется главным образом в тех случаях, когда варианты ряда представлены обратными значениями, а частоты (веса) скрыты в общем объеме изучаемого признака.
|
|||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.137.191 (0.01 с.) |

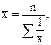
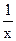 - обратное значение варианты.
- обратное значение варианты.