Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел 4. Методы синтеза и анализа криптографических алгоритмов с секретным ключом. ⇐ ПредыдущаяСтр 4 из 4
4.1 Принципы построения блочных шифров. Алфавитом блочного шифра является множество двоичных векторов-блоков открытого текста одинаковой длины (64, 128, 256, и т.д.). К.Шеннон сформулировал общие принципы шифрующих преобразований – перемешивание и рассеивание. Принцип перемешивания означает, что применение шифрпреобразования к наборам аргументов, отличающихся в незначительном числе позиций, должно приводить к существенному изменению результата. Обеспечить выполнение этого требования в общевм случае затруднительно. Шеннон предложил выполнять такое преобразование в виде суперпозиции нескольких простых некоммутирующих отображений. Блочные шифры реализуются путём применения к блокам открытого текста некоторых базовых преобразований. Используются базовые преобразования двух типов. «Перемешивающие» преобразования – сложные локальные преобразования над отделными частями шифруемых блоков. «Рассеивающие» преобразования – перестановки между собой частей шифруемых блоков. При этом перемешивание усложняет восстановление взаимосвязи статистических и аналитических свойств открытого и шифрованного текстов, а рассеивание уменьшает статистические особенности открытого текста и их влияние на шифртекст. Алгоритм преобразования выполняет некоторое число циклов (итераций). Каждый цикл выполняет несколько преобразований первого и второго типов. Это позволяет реализовывать циклы с применением однотипных узлов и выполнять расшифрование обработкой даннаых в обратной последовательности. Удобным механизмом для реализации базовых преобразований являются регистры сдвига. При этом рассеивающие преобразования определяются функциями обратной связи, а перемешивающие – сдвигами информации в регистре. Нашли применеие алгоритмы, в которых преобразования выполняются над векторами левой и правой половины регистра сдвига. Они могут быть реализованы сетью Фейстеля (см. рис. 2.3 – 2.4). Преобразовани сетью Фейстеля в i-м цикле шифрования имеет вид:
где Х1 , Х2 – две половины входного блока Х, Y1, Y2 - результат шифрования блока X на ключе k l с помощю функции f l . Алгоритм реализуется несколькими итерациями сети с использованием ключа k. Очередная итерация использует в качестве входного блока результат предыдущей итерации и ключ k l вычисляемый по ключу k. Ценность преобреобразование сетью заключается в том, что если f l не является обратимой функцией, преобразование сети Фейстеля обратимо.
Блочные алгоритмы сипользуются в следующих четырёх режимах: -режим электронной содовой книги (ЕCB); -режим сцепления блоков (СВС); -режим обратной связи по шифртексту (CFB); -режим обратной связи по выходу (OFB). Режимыимеют достоинства и недостатки. Достоинство ЕСВ – простота реализации. Недостаток – возможность проведения криптоанализа «со словарём». В случае повторения в открытом тексте одинаковых блоков, в шифртексте также появляются одинаковые блоки. При наличии большого числа пар открытого и шифровынного текста аналитик с большой вероятностью может восстанавливать другие блоки открытого текста по шифртексту. В режимах ЕCB и OFB искажение при передаче одного блока шифртекста приводит к искажению после расшифрования одного соответствующего блока открытого текста, но не влияет на следующие блоки. Это свойство используется для шифрования информации при передаче по каналам с большим числом искажений. Принципы построения алгоритмов поточного шифрования. Поточный шифр (ПШ) выполняет побуквенное зашифрование с помощью некоторого множества подстановочных преобразований алфавита открытых сообщений и является шифром замены с множествами шифрвеличин и шифробозначений, принадлежащих алфавиту открытых сообщений. Для построения многоалфавитного поточного шифра замены необходимо указать его распределеитель, устанавливающий порядок использования шифрующих преобразований, и сами эти преобразования (простые замены). Пусть: А – алфавит открытых сообщений;
x = a1,a2,…al – произвольный открытый текст; k
Тогда правило зашифрования:
Задача построения шифра сводится к выбору множества шифрующих преобразований Поточная шифрсистема представляет собой два основных блока. Первый блок вырабатывает последовательность номеров шифрующих преобразований и, фактически, управляет порядком процедуры. Этот блок называется управляющим блоком, а последовательность номеров – управляющей последовательностью (управляющей гаммой). Второй блок в соответствии с текущим номером управляющей последовательности реализует алгоритм зашифрования текущего знака. Он называется шифрующим блоком.
Управляющая гамма представляет собой псевдослучайную последовательность, соответствующую некоторой рекуррентной зависимости:
где Для получения рекуррентных последовательностей используются различные датчики псевдослучайных чисел. Требования к управляющему блоку: -период управляющей гаммы должен превышать максимально возможную длину открытых сообщений, подлежащих шифрованию; -статистические свойства гаммы должны приближаться к свойствам случайной равновероятной последовательности; -в гамме не должно быть простых аналитических зависимостей между близко расположенными знаками; -криптографический алгоритм получения знаков гаммы должен обеспечивать высокую сложность получения секретного ключа. Требования к шифрующему блоку: -применения алгоритма шифрования должно быть универсальным т.е. не зависеть от вида шифруемой информации; -шифрующий блок должен обеспечивать стойкость шифра при повторном использовании ключей. Типовые генераторы псевдослучайных последовательностей. Конгруэнтный генератор – формирует последовательность чисел на основе линейного конгруэнтного метода. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:
где a и c — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа Последовательность чисел, порождаемая линейным конгруэнтным методом, периодична с периодом, не превышающим m. При этом длина периода в точности равна m тогда и только тогда, когда: НОД(c,m) = 1 (то есть, c и m взаимно просты); a-1 кратно p для всех простых делителей p числа m; a-1 кратно 4, если m кратно 4. Статистические свойства получаемой последовательности случайных чисел полностью определяются выбором коэффициентов a и c. Для этих констант выписаны условия, гарантирующие удовлетворительное качество получаемых случайных чисел. При реализации выгодно выбирать где e —число битов в машинном слове, поскольку это позволяет избавиться от относительно медленной операции приведения по модулю. Младшие двоичные разряды сгенерированных таким образом случайных чисел демонстрируют поведение, далёкое от случайного, поэтому рекомендуется использовать только старшие разряды. В таблице ниже приведены наиболее часто используемые параметры линейных конгруэнтных генераторов, в частности, в стандартных библиотеках различных компиляторов (функция rand()). Особенностью линейного конгруэнтного метода является то, что если сомножитель и модуль соответствующим образом подобраны, то результирующая последовательность чисел будет статистически неотличима от случайной последовательности элементов множества { 0, 1, 2, …, m -1 }. Однако, все элементы этой последовательности однозначно определяются четырьмя параметрами: X 0, a, c, m.
Если криптоаналитик знает об использовании линейного конгруэнтного метода с известными параметрами, то известной становится вся последовательность чисел. В то же время, даже если криптоаналитик знает только лишь об использовании линейного конгруэнтного метода, то информация о небольшой части последовательности достаточна для выявления параметров метода и всех последующих элементов последовательности. В частности, если криптоаналитику известны значения
из которой можно получить значения параметров а, с и m. Поэтому, хотя линейный конгруэнтный метод порождает статистически хорошую псевдослучайную последовательность чисел, он не является криптографически стойким. У генератора Фибоначчи алгоритм похож на алгоритм генерации чисел Фибоначчи (Чи́сла Фибона́ччи — элементы числовой последовательности в которой каждое последующее число равно сумме двух предыдущих чисел). Генераторы этого типа используют некоторый начальный набор целых чисел – стартовое слово:
и два лага r и s причём r > s. Алгоритм генерации:
где символ В случае (+, -,) { Применяются также генераторы, основанные на задачах теории чисел, например, использующие рекурренту в конечном поле. Коэффициенты рекурренты выбираются так чтобы образующий полином являлся примитивным многочленом по модулю N.
4.4 Генераторы на основе линейных регистров сдвига. Последовательностью над полем P называют любую функцию u, заданную на множестве целых неотрицательных чисел и принимающую значения в поле. Последовательность u называют линейной рекуррентной последовательностью (ЛРП) порядка m ˃ 0 над полем Р, если существуют константы f0,…,f m-1 ∈ P такие, что
ЛРП реализуется схемой линейного регистра сдвига по рисунку. В очередном такте работы регистра значения, содержащиеся в ячейках накопителя, умножаются на соответствующие коэффициенты (hj) и суммируются, после чего происходит сдвиг информации в регистре. В освободившуюся крайнюю ячейку записывается вычисленное значение суммы.
Равенство, устанавливающее зависимость между членами ЛРП, называют законом рекурсии. Многчлен
-характеристический многочлен ЛРП u.
Рисунок. Схема линейного регистра сдвига.
Характеристический многочлен, имеющий наименьшую степень, называется её минимальным многочленом, а степень минимального многочлена – линейной сложностью ЛРП. Линейная сложность определяет минимальную длину ЛРС. Периодом ЛРП называется наименьшее натуральное число t, для которого существует натуральное
Если Р конечное поле из q элементов, максимальное значение периода ЛРП порядка m равно qm -1. Последовательности с максимально возможным периодом называются ЛРП максимального периода или максимальными ЛРП. Закон рекурсии даёт удобный способ вычисления очередного символа ЛРП через предыдущие, но её свойства удобнее изучать с помощью формулы общего члена последовательности. Формула представляет собой аналитическое выражение члена последовательности в виде функции от его номера. Если
неприводимый многочлен над полем Р степени m,
тогда для ЛРП {u(i)} с этим характеристическим многочленом существует единственная константа, а
где
отображение поля ЛРП позволяют обеспечить ряд требований, предъявляемых к псевдослучайным последовательностям. За счёт выбора закона рекурсии можно гарантировать достаточную величину периода и её хорошие статистические свойства. Но аналитическое строение ЛРП оказывается простым. Для определения начального вектора по некоторому отрезку последовательности достаточно решить систему линейных уравнений. Поэтому для использования ЛРП в криптографических приложениях необходимы дополнительные алгоритмы их аналитического усложнения. Алгоритм Берлекэмпа — Мэсси. Эффективным методом нахождения линейногорегистра сдвига минимальной длины, генерирующего заданную последовательность, является алгоритм Берлекэмпа — Мэсси. Пусть - P некоторое поле, e - единица поля. Обозначим
начальный отрезок произвольной последовательности u.
Говорят, что многочлен
вырабатывает отрезок
то есть данный отрезок последовательности является отрезком некоторой ЛРП с характеристическим многочленом G(x). Алгоритм Берлекэмпа — Мэсси строит многочлен наименьшей степени, вырабатывающий этот отрезок. Определим операцию умножения последовательности на многочлен.
где многочлен
и последовательность Многочлен степени m вырабатывает
первые Введём параметры:
Построим последовательность многочленов неубывающих степеней G0(x), G1(x),….. Начальные условия: G0(x) = e, m0 =0. Этап 1. Если
то полагаем
Если Этап t+1. Пусть многочлены G0(x),…..Gt уже построены и степень многочлена
Определим число s=s(t),чтобы
Примем
Если
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.119.199 (0.066 с.) |
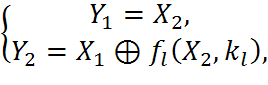
 – совокупность из r биекций множества А;
– совокупность из r биекций множества А;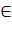 K – выбранный ключ зашифрования;
K – выбранный ключ зашифрования;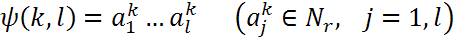 – распределитель.
– распределитель. , где
, где 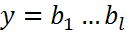 и
и 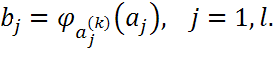
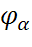 и отображения
и отображения 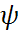 , задающего распределитель.
, задающего распределитель.
 - некоторая функция от
- некоторая функция от 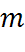 переменных.
переменных.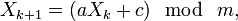
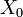 и при разных его значениях получаются различные последовательности случайных чисел. В то же время, многие свойства этой последовательности определяются выбором коэффициентов в формуле и не зависят от выбора стартового числа.
и при разных его значениях получаются различные последовательности случайных чисел. В то же время, многие свойства этой последовательности определяются выбором коэффициентов в формуле и не зависят от выбора стартового числа. ,
, , то они удовлетворяют системе уравнений:
, то они удовлетворяют системе уравнений: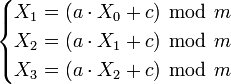
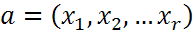
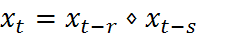
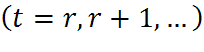 ,
,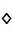 символ бинарной операции: +, -, *, ⊕.
символ бинарной операции: +, -, *, ⊕. могут быть целыми числами или вещественными числами. Для (*) - нечётные числа. Для (⊕) – двоичные числа.
могут быть целыми числами или вещественными числами. Для (*) - нечётные числа. Для (⊕) – двоичные числа.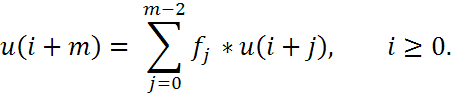
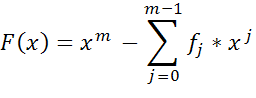
 > 0 такое, что для всех i
> 0 такое, что для всех i  справедливо равенство
справедливо равенство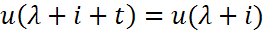 .
.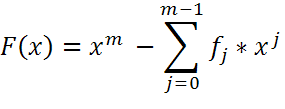
 - его корень в поле
- его корень в поле  ,
, Р такая, что
Р такая, что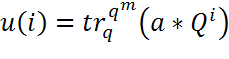 ,
, 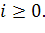

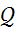 в поле Р.
в поле Р.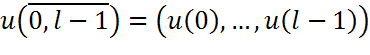
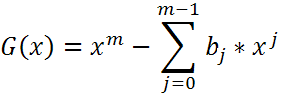
 , если
, если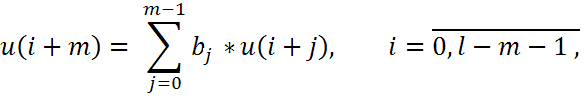
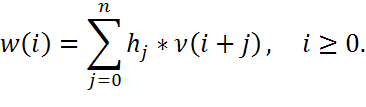

 последовательности u, если
последовательности u, если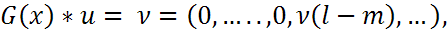
 знаков последовательности равны 0, а следующий за ними отличен от 0.
знаков последовательности равны 0, а следующий за ними отличен от 0. - число знаков последовательности, вырабатываемых многочленом,
- число знаков последовательности, вырабатываемых многочленом,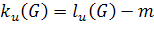 максимальное число первых подряд идущих нулей.
максимальное число первых подряд идущих нулей.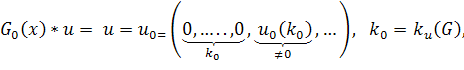
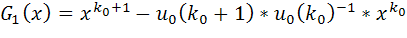 *
*  ,
, 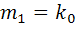 +1.
+1.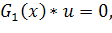 то
то 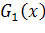 – искомый минимальный многочлен ЛРП. В противном случае строим
– искомый минимальный многочлен ЛРП. В противном случае строим 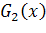 .
. равна mj. Пусть выполняются соотношения
равна mj. Пусть выполняются соотношения
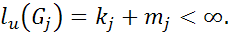
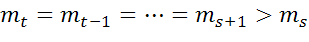 .
.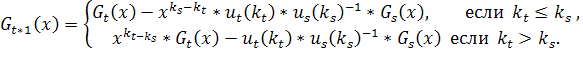
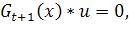 то нужный многочлен построен. В противном случае строим
то нужный многочлен построен. В противном случае строим