Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разработка конечного автоматаСодержание книги
Поиск на нашем сайте
Цель работы - приобретение практических навыков разработки и проектирования конечных автоматов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Краткое теоретическое введение
С помощью конечного автомата, представленного в виде графа, можно реализовать любую регулярную грамматику
G = (N,T,P,S),
где N - множество нетерминальных символов; T - множество терминальных символов; P - множество правил (продукций) грамматики; S - начальное состояние грамматики (начальный нетерминальный символ).
Конечный автомат - это пятерка объектов (K,VT,M,S,Z), где
К - алфавит элементов, называемых состояниями; VT - алфавит, называемый входным алфавитом (символы, которые могут встретиться в цепочке); М - отображение (или функция) множества КхVT во множество К (если М(Q,T) = R, то это означает, что из состояния Q при входном символе Т происходит переключение в состояние R); S - начальное состояние из множества K; Z - непустое множество заключительных состояний из множества К.
Вывод цепочки языка в грамматике интерпретируется на графе как путь от начальной вершины к одной из заключительных, причем для получения самой цепочки нужно выписать все символы, помечающие пройденные дуги в порядке их прохождения. Если в процессе вывода цепочки языка для текущего символа нет дуг, помеченных данным символом, то это означает, что цепочка не входит в язык, и процедура закончена. Если по исчерпании символов цепочки оказывается, что достигнута конечная вершина, то процедура закончена и цепочка входит в язык.
Пример
Рассмотрим регулярную грамматику G = (N,T,P,S)
S::= A0|B1 A::= S1|1 B::= S0|0
Порождаемый данной грамматикой язык состоит из последовательностей, образуемых парами 01 или 10, т.е.
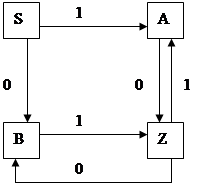
Данной грамматике G соответствует конечный автомат с состояниями S,A,B,Z, где S - начальное состояние; Z - конечное состояние.
Граф для конечного автомата представлен на рис. 1.1.
Рис. 1.1
Матрица переходов состояний для данного конечного автомата представлена в табл. 1.1.
Таблица 1.1
Например, цепочка "10010110" входит в язык, а цепочка "110110" - нет.
ЗАДАНИЕ
Разработать конечный автомат, заданный матрицей переходов состояний, осуществить программную реализацию на заданном преподавателем языке и тестирование.
Примечание. Тестирование должно предусматривать как успешное распознавание входной цепочки, так и неуспешное с выводом соответствующих сообщений вследствие следующих причин: неверный алфавит, отсутствие дуги для перехода, недостижение конечного состояния, пустая цепочка.
СОДЕРЖАНИЕ ОТЧЕТА Отчет о выполнении лабораторной работы должен содержать: · титульный лист; · задание; · граф для конечного автомата; · укрупненную схему программы; · листинг программы; · результаты тестирования; · выводы по выполненной работе.
ВАРИАНТЫ ЗАДАНИЙ
Варианты заданий представлены в табл. 1.2.
Таблица 1.2
ЛАБОРАТОРНАЯ РАБОТА № 2 Разработка детерминированного конечного автомата Цель работы - приобретение практических навыков детерминирования конечных автоматов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.104.140 (0.009 с.) |

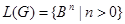 , где B = {01, 10}.
, где B = {01, 10}.